(2.1)
With replacement:
$\Omega=\set{(r,r),(r,g),(r,b),(g,r),(g,g),(g,b),(b,r),(b,g),(b,b)}$
$\norm{\Omega}=3^2$
Without replacement:
If we select the red marble on the first draw, then we cannot select the red marble on the second draw. Hence $(r,r)$ is not in the sample space. Similarly $(g,g)$ and $(b,b)$ are not in the sample space. Hence
$\Omega=\set{(r,g),(r,b),(g,r),(g,b),(b,r),(b,g)}$
$\norm{\Omega}=3\wts2=3!$
(2.2)
Let $X_i$ denote the event that rolls $1$ through $i-1$ were less than $6$ and roll $i$ was $6$.
$$ \Omega=\Bset{X_1,X_2,\dots}=\bigcup_{i=1}^{\infty}X_i $$
(2.3)
$EF=\set{(1,2),(1,4),(1,6),(2,1),(4,1),(6,1)}$
$FG=\set{(1,4),(4,1)}$
$EF^c=\set{(3,2),(3,4),(3,6),(2,3),(4,3),(6,3),(5,2),(5,4),(5,6),(2,5),(4,5),(6,5)}$
$EFG=FG$
(2.5.a)
$2^5$
(2.5.b)
$W=\set{(11000),(11100),(11010),(11001),(11110),(11101),(11011)}$
$\bigcup\set{(00110),(10110),(01110),(00111),(01111),(10111),(11110)}$
$\bigcup\set{(10101)}$
(2.5.c)
$2^3$
(2.5.d)
$AW=\set{(11000),(11100)}$
(2.7.a)
$(2\wts3)^{15}$
(2.7.b)
The count that none of them are blue-collar is $3^{15}$. So the count that at least $1$ is blue-collar is $6^{15}-3^{15}$.
(2.7.c)
$(2\wts2)^{15}$
(2.8.a)
$\pr{A\cup B}=\pr{A}+\pr{B}=0.8$
(2.8.b)
Since $AB=\empty$, then $A$ is a subset of $B^c$. Hence
$\pr{AB^c}=\pr{A}=0.3$
(2.8.c)
$\pr{AB}=\pr\empty=0$
(2.9)
Let $A$ denote the event that a customer carries AmEx. Let $V$ denote the event that a customer carries Visa. Then the event that the customer carries a credit card that the establishment will accept is $A\cup V$.
$$ \pr{A\cup V}=\pr{A}+\pr{V}-\pr{AV}=0.24+0.61-0.11=0.74 $$
(2.10.a)
$$ \pr{R\cup N}=1-\prt{chosen student wears neither}=1-0.6=0.4 $$
(2.10.b)
$$ \pr{RN}=\pr{R}+\pr{N}-\pr{R\cup N}=0.2+0.3-0.4=0.1 $$
(2.11.a)
$$ \pr{A\cup B}=0.28+0.07-0.05=0.3 $$
$$ \prt{neither}=1-\pr{A\cup B}=0.7 $$
(2.11.b)
$A^cB=B-AB$. Venn Diagram makes this clear. And I guess $\pr{B-AB}=\pr{B}-\pr{AB}$.
$0.07-0.05=0.02$
(2.12.a)
$$ \prt{student in at least 1 lang class} $$
$$ =\prt{S}+\prt{F}+\pr{G}-\bop\pr{SF}+\pr{SG}+\pr{FG}\bcp+\pr{SFG} $$
$$ =0.28+0.26+0.16-\bop0.12+0.04+0.06\bcp+0.02 $$
$$ =0.5 $$
So the $\prt{student in no lang class}=1-0.5=0.5$
(2.12.b)
Use the Venn Diagram below to get the answer $\frac{32}{100}$:
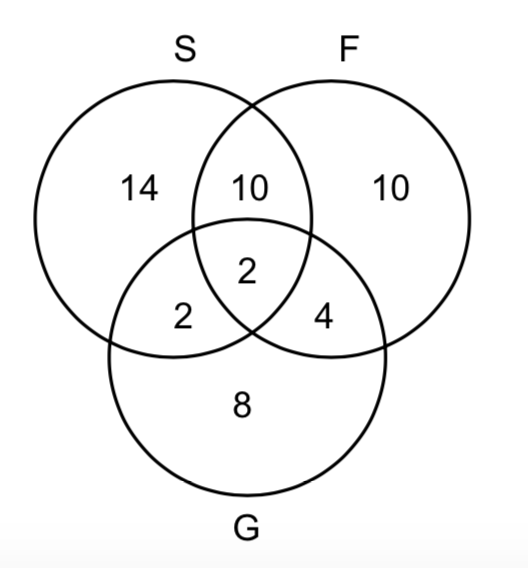
(2.12.c)
Since 50 students are taking at least 1 class and 50 are not, then there $\binom{50}1\binom{50}1$ combinations where exactly $1$ of the $2$ chosen students is taking a lang class and there are $\binom{50}2$ combinations where both are taking a lang class. Hence the probability that at least $1$ of them is taking a lang class is
$$ \frac{\binom{50}1\binom{50}1+\binom{50}2}{\binom{100}2} $$
In [1075]: (binom(50,1)*binom(50,1)+binom(50,2))/binom(100,2)
Out[1075]: 149/198
In [1076]: 149/198
Out[1076]: 0.7525252525252525
Notice that this is a hypergeometric random variable withOUT replacement. Its binomial approximation is
$$ \binom21.5^1(1-.5)^1+\binom22.5^2(1-.5)^0=2\wts\frac14+\frac14=\frac34 $$
We could get more accurate:
- $p_1=\frac12$
- $p_2=\frac{50}{99}$ or $p_2=\frac{49}{99}$
In [260]: p1,p2,p3=1/2,50/99,49/99
In [261]: binom(2,1)*p1*p2+p1*p3
Out[261]: 0.752525252525253
(2.13.a)
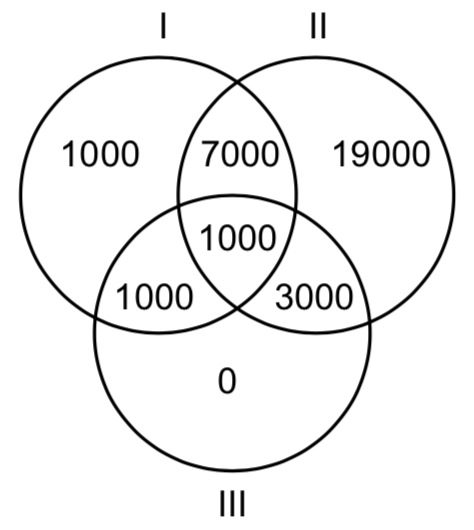
$I+II+III=1+19+0=20$
(2.13.b)
$1+1+3+7=12$
(2.13.c)
$(I\cup III)II=1+3+7=11$
(2.13.d)
$100-(1+1+7+1+3+19)=100-(13+19)=68$
(2.13.e)
$(I\cap II-I\cap II\cap III)\cup(III\cap II-I\cap II\cap III)=3+7=10$
(2.15.a) Flush
Pick a suit and for each suit pick, pick 5 cards
$$ \frac{\binom41\binom{13}5}{\binom{52}5} $$
(2.15.b) Pair
Pick a denomination, pick 2 of the 4 in that denomination, pick 3 denominations from the remaining 12, pick 1 card from each of the 4 cards in each of those denominations
$$ \frac{13\binom{4}2\binom{12}3\binom{4}1\binom{4}1\binom{4}1}{\binom{52}5} $$
Notice that we compute $\binom{12}3\binom{4}1\binom{4}1\binom{4}1$ for the last $3$ cards, rather than $\binom{48}3$. The reason is that we need to avoid picking another pair or picking three of a kind.
(2.15.c) Two Pair
$$ \frac{\binom{13}{2}\binom42\binom42\binom{44}1}{\binom{52}5} $$
Notice the we compute $\binom{13}{2}\binom42\binom42$ for the two pair, rather than $\binom{13}1\binom42\binom{12}1\binom42$. Note that $\binom{13}2=\frac{13\wts12}2$ whereas $\binom{13}1\binom{12}1=13\wts12$. The former avoids permutation dups of denominations. The latter would double count the four cards $7,7,Q,Q$ and $Q,Q,7,7$.
(2.15.d) Three of a Kind
$$ \frac{13\binom{4}3\binom{12}2\binom{4}1\binom{4}1}{\binom{52}5} $$
(2.15.e) Four of a Kind
$$ \frac{13\binom{48}1}{\binom{52}5} $$
Example 5g Full House
$$ \frac{13\binom4312\binom42}{\binom{52}5} $$
Notice that we do want permutation dups of denominations now. That is, the hand $Q,Q,Q,7,7$ is different from $7,7,7,Q,Q$.
Example 5f Straight
To get any combination of $A,2,3,4,5$, the count is $4^5$. The total number of ways to get a straight flush from these combinations is $4$ (there is exactly $1$ way to get a straight flush of spades starting with an ace, etc). So the total number of combinations of straights starting with an ace and excluding a straight flush is $4^5-4$.
Now we can get a straight starting with $A,2,3,4,5,6,7,8,9,10$. For instance $10,J,Q,K,A$. That’s a count of 10.
The total count is (number of starting points) $\times$ (number of combos at each starting point) $=10(4^5-4)$.
$$ \frac{10(4^5-4)}{\binom{52}5} $$
Straight Flush
$$ \frac{10\wts4}{\binom{52}5} $$
(2.16.a)
Note that $1,2,3,4,5$ is NOT the same as $2,1,3,4,5$. So we want to compute permutations (not combinations) of no two alike. There are $6^5$ permutations of the $5$ dice.
We want to get $5$ different numbers from $5$ dice. Since there are $\binom65$ ways to choose $5$ different numbers from $1$ to $6$, and $5!$ different orderings for each selection of $5$ distinct numbers, then we have $\wNt{no two alike}$ $=\binom65\wts5!=6!$ and
$$ \prt{no two alike}=\frac{6!}{6^5} $$
In [1129]: wf(6)/pw(6,5)
Out[1129]: 0.092592592592592587
(2.16.b)
There are $6$ ways to chose the denomination that will be a pair. For each of these choices, there are $5$ dice from which to choose $2$ to assign the chosen denomination. But the number of dice permutations for assigning the chosen denomination is not $5\wts4$. For example, if the chosen denomination is $1$, then we could assign a $1$ to die $1$ and assign a $1$ to die $2$. Or we could reverse that. But the reverse is the same permutation:
- 1,1,2,3,4
- 1,1,2,3,4
So the number of ways we can assign $1$ and $1$ is $\frac{5\wts4}2=\binom52$. And the number of ways we can choose a pair denomination and assign that to two dice is $6\binom52$.
For the other three dice, we must select $3$ denominations from the remaining $5$. That is $\binom53$. Then we can assign each denomination to any of the remaining $3$ dice. That is $3!$. So this count is $\binom533!=5\wts4\wts3$.
Hence the desired probability is
$$ \prt{one pair}=\frac{6\wts\binom52\wts5\wts4\wts3}{6^5} $$
In [1143]: from sympy import N
In [1144]: winom=lambda n,i: N(binom(n,i))
In [1145]: 6*winom(5,2)*5*4*3/pw(6,5)
Out[1145]: 0.462962962962963
(2.16.c)
We first choose which two numbers will be pairs $\binom62$, then choose which dice will be pairs $\binom52\binom32$. Notice that $\binom62$ will count $(1,2)$ but not $(2,1)$. That’s a potential problem because we want different pairs to be assigned to all the different dice. But $\binom52\binom32$ will ensure that this occurs. And then choose one remaining number from $4$ choices. So
$$ \prt{two pair}=\frac{\binom62\binom52\binom324}{6^5} $$
In [1156]: winom(6,2)*winom(5,2)*winom(3,2)*4/pw(6,5)
Out[1156]: 0.231481481481481
(2.16.d)
We choose which number is three-alike $\binom61=6$, then choose which dice will be three-alike $\binom53$, then choose which $2$ numbers will be unalike $\binom52$, and finally choose which dice will be unalike $2!=2$.
$$ \prt{three alike}=\frac{6\binom53\binom522}{6^5} $$
In [1160]: 6*winom(5,3)*winom(5,2)*2/pw(6,5)
Out[1160]: 0.154320987654321
(2.16.e)
We want to be careful with permutations. In problem (2.16.c), the case of two-pair, we were careful to avoid permutation dups. But now we want them. In the case of regular poker (Example 5g Full House), we wanted the perm dup of $7,Q$ and $Q,7$ for the case of a full house. It’s the same thing here.
We choose which number is three alike $\binom61$, then choose which dice are three alike $\binom53$, and then choose which number is two alike $\binom51$. Notice how this solution differs from (2.16.c).
$$ \prt{full house}=\frac{\binom61\binom53\binom51}{6^5} $$
In [1163]: winom(6,2)*winom(5,3)*2/pw(6,5)
Out[1163]: 0.0385802469135802
(2.16.f)
We choose which number is four alike $\binom61=6$, choose which dice are four alike $\binom54$, and choose a number $\binom51=5$ for the remaining die.
$$ \prt{four alike}=\frac{6\binom545}{6^5} $$
In [1165]: 6*winom(5,4)*5/pw(6,5)
Out[1165]: 0.0192901234567901
(2.16.g)
We choose which number is five alike $\binom61=6$.
$$ \prt{five alike}=\frac{6}{6^5} $$
In [1169]: 1/pw(6,4)
Out[1169]: 0.0007716049382716049
(2.18)
Count of ways to get Black Jack with ace first: $4\wts16$
Count of ways to get Black Jack with ace second: $16\wts4$
$$ \frac{4\wts16+16\wts4}{52\wts51}=\frac{4\wts16\wts2}{52\wts51} $$
In [1187]: (4*16*2)/(52*51)
Out[1187]: 0.048265460030165915
Or we can do this with permutations:
$$ \frac{\binom41\binom{16}1}{\binom{52}2} $$
In [278]: winom(4,1)*winom(16,1)/winom(52,2)
Out[278]: 0.0482654600301659
(2.19)
Count of red rolls: $2\wts2$: $\set{(r_1,r_1),(r_1,r_2),(r_2,r_1),(r_2,r_2)}$
Count of black rolls: $2\wts2$: $\set{(b_1,b_1),(b_1,b_2),(b_2,b_1),(b_2,b_2)}$
Count of yellow rolls: $1\wts1$: $\set{(y,y)}$
Count of white rolls: $1\wts1$: $\set{(w,w)}$
$$ \frac{10}{6\wts6}=\frac5{18} $$
(2.20)
$$ \prt{neither of us gets a blackjack}=1-\prt{at least one of us gets a blackjack} $$
$$ \prt{at least one of us gets a blackjack} $$
$$ =\pr{A\cup B}=\pr{A}+\pr{B}-\pr{AB} $$
$$ =\frac{2\wts4\wts16}{52\wts50}+\frac{2\wts4\wts16}{51\wts49}-\frac{2\wts4\wts16\wts2\wts3\wts15}{52\wts51\wts50\wts49} $$
Note that the solutions manual has a misprint on this one. The plus should be a minus. With this corrected, my answer is still slightly different from the solutions manual. My answer assumes that the deal goes: a card to me, a card to the dealer, a card to me, and a card to the dealer.
I think to really handle this correctly, you need to condition $B$ on the cases that $A$ gets $x$ number of aces or $y$ number of $10,J,Q,K$.
Now what if we handle this with combinations instead of permutations and assume that the goes as the solutions manual expects:
$$ \frac{2\binom41\binom{16}1}{\binom{52}2}-\frac{\binom{4}2\binom{16}2}{\binom{52}4} $$
$$ =\frac{2\wts2\wts4\wts16}{52\wts51}-\frac{\frac{4\wts3}{2!}\frac{16\wts15}{2!}}{\frac{52\wts51\wts50\wts49}{4!}} $$
$$ =\frac{4\wts4\wts16}{52\wts51}-\frac{4!\frac{4\wts3}{2!}\frac{16\wts15}{2!}}{52\wts51\wts50\wts49} $$
$$ =\frac{4\wts4\wts16}{52\wts51}-\frac{3!\wts4\wts3\wts16\wts15}{52\wts51\wts50\wts49} $$
So this is a bit different from the corrected solutions manual answer. I guess permutations is the way to handle this?
(2.21.a)
Let $X$ denote the number of the children in the chosen family:
$$ \prt{X=1}=\frac4{20}=\frac15 $$
$$ \prt{X=2}=\frac8{20}=\frac25 $$
$$ \prt{X=3}=\frac5{20}=\frac14 $$
$$ \prt{X=4}=\frac2{20}=\frac1{10} $$
$$ \prt{X=5}=\frac1{20} $$
(2.21.b)
$$ 4\wts1+8\wts2+5\wts3+2\wts4+5=20+15+13=48 $$
Let $Y$ denote the number of children in the family of the chosen child:
$$ \prt{Y=1}=\frac4{48} $$
$$ \prt{Y=2}=\frac{2\wts8}{48} $$
$$ \prt{Y=3}=\frac{3\wts5}{48} $$
$$ \prt{Y=4}=\frac{4\wts2}{48} $$
$$ \prt{Y=5}=\frac{5\wts1}{48} $$
(2.22)
The only way for the post-ordering to be the same as the initial ordering is if there exists some $k$, $0\leq k\leq n$, such that the first $k$ flips are all heads and the last $n-k$ flips are all tails. There are $n+1$ such outcomes. For instance:
$F_4=\set{(t,t,t,t),(h,t,t,t),(h,h,t,t),(h,h,h,t),(h,h,h,h)}$
$F_5=\set{(t,t,t,t,t),(h,t,t,t,t),(h,h,t,t,t),(h,h,h,t,t),(h,h,h,h,t),(h,h,h,h,h)}$
$$ \prt{same ordering}=\frac{n+1}{2^n} $$
(2.23)
There are $6^2=36$ possible rolls. Of these, exactly $6$ rolls consist of equal lands. So there are $15$ rolls where the second lands on a higher value. Hence the desired probability is $\frac{15}{36}=\frac5{12}$.
(2.24)
$\pr{X=2}=\frac{1}{36}\dq\set{(1,1)}$
$\pr{X=3}=\frac{2}{36}\dq\set{(1,2),(2,1)}$
$\pr{X=4}=\frac{3}{36}\dq\set{(1,3),(3,1),(2,2)}$
$\pr{X=5}=\frac{4}{36}\dq\set{(1,4),(4,1),(2,3),(3,2)}$
$\pr{X=6}=\frac{5}{36}\dq\set{(1,5),(5,1),(2,4),(4,2),(3,3)}$
$\pr{X=7}=\frac{6}{36}\dq\set{(1,6),(6,1),(2,5),(5,2),(3,4),(4,3)}$
$\pr{X=8}=\frac{5}{36}\dq\set{(2,6),(6,2),(3,5),(5,3),(4,4)}$
$\pr{X=9}=\frac{4}{36}\dq\set{(3,6),(6,3),(4,5),(5,4)}$
$\pr{X=10}=\frac{3}{36}\dq\set{(4,6),(6,4),(5,5)}$
$\pr{X=11}=\frac{2}{36}\dq\set{(5,6),(6,5)}$
$\pr{X=12}=\frac{1}{36}\dq\set{(6,6)}$
(2.25)
Let $E$ denote the event that a $5$ appears first. Let’s show that $E=\bigcup_{n=1}^{\infty}E_n$.
First let’s show that the $E_n$ are disjoint. $E_n$ denotes the event that a $5$ or $7$ doesn’t occur on rolls $n-1$. But $E_{n-1}$ denotes the event that a $5$ occurs on the roll $n-1$. Hence they are mutually exclusive and
$$ \prB{\bigcup_{n=1}^{\infty}E_n}=\sum_{n=1}^{\infty}\pr{E_n} $$
Now suppose $x\in \bigcup_{n=1}^{\infty}E_n$. Then $x\in E_n$ for some $n$. Hence no $5$ or $7$ appeared on rolls $1$ through $n-1$ and a $5$ appeared on roll $n$. Hence a $5$ appeared before a $7$. Hence $x\in E$.
Conversely, suppose $x\in E$. Then for some $n$, rolls $1$ through $n-1$ did not sum to $5$ or $7$ and roll $n$ summed to $5$. Hence $x\in E_n\subset E$.
Hence $E=\bigcup_{n=1}^{\infty}E_n$ and
$$ \pr{E}=\prB{\bigcup_{n=1}^{\infty}E_n}=\sum_{n=1}^{\infty}\pr{E_n} $$
Now let’s look at $E_n$. There are $36^n$ possible ways to roll $2$ dice $n$ times. There are $(36-(4+6))^{n-1}=26^{n-1}$ possible ways to roll anything but a $5$ or $7$ on the first $n-1$ rolls. And there are $4$ ways to roll a $5$ on the $n^{th}$ roll.
$$ \pr{E_n}=\frac{26^{n-1}4}{36^n}=\frac4{36}\frac{26^{n-1}}{36^{n-1}}=\frac19\Bop\frac{26}{36}\Bcp^{n-1}=\frac19\Bop\frac{13}{18}\Bcp^{n-1} $$
Alternatively, we can view this as a binomial random variable. For a given roll, the probability that the sum is not $5$ or $7$ is $1-\frac{10}{36}=\frac{26}{36}=\frac{13}{18}\equiv p$.
The probability that the first $n-1$ rolls do not sum to $5$ or $7$ is:
$$ \binom{n-1}{n-1}p^{n-1}(1-p)^{n-1-(n-1)}=p^{n-1}=\Bop\frac{13}{18}\Bcp^{n-1} $$
The probability that the $n^{th}$ roll sums to $5$ is $\frac4{36}=\frac19$. Hence
$$ \pr{E_n}=\frac19\Bop\frac{13}{18}\Bcp^{n-1} $$
And
$$ \pr{E}=\sum_{n=1}^{\infty}\pr{E_n}=\sum_{n=1}^{\infty}\frac19\Bop\frac{13}{18}\Bcp^{n-1}=\frac19\sum_{n=1}^{\infty}\Bop\frac{13}{18}\Bcp^{n-1} $$
$$ =\frac19\sum_{j=0}^{\infty}\Bop\frac{13}{18}\Bcp^{j}=\frac19\frac1{1-\frac{13}{18}}=\frac19\frac1{\frac{5}{18}}=\frac19\frac{18}5=\frac25 $$
(2.25.b)
For a given roll, the probability that the sum is not $4$ or $7$ is $1-\frac{9}{36}=\frac{27}{36}=\frac34\equiv p$.
The probability that the first $n-1$ rolls do not sum to $4$ or $7$ is:
$$ p^{n-1}=\Bop\frac{3}{4}\Bcp^{n-1} $$
The probability that the $n^{th}$ roll sums to $4$ is $\frac3{36}=\frac1{12}$.
$$ \pr{E_n}=\frac1{12}\Bop\frac{3}{4}\Bcp^{n-1} $$
$$ \sum_{n=1}^{\infty}\pr{E_n}=\frac1{12}\sum_{j=0}^{\infty}\Bop\frac{3}{4}\Bcp^{j}=\frac1{12}\frac1{1-\frac{3}{4}}=\frac1{12}\frac1{\frac{1}{4}}=\frac1{12}\frac{4}{1}=\frac1{3} $$
(2.25.c)
For a given roll, the probability that the sum is not $6$ or $7$ is $1-\frac{11}{36}=\frac{25}{36}\equiv p$.
The probability that the first $n-1$ rolls do not sum to $6$ or $7$ is:
$$ p^{n-1}=\Bop\frac{25}{36}\Bcp^{n-1} $$
The probability that the $n^{th}$ roll sums to $6$ is $\frac5{36}$.
$$ \pr{E_n}=\frac5{36}\Bop\frac{25}{36}\Bcp^{n-1} $$
$$ \sum_{n=1}^{\infty}\pr{E_n}=\frac5{36}\sum_{j=0}^{\infty}\Bop\frac{25}{36}\Bcp^{j}=\frac5{36}\frac1{1-\frac{25}{36}}=\frac5{36}\frac1{\frac{11}{36}}=\frac5{36}\frac{36}{11}=\frac5{11} $$
(2.25.d) in preparation for problem 26
For $n>1$, let $E_{4,n}$ denote the event that the first and $n^{th}$ rolls are $4$ and that rolls $2$ through $n-1$ are not $4$ or $7$. Let $E_{4,1}$ denote the empty set.
For a given roll, the probability that the sum is not $4$ or $7$ is $1-\frac{9}{36}=\frac{27}{36}=\frac34\equiv p$.
The probability that the second through $n-1$ rolls do not sum to $4$ or $7$ is:
$$ p^{n-2}=\Bop\frac{3}{4}\Bcp^{n-2} $$
The probability that the $n^{th}$ roll sums to $4$ is $\frac3{36}=\frac1{12}$.
$$ \pr{E_{4,1}}=0\dq\pr{E_{4,n}}=\Bop\frac1{12}\Bcp^2\Bop\frac{3}{4}\Bcp^{n-2} $$
$$ \sum_{n=1}^{\infty}\pr{E_{4,n}}=\Bop\frac1{12}\Bcp^2\sum_{n=2}^{\infty}\Bop\frac{3}{4}\Bcp^{n-2} $$
$$ =\Bop\frac1{12}\Bcp^2\sum_{j=0}^{\infty}\Bop\frac{3}{4}\Bcp^{j} $$
$$ =\Bop\frac1{12}\Bcp^2\frac1{1-\frac{3}{4}}=\Bop\frac1{12}\Bcp^2\frac1{\frac{1}{4}}=\frac1{12}\frac1{12}\frac{4}{1}=\frac1{12}\frac13 $$
$$ =\prt{first roll is 4}\sum_{n=1}^{\infty}\pr{F_n} $$
where $F_n$ denotes the event that a $4$ occurs on the $n^{th}$ roll and no $4$ or $7$ occurs on the first $n-1$ rolls. We proved in problem (2.25.b) that $\sum_{n=1}^{\infty}\pr{F_n}=\frac13$.
(2.26)
First note that the sets $E_i,2\leq i\leq12$ are mutually exclusive. Let $E$ denote the event that the player wins. Note that if a player wins, his first roll must be one of $2,3,\dots,11,12$. Hence the sets $E_i,2\leq i\leq12$ are mutually exhaustive of $E$. That is $E=\bigcup_{i=2}^{12}E_i$.
Hence if a players wins, exactly $1$ of the events $E_i$ must occur and
$$ \pr{E}=\sum_{i=2}^{12}\pr{E_i} $$
Note that $E_2$ is the event that the initial dice sum is $2$ and the player wins. But this intersection is the empty set. The same goes for $E_3$ and $E_{12}$. Hence
$$ 0=\pr{E_2}=\pr{E_3}=\pr{E_{12}} $$
Similarly note that
$$ 0=\pr{E_{2,n}}=\pr{E_{3,n}}=\pr{E_{12,n}}\text{, for all }n\geq1 $$
since, if the initial sum is $2$, $3$, or $12$, the player loses. Hence
$$ \pr{E_{i}}=\sum_{n=1}^{\infty}\pr{E_{i,n}}=0\text{, for }i=2,3,12 $$
Also note that $E_7$ is the event that the initial dice sum is $7$ and the player wins. Similarly for $E_{11}$. But the player wins if the initial roll is $7$ or $11$. Also note that if the initial sum is $7$ or $11$, there is no $n^{th}$ roll for $n>1$. Hence
$$ \pr{E_7}=\pr{E_{7,1}}\dq\pr{E_{7,n}}=0\text{, for all }n>1\dq\pr{E_7}=\sum_{i=n}^{\infty}\pr{E_{7,n}} $$
$$ \pr{E_{11}}=\pr{E_{11,1}}\dq\pr{E_{11,n}}=0\text{, for all }n>1\dq\pr{E_{11}}=\sum_{i=n}^{\infty}\pr{E_{11,n}} $$
Thus we have shown
$$ \pr{E_{i}}=\sum_{n=1}^{\infty}\pr{E_{i,n}}\text{, for }i=2,3,7,11,12 $$
But also note that $\settx{initial sum is 7}\subset\settx{win}$. Hence
$$ \settx{initial sum is 7 and win}=\settx{initial sum is 7} $$
and
$$ \pr{E_{7}}=\prt{initial sum is 7 and win}=\prt{initial sum is 7}=\frac6{36} $$
Similarly
$$ \pr{E_{11}}=\prt{initial sum is 11 and win}=\prt{initial sum is 11}=\frac2{36} $$
Now let’s consider the event $E_4$. This event occurs when the player’s initial roll is $4$ and he wins. We know that the probability that the player rolls a $4$ on any given roll is $\frac1{12}$. And we know that $\pr{E_{4,1}}=0$. We can also see that
$$ \pr{E_{4,2}}=\prt{roll 1 is 4, roll 2 is 4}=\prt{roll 1 is 4}\prt{roll 2 is 4} $$
Similarly, for $n>2$, we have
$$ \pr{E_{4,n}}=\prt{roll 1 is 4, rolls 2 thru $n-1$ are not $4$ or $7$, roll n is 4} $$
$$ =\prt{roll 1 is 4}\prt{rolls 2 thru $n-1$ are not $4$ or $7$}\prt{roll n is 4} $$
But in problem (2.25.d), we proved that
$$ \sum_{n=1}^{\infty}\pr{E_{4,n}}=\frac{1}{12}\frac{1}{3}=\frac{1}{36} $$
And it’s easy to see that $\pr{E_{4}}=\sum_{n=1}^{\infty}\pr{E_{4,n}}$.
Similarly we can show that
$$ \pr{E_{5}}=\sum_{n=1}^{\infty}\pr{E_{5,n}}=\frac19\frac25=\frac{2}{45} $$
$$ \pr{E_{6}}=\sum_{n=1}^{\infty}\pr{E_{6,n}}=\frac{5}{36}\frac{5}{11}=\frac{25}{396} $$
It is easy to see that
$$ \pr{E_{10}}=\pr{E_{4}}\dq\pr{E_{9}}=\pr{E_{5}}\dq\pr{E_{8}}=\pr{E_{6}} $$
Thus
$$ \pr{E}=\sum_{i=2}^{12}\pr{E_i} $$
$$ =2\pr{E_4}+2\pr{E_5}+2\pr{E_6}+\pr{E_7}+\pr{E_{11}} $$
$$ =2\frac1{36}+2\frac2{45}+2\frac{25}{396}+\frac6{36}+\frac2{36} $$
In [1197]: 2*(1/36)+2*(2/45)+2*(25/396)+8/36
Out[1197]: 0.4929292929292929
(2.27)
Let $A_i$ denote the event that player $A$ selects the red ball on his $i^{th}$ pick. Let $R_A$ denote the event that player $A$ selects the red ball. Then
$$ R_A=\bigcup_{i=1}^{4}A_i \tag{2.27.1} $$
and
$$ \pr{R_A}=\sum_{i=1}^{4}\pr{A_i} \tag{2.27.2} $$
2.27.2 follows because the $\set{A_i}$ are mutually exclusive.
$$ \pr{R_A}=\frac3{10}+\frac7{10}\frac69\frac38+\frac7{10}\frac69\frac58\frac47\frac36+\frac7{10}\frac69\frac58\frac47\frac36\frac25\frac34 $$
In [1202]: 3/10+(7/10)*(6/9)*(3/8)+(7/10)*(6/9)*(5/8)*(4/7)*(3/6)+(7/10)*(6/9)*(5/8)*(4/7)*(3/6)*(2/5)*(3/4)
Out[1202]: 0.5833333333333334
(2.28.without.replacement)
Let $R$, $B$, $G$ denote the events that the selected 3 are all red, blue, and green. Let $A$ denote the event that the selected 3 are all of the same color. Then the $R$, $B$, $G$ are mutually exclusive and exhaustive in $A$. Hence
$$ \pr{A}=\pr{R}+\pr{B}+\pr{G} $$
$$ =\frac{5\wts4\wts3}{19\wts18\wts17}+\frac{6\wts5\wts4}{19\wts18\wts17}+\frac{8\wts7\wts6}{19\wts18\wts17} $$
In [1239]: (5*4*3+6*5*4+8*7*6)/(19*18*17)
Out[1239]: 0.08875128998968008
Or we can compute combinations instead of permutations:
$$ \frac{\binom53+\binom63+\binom83}{\binom{19}3} $$
In [1243]: (winom(5,3)+winom(6,3)+winom(8,3))/winom(19,3)
Out[1243]: 0.0887512899896801
Different:
$$ \frac{\binom51\binom61\binom81}{\binom{19}3} $$
In [1244]: (5*6*8)/winom(19,3)
Out[1244]: 0.247678018575851
(2.28.with.replacement)
$$ \pr{A}=\frac{5^3+6^3+8^3}{19^3} $$
Different:
In isolation, the probability that the first ball chosen is red is $\frac5{19}$. In isolation, the probability that the second ball chosen is blue is $\frac6{19}$. In isolation, the probability that the third ball chosen is green is $\frac8{19}$. So the probability of drawing the permutation $RGB$ is $\frac{5\wts6\wts8}{19^3}$.
There are $3!$ permutations of $RGB$, each of which is disjoint, each with the same probability. Hence
$$ \prt{all different}=\pr{RGB}+\pr{RBG}+\pr{GRB}+\pr{GBR}+\pr{BRG}+\pr{BGR} $$
$$ =3!\frac{5\wts6\wts8}{19^3} $$
Or we can count it out: there are $5\wts6\wts8$ ways for the permutation $RBG$ to occur. And there are $5\wts6\wts8$ ways for the permutation $RGB$ to occur. Etc. There are $6=3!$ such permutations, all of them disjoint with all others. And the sample space consists of $19^{3}$ items. Hence
$$ \prt{all different}=\frac{\sum_{i=1}^{3!}5\wts6\wts8}{19^3}=3!\frac{5\wts6\wts8}{19^3} $$
(2.29.a)
$$ \frac{\binom{n}2+\binom{m}2}{\binom{n+m}2} $$
Or with permutations:
$$ \frac{n(n-1)+m(m-1)}{(n+m)(n+m-1)} $$
(2.29.b)
$$ \frac{n^2+m^2}{(n+m)^2} $$
(2.29.c)
$$ \frac{n^2+m^2}{(n+m)^2}\geq\frac{n(n-1)+m(m-1)}{(n+m)(n+m-1)} $$
$\iff$
$$ \frac{(n^2+m^2)(n+m-1)}{(n+m)^2(n+m-1)}\geq\frac{\bop n(n-1)+m(m-1)\bcp(n+m)}{(n+m)^2(n+m-1)} $$
$\iff$
$$ (n^2+m^2)(n+m-1)\geq\bop n^2-n+m^2-m\bcp(n+m) $$
$\iff$
$$ n^3+n^2m-n^2+m^2n+m^3-m^2\geq n^3+n^2m-n^2-nm+m^2n+m^3-mn-m^2 $$
$\iff$
$$ 0\geq -nm-mn=-2mn $$
Which is true since $m,n>0$.
(2.30.a)
Total count: $\binom84\binom944!$
Count with Reb and Elise paired: $\binom11\binom73\binom11\binom833!$
$$ \frac{\binom73\binom833!}{\binom84\binom944!} $$
(2.30.b)
Count with Reb and Elise not paired: $\binom11\binom73\binom11\binom83(4!-3!)$
$$ \frac{\binom73\binom83(4!-3!)}{\binom84\binom944!} $$
In [1249]: (binom(7,3)*binom(8,3)*(wf(4)-wf(3)))/(binom(8,4)*binom(9,4)*wf(4))
Out[1249]: 1/6
(2.30.c)
Total count of chosen to represent: $\binom84\binom94$
Count with only Reb chosen to represent: $\binom11\binom73\binom10\binom84$
Count with only Elise chosen to represent: $\binom10\binom74\binom11\binom83$
The solution excludes the count of both chosen to represent, so I guess “either/or” excludes this.
$$ \frac{\binom73\binom84+\binom74\binom83}{\binom84\binom94} $$
In [1251]: (binom(7,3)*binom(8,4)+binom(7,4)*binom(8,3))/(binom(8,4)*binom(9,4))
Out[1251]: 1/2
(2.31.a)
Total count: $3^3$
Complete team count: $3\wts2\wts1$
$$ \frac{3\wts2}{3^3}=\frac{2}{9} $$
Another way to look at it: Count the number of ways we can get $GFC$. There is exactly one way to get this. And there are $3!$ permutations of $GFC$.
(2.31.b)
All same count: $3\wts1\wts1$
$$ \frac{3}{3^3}=\frac{1}{9} $$
Another way to look at it: Count the number of ways we can get $GGG$. There is exactly one way to get this. And there is $1$ permutation of $GGG$. The same goes for $FFF$ and $CCC$. That’s $1+1+1$.
(2.32)
$ \frac{g}{g+b} $
(2.33)
Probability that exactly $2$ of $4$ recaptured are tagged:
$$ \frac{\binom52\binom{15}2}{\binom{20}4}=\frac{70}{323}\approx0.216718266253870 $$
Or we can compute this as a binomial random variable: $p\equiv\frac5{20}=\frac14$
$$ \binom42p^2(1-p)^2=6\frac1{16}\frac9{16}=\frac{54}{256}=0.2109375 $$
We’re assuming that each of the $20$ elk is equally likely to be captured. We’re also assuming no elk deaths or introduced elk.
Notice that our binomial random variable approximation is only accurate to $2$ decimal places. The reason is that this is a problem “withOUT replacement”. That is, $p$ changes slightly after each recapture. For instance, when we computed exactly $2$ tagged, the probabilities were
- $p_1=\frac5{20}$
- $p_2=\frac4{19}$ or $\frac5{19}$
- $p_3=\frac3{18}$ or $\frac4{18}$ or $\frac5{18}$
- $p_4=\frac3{17}$ or $\frac4{17}$
These calculations are precise:
In [1345]: winom(4,2)*(5/20)*(4/19)*(1-3/18)*(1-3/17)
Out[1345]: 0.216718266253870
In [1346]: winom(4,2)*(5/20)*(4/18)*(1-4/19)*(1-3/17)
Out[1346]: 0.216718266253870
In [1347]: (winom(5,2)*winom(15,2))/(winom(20,4))
Out[1347]: 0.216718266253870
(2.34)
$$ \frac{\binom{32}{13}}{\binom{52}{13}} $$
(2.35.a)
$$ \frac{\binom{12}{3}\binom{16}{2}\binom{18}{2}}{\binom{46}{7}} $$
(2.35.b)
$$ \frac{\sum_{i=2}^7\binom{12}{i}\binom{34}{7-i}}{\binom{46}{7}} $$
or
$$ 1-\frac{\sum_{i=0}^1\binom{12}{i}\binom{34}{7-i}}{\binom{46}{7}} $$
In [1267]: wt=[winom(12,i)*winom(34,7-i)/winom(46,7) for i in range(2,8)]
In [1268]: sum(wt)
Out[1268]: 0.597971178902891
In [1269]: wt=[winom(12,i)*winom(34,7-i)/winom(46,7) for i in range(0,2)]
In [1270]: 1-sum(wt)
Out[1270]: 0.597971178902891
(2.35.c)
$$ \frac{\binom{12}7+\binom{16}7+\binom{18}7}{\binom{46}{7}} $$
(2.35.d)
We use the identity $\pr{A\cup B}=\pr{A}+\pr{B}-\pr{AB}$:
$$ \frac{\binom{12}3\binom{34}4+\binom{16}3\binom{30}4-\binom{12}{3}\binom{16}3\binom{18}1}{\binom{46}{7}} $$
(2.36.a)
$$ \frac{\binom42}{\binom{52}2} $$
(2.36.b)
$$ \frac{\binom{13}1\binom42}{\binom{52}2} $$
(2.37.a)
$$ \frac{\binom{7}5}{\binom{10}5}=\frac{7\wts6\wts5\wts4\wts3}{10\wts9\wts8\wts7\wts6}=\frac{5\wts4\wts3}{10\wts9\wts8}=\frac1{2\wts3\wts2}=\frac1{12} $$
(2.37.b)
$$ \frac{\binom{7}4\binom31+\binom{7}5}{\binom{10}5} $$
(2.38)
$$ \frac12=\frac{\binom32}{\binom{n}2}=\frac3{\frac{n(n-1)}2} $$
$$ \frac{n(n-1)}2=6 $$
$$ (n+3)(n-4)=n^2-n-12=0 $$
$\implies n=4$
(2.39)
$$ \frac{5\wts4\wts3}{5^3}=\frac{4\wts3}{25}=\frac{12}{25} $$
Another way to think about this: There are $\binom53$ ways to choose $3$ hotels. Say the choices are $ABC$. There are $3!$ permutations of $ABC$. The same goes for $CDE$ or any choice in the count $\binom53$. Hence the count is $\binom533!=\frac{5\wts4\wts3}{3!}3!=5\wts4\wts3$.
(2.40)
$1$ repairer is called: they can all call $A$, or all call $B$, or all call $C$, or all call $D$:
$$ \frac{4}{4^4}=\frac1{64}=\frac4{256} $$
$2$ repairers are called:
First we choose which two repairers: $\binom42$. We don’t want permutations at this point. We’ll get all necessary permutations in a moment.
Next we notice that there are three disjoint ways that two chosen repairers can be distributed among the $4$ customers. For example, suppose we chose repairers $A$ and $B$. Then we can disjointly have
- $3$ $A$’s and $1$ $B$
- $2$ $A$’s and $2$ $B$’s
- $1$ $A$ and $3$ $B$’s
In the first case, there are $\frac{4!}{3!}=4$ unique permutations (since there are $3$ identical $A$’s). And similarly for the third case. In the second case, there are $\frac{4!}{2!2!}$ unique perumations (since there are $2$ identical $A$’s and $2$ identical $B$’s). Hence the desired probability is
$$ \frac{\binom42\bop4+\frac{4!}{2!2!}+4\bcp}{4^4}=\frac{6\wts14}{4^4}=\frac{21}{64}=\frac{84}{256} $$
$3$ repairers are called:
First we choose which three repairers: $\binom43$.
For each choice of three repairers, exactly one of them must be called twice in a possible permutation. For instance, suppose we chose repairers $A$, $B$, and $C$. Then one possible permutation is $ABCA$. Another is $ABCB$. And a third is $ABCC$. That is, for each choice of three repairers, we must choose one that will be called by two different customers. Hence for each choice of three repairers, we must choose one from three: $\binom31$.
Now for each choice of three repairers, and for each choice of which one of the three is called twice, there are $\frac{4!}{2!}$ unique permutations (since there are $2$ identical). Hence the desired probability is
$$ \frac{\binom43\binom31\frac{4!}{2!}}{4^4}=\frac{4\wts3\wts12}{4^4}=\frac{9}{4^2}=\frac9{16}=\frac{144}{256} $$
$4$ repairers are called:
$$ \frac{\binom444!}{4^4}=\frac{1\wts3!}{4^3}=\frac6{64}=\frac{24}{256} $$
Check:
$$ 4+84+144+24=256 $$
(2.41)
Probability that six comes up exactly zero times:
Total count: $6^4$
Zero count: $5^4$
$$ \frac{5^4}{6^4} $$
$$ \prt{6 appears at least once}=1-\prt{six never appears}=1-\frac{5^4}{6^4} $$
In [1325]: 1-pw(5,4)/pw(6,4)
Out[1325]: 0.51774691358024694
More directly:
$6$ appears once count: $4\wts5^3$
To show this, let’s count the number of ways a $6$ appears only on the the first die: $5^3$. The same goes for the second, third, and fourth dice.
$6$ appears twice count: $\binom425^2$
$6$ appears three times count: $\binom435$
$6$ appears four times count: $1$
$$ \prt{6 appears at least once}=\frac{4\wts5^3+\binom425^2+\binom435+1}{6^4} $$
In [1328]: (4*pw(5,3)+winom(4,2)*pw(5,2)+winom(4,3)*5+1)/pw(6,4)
Out[1328]: 0.517746913580247
In [331]: sum([winom(4,i)*pw(5,4-i)/pw(6,4) for i in range(1,5)])
Out[331]: 0.517746913580247
In [1329]: (4*pw(5,3)+winom(4,2)*pw(5,2)+winom(4,3)*5+1)/pw(6,4)-(1-pw(5,4)/pw(6,4))
Out[1329]: -1.11022302462516e-16
We can alternatively compute this as a binomial random variable:
In [1332]: n,p=4,1/6
In [1333]: sum([winom(n,i)*pw(p,i)*pw(1-p,n-i) for i in range(1,5)])
Out[1333]: 0.517746913580247
which is really the same computation. For instance
In [1334]: 4*pw(5,3)/pw(6,4)
Out[1334]: 0.38580246913580246
In [1335]: winom(n,1)*pw(p,1)*pw(1-p,n-1)
Out[1335]: 0.385802469135803
Notice that the binomial variable approximation is exact in this case. The reason is that rolling dice is comparable to “with replacement”. That is, the probability of each roll is always precisely $p$. Notice how this differs from problem (2.33) where the approximation was close but not precise because that problem modelled a “withOUT replacement” problem.
(2.42)
Probability that double $6$ doesn’t appear at least once: $\frac{35^n}{36^n}=\Bop\frac{35}{36}\Bcp^n$
In [1386]: n=25
In [1387]: 1-pw(35/36,n)
Out[1387]: 0.50553154623837826
Direct:
Total count: $6^{2n}$
Double six exactly once: $n\wts35^{n-1}$
To show this, let’s count the number of ways a double 6 appears only on the the first roll: $35^{n-1}$. The same goes for the second, third, …, $n^{th}$ rolls.
Double six exactly twice: $\binom{n}235^{n-2}$
Double six exactly three times: $\binom{n}335^{n-3}$
Double six exactly $n-2$ times: $\binom{n}{n-2}35^{n-(n-2)}=\binom{n}{n-2}35^2$
Double six exactly $n-1$ times: $\binom{n}{n-1}35^{n-(n-1)}=n35$
Double six exactly $n$ times: $\binom{n}n35^{n-n}=1$
In general, double six exactly $i$ times is $\binom{n}i35^{n-i}$
Hence
$$ \frac{\sum_{i=1}^{n}\binom{n}{i}35^{n-i}}{6^{2n}} $$
$$ =\sum_{i=1}^{n}\binom{n}{i}\frac{35^{n-i}}{6^{2n}}=\sum_{i=1}^{n}\binom{n}{i}\frac{35^n35^{-i}}{36^{n}} $$
$$ =\sum_{i=1}^{n}\binom{n}{i}\Bop\frac{35}{36}\Bcp^n\Bop\frac{1}{35}\Bcp^i $$
In [1414]: n=25
In [1415]: sum([winom(n,i)*pw(35/36,n)*pw(1/35,i) for i in range(1,n+1)])
Out[1415]: 0.505531546238378
In [1416]: n=24
In [1417]: sum([winom(n,i)*pw(35/36,n)*pw(1/35,i) for i in range(1,n+1)])
Out[1417]: 0.491403876130903
So it takes at least $25$ rolls to get a probability of $\frac12$ that a double $6$ appears at least once.
Notice that
$$ \Bop\frac{35}{36}\Bcp^n\Bop\frac{1}{35}\Bcp^i $$
$$ =\Bop\frac{35}{36}\Bcp^{i}\Bop\frac{35}{36}\Bcp^{-i}\Bop\frac{35}{36}\Bcp^n\Bop\frac{1}{35}\Bcp^i $$
$$ =\Bop\frac{35}{36}\Bcp^{n-i}\Bop\frac{35}{36}\frac{1}{35}\Bcp^i $$
$$ =\Bop\frac{35}{36}\Bcp^{n-i}\Bop\frac{1}{36}\Bcp^i $$
So this is just the binomial random variable.
(2.43.a)
Total count: $N!$
$A$ and $B$ next to each other count: $2\wts(N-1)\bop(N-2)!\bcp$
To show this, note that for $A,B$ together with $A$ on left, there are $N-1$ ways for this to occur: $A$ in first position, $A$ in second position, …, $A$ in $N-1$ position. In each case, the others can be seated in $(N-2)!$ ways.
Hence
$$ \frac{2(N-1)\bop(N-2)!\bcp}{N!}=\frac{2(N-1)}{N(N-1)}=\frac2{N} $$
(2.43.b)
- $\color{red}{1234}$
- $\color{red}{1243}$
- $\color{red}{1324}$
- $\color{red}{1342}$
- $\color{red}{1423}$
- $\color{red}{1432}$
- $2134$
- $2143$
- $2314$
- $2341$
- $2413$
- $2431$
- $3124$
- $3142$
- $3214$
- $3241$
- $3412$
- $3421$
- $4123$
- $4132$
- $4213$
- $4231$
- $4321$
- $4312$
These are the line permutations of $1$, $2$, $3$, and $4$. In red, we see the circle permutations. For each circle permutation, there are $4$ duplicate line permutations. For example, the first circle permutation $1234$ corresponds to $4$ duplicate line permutations: $1234$, $2341$, $3412$, and $4123$. We can see that each of these line permutations can be “curled” into a circle permutation where the relative order is $1234$.
Said another way, the list of line permutations consists of exactly $4$ duplicates of each circle permutation. Hence the count of line permutations is exactly $4$ times that of the count of the circle permutations.
Notice the reason for the duplicates: suppose we take the line permutation $1234$ and curl it into a circle so that the $1$ occupies seat $1$, the $2$ occupies seat $2$, the $3$ occupies seat $3$, and the $4$ occupies seat $4$. We can then clockwise rotate this arrangement by one seat. Now the $1$ occupies seat $2$, the $2$ occupies seat $3$, the $3$ occupies seat $4$, and the $4$ occupies seat $1$. Notice that the relative order in the circle is unchanged hence the circle permutation is unchanged. But if we were to uncurl the circle now into a line, this line permutation would be $4123$.
We can perform $4$ such rotations of $1234$ so that the circle permutation is unchanged and we get $4$ different line permutations. Similarly, we can perform $4$ such rotations of $1324$, $1423$, etc so that the circle permutation is unchanged while the lines permutations are different.
Succinctly, the count of line permutations is $4$ times the count of circle permutations. That is, the count of circle permutations is $\frac{4!}4=3!$.
Similarly, for a list of $n$ items, there are $n!$ line permutations and $\frac{n!}n=(n-1)!$ circle permutations.
Fun aside: $n!-(n-1)\bop(n-1)!\bcp=\frac{n!}n$:
$$ n!-(n-1)\bop(n-1)!\bcp-\frac{n!}n $$
$$ =n!-(n-1)\bop(n-1)!\bcp-(n-1)! $$
$$ =n!-(n-1)!\bop 1+(n-1) \bcp $$
$$ =n!-(n-1)!n $$
$$ =n!-n!=0 $$
Now back to this problem. We can assume that $A$ and $B$ are locked into specific chairs. The reason is that if we rotate everyone in the circle, the order is unchanged. Hence with $A$ and $B$ locked into position, the other $N-2$ persons can mixed into $(N-2)!$ permutations. Now we flip $A$ and $B$ and we disjointly get a second count of $(N-2)!$ permutations.
Hence the desired probability is
$$ \frac{2(N-2)!}{\frac{N!}N}=\frac{2(N-2)!}{(N-1)!}=\frac2{N-1} $$
(2.44.a)
With $A$ locked in slot $1$ and $B$ locked in slot $3$, there are exactly $3!$ permutations of $C, D$, and $E$. The same goes for $A\mapsto2, B\mapsto4$ and $A\mapsto3, B\mapsto5$. This is a total count of $3\wts3!$. Same count for $A$ and $B$ reversed.
$$ \frac{2\wts3\wts3!}{5!}=\frac{2\wts3}{5\wts4}=\frac{3}{10} $$
(2.44.b)
$$ \frac{2\wts2\wts3!}{5!}=\frac{2\wts2}{5\wts4}=\frac{1}{5} $$
(2.44.c)
$$ \frac{2\wts1\wts3!}{5!}=\frac{2}{5\wts4}=\frac{1}{10} $$
(2.45.a)
The probability that any one of the $n$ keys works is $\frac1n$ if we assume that each key is equally likely to work.
If we use the sample space $\Omega$ of all permutations of $n$ keys, then there are $n!$ outcomes in $\Omega$. Let $E_k$ denote the event that she opens the door on the $k^{th}$ try. Then $E_k$ contains permutations of $n$ keys such that the correct key is at the $k^{th}$ position. That is the correct key is fixed in a position. Hence $\wN{E_k}=(n-1)!$ and
$$ \pr{E_k}=\frac{\wN{E_k}}{\wN{\Omega}}=\frac{(n-1)!}{n!}=\frac1n $$
Another way to look at this: $\pr{E_1}=\frac{1}{n}$, $\pr{E_2}=\frac{n-1}{n}\frac{1}{n-1}=\frac1n$, and $\pr{E_3}=\frac{n-1}n\frac{n-2}{n-1}\frac1{n-2}=\frac1n$. Generally:
$$ \pr{E_k}=\frac{n-1}{n}\frac{n-2}{n-1}\frac{n-3}{n-2}\frac{n-4}{n-3}\wt\wt\wt\frac{1}{n-(k+1)}=\frac1n $$
(2.45.b)
Suppose $n=3$. In part (a), $\Omega=\set{(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)}$ where $(3,1,2)$ denotes the outcome that key $3$ was tried first, key $1$ was tried second, and key $2$ was tried third. In this part, let $\Omega_m$ be the sample space for $m$ tries. For $m=2$, we have
$$ \Omega_2=\set{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)} $$
Generally, since we can put any of $n$ keys into each of the $m$ slots, we have $\wN{\Omega_m}=n^m$.
Again let $E_k$ denote the event that she opens the door on the $k^{th}$ try. Suppose key $2$ is the valid key. Then $E_2=\set{(1,2),(3,2)}$. Similarly if key $1$ is the valid key, then $E_2=\set{(2,1),(3,1)}$, etc. Notice that the valid key cannot be in the first slot since $E_2$ denotes the event that she opens on the door in the $2^{nd}$ try.
Now suppose that $m=3$ and suppose key $1$ is the valid key. Then $\wN{\Omega_3}=3^3$ and
$$ E_2=\set{(2,1,1),(2,1,2),(2,1,3),(3,1,1),(3,1,2),(3,1,3)} $$
and $\wN{E_2}=(n-1)^{k-1}n^{m-k}=2^13^1=6$. Similarly, for $m=4$ and key $1$ is the valid key, we have
$$ E_3=\set{(2,2,1,1),(2,2,1,2),(2,2,1,3),(2,3,1,1),(2,3,1,2),(2,3,1,3)} $$
$$ \cup\set{(3,2,1,1),(3,2,1,2),(3,2,1,3),(3,3,1,1),(3,3,1,2),(3,3,1,3)} $$
and $\wN{E_3}=(n-1)^{k-1}n^{m-k}=2^23^1=12$.
In general, for $E_k$, we can put any of $n-1$ (invalid) keys into the first $k-1$ slots, one key (the valid key) into the $k^{th}$ slot, and any of $n$ keys into the last $m-k$ slots. Hence $\wN{E_k}=(n-1)^{k-1}n^{m-k}$ and
$$ \pr{E_k}=\frac{\wN{E_k}}{\wN{\Omega_m}}=\frac{(n-1)^{k-1}n^{m-k}}{n^m}=\frac{(n-1)^{k-1}}{n^k} $$
Alternatively, we can view this as a sequence of trials problem. The event $E_k$ that she will open the door on her $k^{th}$ attempt is precisely the sequence of $k$ (presumably) independent trials that she fails in her first $k−1$ attempts and succeeds on her $k^{th}$ attempt. Hence the probabilities $p_k=\pr{E_k}$ are
$$ p_1=\frac1n\dq p_2=\Bop1-\frac1n\Bcp\frac1n\dq p_3=\Bop1-\frac1n\Bcp^{2}\frac1n\dq $$
And
$$ p_k=\Bop1-\frac1n\Bcp^{k-1}\frac1n=\Bop\frac{n-1}n\Bcp^{k-1}\frac1n=\frac{(n-1)^{k-1}}{n^{k-1}}\frac1n=\frac{(n-1)^{k-1}}{n^{k}} $$
The last fraction matches the solutions manual and also makes intuitive sense: the probability of each failure is $\frac{n-1}n$, do that $k-1$ times, and finish with a success $\frac1n$.
Let’s check that the probabilities sum to $1$:
$$ \sum_{k=1}^{\infty}p_k=\frac1n\sum_{k=1}^{\infty}\Bop1-\frac1n\Bcp^{k-1}=\frac1n\sum_{j=0}^{\infty}\Bop1-\frac1n\Bcp^{j} $$
$$ =\frac1n\frac1{1-\bop1-\frac1n\bcp}=\frac1n\frac1{\frac1n}=1 $$
(2.46)
The probability that $2$ people in a room have the same birth month is $\frac1{12}$ since each month is equally likely.
With three people in the room, we have the disjoint and exhaustive events: $E_0, E_2, E_3$ where $E_i$ denotes the event that exactly $i$ people celebrate the same birth month.
$$ \wN{E_i}=\text{numb combs of persons w/same birth month }\times\text{ numb perms of diff birth months} $$
$$ \wN{E_0\cup E_2\cup E_3}=\binom3012\wts11\wts10+\binom3212\wts11+\binom3312 $$
In [109]: bmonth=lambda n:(sum([binom(n,i)*prod([12-j for j in range(0,n-i+(0 if i==0 else 1))]) for i in range(0,n+1) if i!=1]),pw(1
...: 2,n),1-(prod([12-j for j in range(0,n)]))/pw(12,n))
In [110]: bmonth(3)
Out[110]: (1728, 1728, 0.23611111111111116)
In [111]: bmonth(4)
Out[111]: (20340, 20736, 0.42708333333333337)
In [112]: bmonth(5)
Out[112]: (227712, 248832, 0.61805555555555558)
Notice there’s an error in my computation. The first two elements in the tuple should be equal.
(2.47)
Same situation as (2.46). Let $E_i$ denote the event that exactly $i$ people celebrate the same birth month. Then
$$ \wN{E_i}=\text{numb combs of persons w/same birth month }\times\text{ numb perms of diff birth months} $$
So that the desired probability is
$$ \frac{\binom{12}012!}{12^{12}} $$
In [122]: wf(12)/pw(12,12)
Out[122]: 5.3723217092478279e-05
(2.48)
Apparently this question means to ask, what is the probability that there are 4 months that each contain exactly 2 bdays and 4 months that each contain exactly 3 bdays.
$$ \frac{\binom{20}{2!2!2!2!3!3!3!3!}\binom{12}4\binom84}{12^{20}}=\frac{\binom{20}{(2!)^4(3!)^4}\binom{12}4\binom84}{12^{20}} $$
Let’s first investigate the use of $\binom{20}{2!2!2!2!3!3!3!3!}$. We will quote from p.9, the start of the Multinomial Coefficients section. A set of $20$ distinct items $-$ people $-$ is to be divided into $8$ distinct groups of respective sizes $2,2,2,2,3,3,3,3$, where $20=2+2+2+2+3+3+3+3$.
There are $\binom{20}2$ possible choices for the first group. For each choice of the first group, there are $\binom{18}2$ possible choices for the second group. For each choice of the first $2$ groups, there are $\binom{16}2$ possible choices for the third group. And so on.
After doing all the cancellations, the result is $\binom{20}{2!2!2!2!3!3!3!3!}$. So we have grouped $20$ distinct people into $8$ distinct groups. But now we want to assign each choice of $8$ groups to every possible “combination” of $8$ distinct months. Doing so will give us the count of ways that $20$ people can be grouped into $2,2,2,2,3,3,3,3$ fashion across the $12$ months of the year.
Hence we must choose $8$ distinct months for each choice of groupings. To count this, we use $\binom{12}4\binom84$. Notice that when we selected $8$ distinct groups, we selected $4$ that contain $2$ people each and another $4$ that contain $3$ people each. This should give us a hint that we don’t simply want $8$ combinations from $12$. Let’s keep this in mind while we examine a couple of subtleties in the way we assign a grouping to a selection of months.
First, we used combinations rather than permutations to choose the $4$ months that each contain $2$ bdays. That is, we used $\binom{12}4$ rather than $12\wts11\wts10\wts9$. The reason is that, in this case, Jan, Feb, Mar, Apr is a duplicate of Feb, Jan, Mar, Apr. The same goes for choosing the $4$ months that contain $3$ bdays: we used $\binom84$ rather than $8\wts7\wts6\wts5$. We’ll examine this momentarily.
Secondly, we used $\binom{12}4\binom84$ rather than $\binom{12}8$. The reason is that FOR EACH POSSIBLE combination of the $4$ months that contain $2$ bdays, we want to count ALL combinations of $4$ months from the remaining months. On top of that, we want to count the flips. By “flip”, we give an example: we wish to count separately the combos (Jan, Feb, Mar, Apr)-(May, Jun, Jul, Aug) and (May, Jun, Jul, Aug)-(Jan, Feb, Mar, Apr).
In the first case, (Jan, Feb, Mar, Apr)-(May, Jun, Jul, Aug), the months Jan, Feb, Mar, Apr each contain $2$ bdays and the months May, Jun, Jul, Aug each contain $3$ bdays. In the second case, (May, Jun, Jul, Aug)-(Jan, Feb, Mar, Apr), the months May, Jun, Jul, Aug each contain $2$ bdays and the months Jan, Feb, Mar, Apr each contain $3$ bdays.
Notice that $\binom{12}8$ will not count the flips but $\binom{12}4\binom84$ will do exactly that. To make this clear, let’s choose a smaller set.
Suppose we redefine a year to be the $5$ months Jan (J), Feb (F), Mar (M), Apr (A), and May (Z). And let’s also redefine the problem so that $2$ months each contain exactly $2$ people and another $2$ months each contain exactly $3$ people from a group of $10=2\wts2+2\wts3$ people. Hence we group the people as $\frac{10!}{2!2!3!3!}$. So we must determine the right way to count the $4$ months that contain $2$ or $3$ people.
The wrong way to count these $4$ months is $\binom54=\frac{5\wts4\wts3\wts2}{4!}=5$. Here are the combinations for this count:
- $\color{red}{JFMA}$
- $JFMZ$
- $JFAZ$
- $\color{blue}{JMAZ}$
- $FMAZ$
The months in the first and second slots each contain $2$ bdays and the months in the third and fourth slots each $3$ bdays.
Notice that we are missing many combinations that we want to see. For instance, we want to see the combinations $MAJF$ and $JMFA$. But these are permutations of $\color{red}{JFMA}$ which must be counted exactly once in the count $\binom54$.
Here’s another wrong way to count the desired $4$ months: $5\wts4\wts3\wts2=120$. In this case, we would count $\color{red}{JFMA}$ and $FJMA$ seperately. Similarly, we would count $\color{red}{JFMA}$ and $JFAM$ separately. But counting these permutations separately results in a double count. Let’s examine this.
When we first group people, we get every combination. Let’s take an example. Suppose the people are named $A, B, C, D, E, F, G, H, I, J$. Once such grouping is $(A, B), (C, D), (E, F, G), (H, I, J)$. Another such grouping is $(C, D), (A, B), (E, F, G), (H, I, J)$. When we assign these groupings to $\color{red}{JFMA}$ and $FJMA$, we see the problem:
- $(A, B), (C, D), (E, F, G), (H, I, J)$ $\mapsto$ $\color{red}{JFMA}$
- $(A, B), (C, D), (E, F, G), (H, I, J)$ $\mapsto$ $FJMA$
- $(C, D), (A, B), (E, F, G), (H, I, J)$ $\mapsto$ $\color{red}{JFMA}$
- $(C, D), (A, B), (E, F, G), (H, I, J)$ $\mapsto$ $FJMA$
Notice that assignments (1) and (4) are identical. The same groups of people are assigned to the same months. Similarly, assignments (2) and (3) are identical. This is why $FJMA$ is considered a duplicate and hence why the count $5\wts4\wts3\wts2=120$ is wrong.
Here’s the correct count: $\binom52\binom32=\frac{5\wts4}2\frac{3\wts2}2=10\wts3=30$. And here are the combinations:
- $\color{red}{JF-MA}$
- $JF-MZ$
- $JF-AZ$
- $\color{red}{JM-FA}$
- $JM-FZ$
- $\color{blue}{JM-AZ}$
- $\color{red}{JA-FM}$
- $JA-FZ$
- $\color{blue}{JA-MZ}$
- $JZ-FM$
- $JZ-FA$
- $\color{blue}{JZ-MA}$
- $\color{red}{FM-JA}$
- $FM-JZ$
- $FM-AZ$
- $\color{red}{FA-JM}$
- $FA-JZ$
- $FA-MZ$
- $FZ-JM$
- $FZ-JA$
- $FZ-MA$
- $\color{red}{MA-JF}$
- $\color{blue}{MA-JZ}$
- $MA-FZ$
- $MZ-JF$
- $\color{blue}{MZ-JA}$
- $MZ-FA$
- $AZ-JF$
- $\color{blue}{AZ-JM}$
- $AZ-FM$
We have highlighted in $\color{red}{RED}$ the permutations of $\color{red}{JF-MA}$. And we have highlighted in $\color{blue}{BLUE}$ the permutations of $\color{blue}{JM-AZ}$.
Notice that we now see the desired permutations $\color{red}{MA-JF}$ and $\color{red}{JM-FA}$ that were missing in the first wrong count. The reason is that the binomial coefficient $\binom54$ is now split into $\binom52\binom32$. Whereas $\color{red}{JFMA}$ and its flip $MAJF$ could not be counted separately in $\binom54$, the count $\binom52\binom32$ does count them separately.
Similarly, the count $\binom54$ could not accomodate both $\color{red}{JFMA}$ and $JMFA$ because these are permutations of each other. But the count $\binom52\binom32$ looks for ALL $2$ element combinations from the given $5$ $-$ including both $JF$ and $JM$ $-$ and then looks for ALL $2$ element combinations from the remaining $3$ $-$ including both $MA$ and $FA$, when they’re remaining.
Also notice that we now avoid the unwanted permutations $FJ-MA$ and $JF-AM$ mentioned in the second wrong count. The reason is that $\binom52$ ensures that, for a given $X$ and $Y$, the $JF-XY$ and $FJ-XY$ combinations are counted once, not twice. Similarly the $\binom32$ ensures that, for a given $X$ and $Y$, the $XY-MA$ and $XY-AM$ combinations are counted once.
In short, when we choose the $8$ months to which we apply the chosen $4\times4$ groups of birthdays, we must choose every combination of $4\times4$ months.
(2.49)
For each group to have the same number of men, each group must have $3$ men. Since each group is of size $6=\frac{12}2$, then each group must also have $3$ women.
By choosing the $3$ men and $3$ women for one group, we automatically decide the men and women for the other group. That is, for each choice of $3$ men and $3$ women for one group, there is exactly $1$ selection of men and women for the other group. Hence
$$ \frac{\binom63\binom63\wts1}{\binom{12}6}=\frac{\binom63\binom63}{\binom{12}6} $$
(2.50)
Choose $5$ spades from $13$, choose $8$ cards from $39=52-13$ non-spades to complete my hand, choose $13$ cards from the remaining $31=39-8$ non-spades for the $1^{st}$ guy on the other team, choose the last $8$ spades for my partner, choose $5$ cards from the remaining $18=31-13$ non-spades, and give the remaining $13$ cards to the last guy:
$$ \frac{\binom{13}5\binom{39}8\binom{31}{13}\binom88\binom{18}5\binom{13}{13}}{\binom{52}{13,13,13,13}} $$
$$ =\frac{\binom{13}5\binom{39}8\binom{31}{13}\binom{18}5}{\binom{52}{13,13,13,13}} $$
Another way to compute this is to note that once I choose my $5$ spades, the $8$ spades to my partner are determined, and the remaining $39$ cards are all non-spades that can be chosen in groups. Hence
$$ \frac{\binom{13}5\binom{39}{8,13,5,13}}{\binom{52}{13,13,13,13}} $$
But of course this is really the same computation:
$$ \binom{39}{8,13,5,13}=\frac{39!}{8!13!5!13!} $$
$$ =\frac{39\dwt32\wts31\dwt19\wts18\dwt14\wts13!}{8!13!5!13!} $$
$$ =\frac{39\dwt32}{8!}\frac{31\dwt19}{13!}\frac{18\dwt14}{5!}\frac{13!}{13!} $$
$$ =\binom{39}8\binom{31}{13}\binom{18}5\binom{13}{13} $$
$$ =\binom{39}8\binom{31}{13}\binom{18}5 $$
I don’t agree with the solution manual. There is amguity about the deal which I feel should mean that every player gets dealt a hand. It doesn’t appear to me that the given solution accounts for this.
(2.51)
$$ \frac{\binom{n}m(N-1)^{(n-m)}}{N^n} $$
(2.52.a)
First we choose $8$ pairs and then we choose $1$ of the $2$ shoes from each of those $8$ pairs:
Combinations
$$ \frac{\binom{10}82^{8}}{\binom{20}8} $$
or permutations
$$ \frac{10\wts9\wts8\wts7\wts6\wts5\wts4\wts3\wts2^{8}}{20\wts19\wts18\wts17\wts16\wts15\wts14\wts13} $$
In [174]: winom(10,8)*pw(2,8)/winom(20,8)
Out[174]: 0.0914503453203144
In [175]: 10*9*8*7*6*5*4*3*pw(2,8)/(20*19*18*17*16*15*14*13)
Out[175]: 0.091450345320314361
Alternatively we can select from $20$, remove the other shoe (the other in the pair of the first selected shoe), select from $18$, remove the other, select from $16$, etc:
$$ \frac{20\wts18\wts16\wts14\wts12\wts10\wts8\wts6}{20\wts19\wts18\wts17\wts16\wts15\wts14\wts13} $$
In [176]: 12*10*8*6/(19*17*15*13)
Out[176]: 0.09145034532031436
(2.52.b)
$$ \frac{\binom{10}{1}\binom{9}62^{6}}{\binom{20}8} $$
In [189]: binom(10,1)*binom(9,6)*pw(2,6)/winom(20,8)
Out[189]: 0.426768278161467
Note that the solutions manual is wrong. Notice the probabilities sum to one this way:
In [188]: 12*10*8*6/(19*17*15*13)
Out[188]: 0.09145034532031436
In [189]: binom(10,1)*binom(9,6)*pw(2,6)/winom(20,8)
Out[189]: 0.426768278161467
In [190]: binom(10,2)*binom(8,4)*pw(2,4)/winom(20,8)
Out[190]: 0.400095260776375
In [191]: binom(10,3)*binom(7,2)*pw(2,2)/winom(20,8)
Out[191]: 0.0800190521552751
In [192]: binom(10,4)*binom(6,0)*pw(2,0)/winom(20,8)
Out[192]: 0.00166706358656823
In [193]: 12*10*8*6/(19*17*15*13)+binom(10,1)*binom(9,6)*pw(2,6)/winom(20,8)+binom(10,2)*binom(8,4)*pw(2,4)/winom(20,8)+binom(10,3)*b
...: inom(7,2)*pw(2,2)/winom(20,8)+binom(10,4)*binom(6,0)*pw(2,0)/winom(20,8)
Out[193]: 1.00000000000000
(2.53)
Let $E_i$ denote the event that couple $i$ sits together (the other couples may or may not sit together). Then, in isolation, there are two ways that couple $i$ can sit together. For each of these permutations, we have $7$ entities, $1$ couple and $6$ individuals, for which we must count permutations. That’s $7!$. Hence
$$ \wN{E_i}=2\wts7! $$
$E_iE_j$: in isolation, there are $2$ ways that couple $i$ can sit together. For each of these, there are $2$ ways that couple $j$ can sit together. So that’s $2^2$ so far. For each of these permutations, we have $6$ entities, $2$ couples and $4$ individuals, for which we must count permutations. That’s $6!$. Hence
$$ \wN{E_iE_j}=2^26! $$
There are $2^3$ permutations of $3$ couples sitting together, each in isolation. For each of these permutations, we have $5$ entities, $3$ couples and $2$ individuals, for which we must count permutations. That’s $5!$. Hence
$$ \wN{E_iE_jE_k}=2^35! $$
Similarly
$$ \wN{E_1E_2E_3E_4}=2^44! $$
The inclusion-exclusion identity gives us
$$ \prB{\bigcup_{i=1}^{4}E_i}=\sum_{i=1}^4\pr{E_i}-\sum_{i<j}\pr{E_iE_j}+\sum_{i<j<k}\pr{E_iE_jE_k}-\sum_{i<j<k<m}\pr{E_iE_jE_kE_m} $$
The first sum has $\binom41=4$ terms, the second sum has $\binom42=6$ terms, the third sum has $\binom43=4$ terms, and the third sum has $\binom44=1$ terms. Since each probability $\pr{E_i}, \pr{E_iE_j},…$ is constant, we have
$$ \prB{\bigcup_{i=1}^{4}E_i}=4\frac{2\wts7!}{8!}-6\frac{2^26!}{8!}+4\frac{2^35!}{8!}-\frac{2^44!}{8!} $$
$$ =4\wts\frac28-6\wts\frac4{8\wts7}+4\wts\frac8{8\wts7\wts6}-\frac{16}{8\wts7\wts6\wts5} $$
$$ =1-\frac6{2\wts7}+\frac4{7\wts6}-\frac{2}{7\wts6\wts5} $$
$$ =1-\frac3{7}+\frac2{7\wts3}-\frac{1}{7\wts3\wts5} $$
$$ =1-\frac{3\wts15}{7\wts3\wts5}+\frac{2\wts5}{7\wts3\wts5}-\frac{1}{7\wts3\wts5} $$
$$ =1+\frac{10-45-1}{7\wts3\wts5} $$
$$ =1-\frac{36}{7\wts3\wts5} $$
$$ =1-\frac{12}{7\wts5} $$
But $\bigcup_{i=1}^{4}E_i$ is just the event that at least $1$ couple sat together. This event is exclusive and exhaustive with the event that no couples sat together. Hence
$$ \prt{no couples sit together}=1-\Bop1-\frac{12}{35}\Bcp=\frac{12}{35} $$