(4.1)
$$ \pr{X=4}=\frac{\binom42}{\binom{14}2}=\frac6{91}\dq\pr{X=-2}=\frac{\binom82}{\binom{14}2}=\frac{28}{91} $$
$$ \pr{X=0}=\frac{\binom22}{\binom{14}2}=\frac1{91}\dq\pr{X=2}=\frac{\binom41\binom21}{\binom{14}2}=\frac{8}{91} $$
$$ \pr{X=1}=\frac{\binom81\binom41}{\binom{14}2}=\frac{32}{91}\dq\pr{X=-1}=\frac{\binom81\binom21}{\binom{14}2}=\frac{16}{91} $$
Probability of drawing each permutation
- $ww: \frac8{14}\frac7{13}=\frac{4\wts7}{91}\quad X=-2$
- $bb: \frac4{14}\frac3{13}=\frac{6}{91}\quad X=4$
- $oo: \frac2{14}\frac1{13}=\frac{1}{91}\quad X=0$
- $wb: \frac8{14}\frac4{13}=\frac{16}{91}\quad X=1$
- $bw: \frac4{14}\frac8{13}=\frac{16}{91}\quad X=1$
- $wo: \frac8{14}\frac2{13}=\frac8{91}\quad X=-1$
- $ow: \frac2{14}\frac8{13}=\frac8{91}\quad X=-1$
- $bo: \frac4{14}\frac2{13}=\frac{4}{91}\quad X=2$
- $ob: \frac2{14}\frac4{13}=\frac{4}{91}\quad X=2$
(4.2)
$$ \pr{X=1}=\pr{X_1=1,X_2=1}=\pr{X_1=1}\pr{X_2=1}=\frac16\frac16=\frac1{36} $$
$$ \pr{X=2}=\pr{X_1=1,X_2=2}+\pr{X_1=2,X_2=1}=\pr{X_1=1}\pr{X_2=2}+\pr{X_1=2}\pr{X_2=1}=\frac1{36}+\frac1{36}=\frac2{36} $$
$$ \pr{X=3}=\pr{X_1=1,X_2=3}+\pr{X_1=3,X_2=1}=\pr{X_1=1}\pr{X_2=3}+\pr{X_1=3}\pr{X_2=1}=\frac1{36}+\frac1{36}=\frac2{36} $$
$$ \pr{X=4}=\pr{X_1=1,X_2=4}+\pr{X_1=4,X_2=1}+\pr{X_1=2,X_2=2} $$
$$ =\pr{X_1=1}\pr{X_2=4}+\pr{X_1=4}\pr{X_2=1}+\pr{X_1=2}\pr{X_2=2}=\frac1{36}+\frac1{36}+\frac1{36}=\frac3{36} $$
etc
(4.3)
$$ \pr{X=3}=\pr{X_1=1,X_2=1,X_3=1}=\pr{X_1=1}\pr{X_2=1}\pr{X_3=1}=\frac16\frac16\frac16=\frac1{216} $$
$$ \pr{X=4}=\pr{X_1=1,X_2=1,X_3=2}+\pr{X_1=1,X_2=2,X_3=1}+\pr{X_1=2,X_2=1,X_3=1}=\frac3{216} $$
etc
(4.4)
$$ \pr{X=1}=\frac{5}{10}\frac{9!}{9!}=\frac12 $$
$$ \pr{X=2}=\frac5{10}\frac59\frac{8!}{8!}\approx0.2777 $$
$$ \pr{X=3}=\frac5{10}\frac49\frac58\approx0.1388 $$
$$ \pr{X=4}=\frac5{10}\frac49\frac38\frac57\approx0.0595 $$
(4.5)
If $n$ is even, $X$ will be even: $n,n-2,n-4,…2,0,-2,…,2-n,-n$
If $n$ is odd, $X$ will be odd: $n,n-2,n-4,…2,0,-2,…,2-n,-n$
(4.6)
- $3h,0t\quad X=3\quad \pr{X=3}=\binom33\bop\frac12\bcp^3\bop\frac12\bcp^0=\frac18$
- $2h,1t\quad X=1\quad \pr{X=1}=\binom32\bop\frac12\bcp^2\bop\frac12\bcp^1=\frac38$
- $1h,2t\quad X=-1\quad \pr{X=-1}=\binom31\bop\frac12\bcp^1\bop\frac12\bcp^2=\frac38$
- $0h,3t\quad X=-3\quad \pr{X=-3}=\binom30\bop\frac12\bcp^0\bop\frac12\bcp^3=\frac18$
(4.7)
- $1,2,3,4,5,6$
- $1,2,3,4,5,6$
- $2,3,4,5,6,7,8,9,10,11,12$
- $-5,-4,-3,-2,-1,0,1,2,3,4,5$
(4.8)
a.
$p(1)=\frac16\frac16=\frac1{36}$
$p(2)=\frac3{36}=\frac1{12}$
$p(3)=\frac5{36}$
$p(4)=\frac7{36}$
etc
(4.9)
There are $20$ options for each of the three numbers that we observe. So $\norm{\Omega} = 20^3$. Let’s count the number of outcomes whose largest number is $i$. There are three cases to consider.
- Only one of the three numbers is $i$, and the other two are less than $i$: we have $3$ ways to choose which number is $i$ (that is, the first, the second, or the third number). For the remaining numbers, we have $(i − 1)^2$ choices. So there are $3(i − 1)^2$ such cases.
- Two of the three numbers are $i$, and the other is less than $i$: we have $3$ ways to choose which number is less than $i$ and then we have $i − 1$ options for the value of this number. So there are $3(i − 1)$ such cases.
- All three numbers are equal to $i$. There is one such case.
Hence $\norm{\set{X = i}} = 3(i − 1)^2+3(i − 1)+1=3i(i − 1)+1$ and so
$$ \pmfa{i}{X}=\frac{3i(i-1)+1}{20^3} $$
$$ \pr{X\geq17}=\pmf{17}+\pmf{18}+\pmf{19}+\pmf{20} $$
In [1885]: pic=lambda i:(3*i*(i-1)+1)/pw(20,3)
In [1886]: picl=[pic(i) for i in range(17,21)]
In [1887]: picl
Out[1887]: [0.10212499999999999, 0.114875, 0.12837499999999999, 0.142625]
In [1888]: sum(picl)
Out[1888]: 0.48799999999999999
(4.10)
The probability that we win something is
$$ \pr{W}=\pr{\cup_{i=1}^3X_i}=\sum_{i=1}^3\pr{X=i}=\frac{55}{165}=\frac13 $$
Since $\set{X=i}\subset W$ for $i=1,2,3$, we have
$$ \cp{X=1}W=\frac{\pr{W\cap\set{X=1}}}{\pr{W}}=\frac{\pr{X=1}}{\pr{W}}=\frac{\frac{39}{165}}{\frac13}\approx0.7091 $$
$$ \cp{X=2}W=\frac{\frac{15}{165}}{\frac13}\approx0.2727 $$
$$ \cp{X=3}W=\frac{\frac{1}{165}}{\frac13}\approx0.01818 $$
(4.13)
$$ \pr{X=0}=0.7\wts0.4=0.28 $$
$$ \pr{X=500}=0.3\wts0.5\wts0.4+0.6\wts0.5\wts0.7=0.27 $$
$$ \pr{X=1000}=0.3\wts0.5\wts0.4+0.6\wts0.5\wts0.7+0.3\wts0.5\wts0.6\wts0.5=0.315 $$
$$ \pr{X=1500}=0.3\wts0.5\wts0.6\wts0.5+0.6\wts0.5\wts0.3\wts0.5=0.27=0.09 $$
$$ \pr{X=2000}=0.3\wts0.5\wts0.6\wts0.5=0.045 $$
(4.14)
$$ \pr{X=0}=\prt{of players 1 and 2: player 2 has the larger number}=\frac12 $$
Now $\set{X=1}$ implies that player $1$ has a higher number that player $2$ but that player $3$ has a higher number than all $3$ of them. Let’s look at the probabilities of such a distribution to players $1,2,$ and $3$. Of these three, there is a $\frac13$ chance of player $3$ having the largest number. And of players $1$ and $2$, there is a $\frac12$ chance of player $1$ having the larger number. Hence
$$ \pr{X=1}=\prt{of players 1, 2, 3: player 3 has largest, then 1, then 2}=\frac13\frac12=\frac16 $$
Similarly $\set{X=2}$ means that player $4$ has the largest number of players $1,2,3,$ and $4$. This event occurs with probability $\frac14$. Then player $1$ has the largest number of players $1,2,$ and $3$. This event occurs with probability $\frac13$.
$$ \pr{X=2}=\prt{of 1, 2, 3, 4: 4 has largest, 1 has next largest, then any}=\frac14\frac13=\frac1{12} $$
$$ \pr{X=3}=\prt{of 1, 2, 3, 4, 5: 5 has largest, 1 has next largest, then any}=\frac15\frac14=\frac1{20} $$
$$ \pr{X=4}=\prt{of 1, 2, 3, 4, 5: 1 has largest, then any}=\frac15 $$
Alternative computation:
Let $A_i$ denote the event that player $1$ wins atleast $i$ times. Then
$$ \pr{A_0}=1 \dq\pr{A_1}=\frac12 \dq\pr{A_2}=\frac13 \dq\pr{A_3}=\frac14 \dq\pr{A_4}=\frac15 $$
Notice that $A_0\supset A_1\supset A_2\supset A_3\supset A_4$. For instance, say event $A_1$ occurs. This means that player $1$ got at least $1$ win, which means he got at least $0$ wins, which means event $A_0$ occurred.
Similarly, say event $A_2$ occurs. This means that player $1$ got at least $2$ wins, which means he got at least $1$ win, which means event $A_1$ occurred.
Now let $X_i$ denote the event that player $1$ wins exactly $i$ times. Then $X_i=A_iA_{i+1}^c=A_i-A_{i+1}$. For instance, if he won exactly $0$ times, then he must have won at least $0$ times but he must not have won at least $1$ time.
Similarly, say event $X_1$ occurred. Then he won exactly $1$ time, which means he won at least once but he did not win at least twice, which means event $A_1$ occurred but event $A_2$ did not occur. The reverse argument also works: suppose the event $A_1A_2^c$ occurred. Then he won at least once but did not win at least twice. This means he won exactly once, which means event $X_1$ occurred.
Since $A_i\supset A_{i+1}$, then $\pr{A_iA_{i+1}^c}=\pr{A_i-A_{i+1}}=\pr{A_i}-\pr{A_{i+1}}$ and we have
$$ \pr{X_0}=\pr{A_0A_1^c}=\pr{A_0}-\pr{A_1}=1-\frac12=\frac12 $$
$$ \pr{X_1}=\pr{A_1A_2^c}=\pr{A_1}-\pr{A_2}=\frac12-\frac13=\frac16 $$
$$ \pr{X_2}=\pr{A_2}-\pr{A_3}=\frac13-\frac14=\frac1{12} $$
$$ \pr{X_3}=\frac14-\frac15=\frac1{20}\dq\pr{X_4}=\pr{A_4}=\frac15 $$
(4.15)
$$ \pr{X=1}=\frac{11}{66}=\frac16 $$
Team $1$ has the worst record. Team $2$ has the second worst record,…, team $i$ has the $i^{th}$ worst record. Conditioning $\set{X=2}$ on \(\set{\text{team $i$ chosen first}}\) and noting that \(\cpttwo{X=2}{team $1$ chosen first}=0\), we see that
$$ \pr{X=2}=\sum_{i=1}^{11}\cpttwo{X=2}{team $i$ chosen first}\prt{team $i$ chosen first} $$
$$ =\sum_{i=2}^{11}\cpttwo{X=2}{team $i$ chosen first}\prt{team $i$ chosen first} $$
$$ =\sum_{i=2}^{11}\frac{11}{66-(12-i)}\frac{12-i}{66} $$
$$ =\frac16\sum_{i=2}^{11}\frac{12-i}{54+i} $$
In [170]: wst2=[(1/6)*(12-i)/(54+i) for i in range(2,12)]
In [173]: sum(wst2)
Out[173]: 0.15562971214059629
Similarly
$$ \pr{X=3}=\sum_{i=2}^{11}\cpttwo{X=3}{team $i$ chosen first}\prt{team $i$ chosen first} $$
$$ =\sum_{i=2}^{11}\cpttwo{X=3}{team $i$ chosen first}\frac{12-i}{66} $$
$$ =\sum_{i=2}^{11}\sum_{j=2}^{11}\cpttwo{X=3}{$j$ chosen second & $i$ chosen first}\cpt{$j$ chosen second}{team $i$ chosen first}\frac{12-i}{66} $$
$$ =\sum_{i=2}^{11}\sum_{j=2,j\neq i}^{11}\cpttwo{X=3}{$j$ chosen second & $i$ chosen first}\cpt{$j$ chosen second}{team $i$ chosen first}\frac{12-i}{66} $$
$$ =\sum_{i=2}^{11}\sum_{j=2,j\neq i}^{11}\frac{11}{66-(12-i)-(12-j)}\frac{12-j}{66-(12-i)}\frac{12-i}{66} $$
$$ =\sum_{i=2}^{11}\sum_{j=2,j\neq i}^{11}\frac{11}{42+i+j}\frac{12-j}{54+i}\frac{12-i}{66} $$
In [49]: wst=[(11/(42+i+j))*((12-j)/(54+i))*((12-i)/66) for i in range(2,12) for j in range(2,12) if j!=i]
In [50]: sum(wst)
Out[50]: 0.14347569986326086
Since the first team can acquire only the first, second, third, or fourth draft picks (and no higher draft picks), then we have
$$ \pr{X=4}=1-\bop \pr{X=1}+\pr{X=2}+\pr{X=3} \bcp=0.5342279 $$
(4.16)
$$ \pr{Y_1=k}=\frac{12-k}{66} $$
$$ \pr{Y_2=k}=\sum_{i=1}^{11}\cp{\settx{team k chosen second}}{\text{team $i$ chosen first}}\pr{\text{team $i$ chosen first}} $$
$$ =\sum_{i=1,i\neq k}^{11}\cp{\settx{team k chosen second}}{\text{team $i$ chosen first}}\pr{\text{team $i$ chosen first}} $$
$$ =\sum_{i=1,i\neq k}^{11}\frac{12-k}{66-(12-i)}\frac{12-i}{66} $$
$$ =\sum_{i=1,i\neq k}^{11}\frac{12-k}{54+i}\frac{12-i}{66} $$
Similarly
$$ \pr{Y_3=k}=\sum_{i=1,i\neq k}^{11}\sum_{j=1,j\neq i,k}^{11}\frac{12-k}{42+i+j}\frac{12-j}{54+i}\frac{12-i}{66} $$
(4.17)
$$ \pr{X\leq1}=F(1)=\frac12 $$
$$ \pr{X<1}=\lim_{b\goesto1^-}F(b)=\lim_{b\goesto1^-}\frac{b}4=\frac14 $$
$$ \pr{X=1}=\pr{X\leq1}-\pr{X<1}=\frac12-\frac14=\frac14 $$
$$ \pr{X=2}=\pr{X\leq2}-\pr{X<2}=F(2)-F(2^-)=\frac{11}{12}-\frac34=\frac16 $$
$$ \pr{X=3}=F(3)-F(3^-)=1-\frac{11}{12}=\frac1{12} $$
For part (b), we note that
$$ \Bset{X<\frac32}=\Bset{X\leq\frac12}\cup\Bset{\frac12<X<\frac32} $$
and that the two sets on the right side are mutually exclusive. Hence
$$ \prB{X<\frac32}=\prB{X\leq\frac12}+\prB{\frac12<X<\frac32} $$
Thus
$$ \prB{\frac12<X<\frac32}=\prB{X<\frac32}-\prB{X\leq\frac12}=F\Bop\frac32^-\Bcp-F\Bop\frac12\Bcp $$
$$ =\frac12+\frac{\frac32-1}4-\frac{\frac12}4 $$
$$ =\frac12+\frac{\frac12}4-\frac{\frac12}4=\frac12 $$
(4.18)
In general, we have
$$ \pr{X=i}=\binom4i\Bop\frac12\Bcp^i\Bop\frac12\Bcp^{4-i}=\binom4i\frac1{2^4}=\binom4i\frac1{16} $$
So
$$ \pr{X=0}=\binom40\frac1{16}=\frac1{16} \dq\pr{X=1}=\binom41\frac1{16}=\frac14 $$
- $hhtt$
- $htht$
- $htth$
- $thht$
- $thth$
- $tthh$
$$ \pr{X=2}=\binom42\frac1{16}=\frac38 \dq\pr{X=3}=\binom43\frac1{16}=\frac14 \dq\pr{X=4}=\frac1{16} $$
Check:
$$ \pr{X=0}+\pr{X=1}+\pr{X=2}+\pr{X=3}+\pr{X=4} $$
$$ =\frac1{16}+\frac1{16}+\frac14+\frac14+\frac38=\frac2{16}+\frac24+\frac38=\frac18+\frac48+\frac38=1 $$
Let $Y=X-2$. Then
$$ \pr{Y=-2}=\pr{Y=2}=\frac1{16} \dq\pr{Y=-1}=\pr{Y=1}=\frac14 \dq\pr{Y=0}=\frac38 $$
(4.19)
$$ \pmfa{0}{X}=\frac12 \dq\pmf{1}=\frac35-\frac12=\frac1{10} \dq\pmf{2}=\frac45-\frac32=\frac15 $$
$$ \pmf{3}=\frac1{10} \dq\pmf{3.5}=\frac1{10} $$
(4.20)
$$ \pr{X>0}=\frac{18}{38}+\frac{20}{38}\frac{18}{38}\frac{18}{38}\approx0.5917772270 $$
We don’t yet know if this is a winning strategy because we have not taken into account how much we lose when we lose. Nor have we accounted for how much we win when we win. That is, we haven’t computed the expected value, which really determines whether a strategy is winning:
$$ \evw{X}=\$1\wts\Prn{\frac{18}{38}+\frac{20}{38}\frac{18}{38}\frac{18}{38}}-\$3\wts\Prn{\frac{20}{38}\frac{20}{38}\frac{20}{38}}-\$1\wts\Prn{\frac{20}{38}\frac{18}{38}\frac{20}{38}+\frac{20}{38}\frac{20}{38}\frac{18}{38}} $$
In [181]: 1*((18/38)+(20/38)*(18/38)*(18/38))-3*((20/38)*(20/38)*(20/38))-1*((20/38)*(18/38)*(20/38)+(20/38)*(20/3
...: 8)*(18/38))
Out[181]: -0.10803324099722977
Let’s checksum the probabilities:
In [182]: 1*((18/38)+(20/38)*(18/38)*(18/38))+((20/38)*(20/38)*(20/38))+((20/38)*(18/38)*(20/38)+(20/38)*(20/38)*(
...: 18/38))
Out[182]: 1.0
Since the expected value is negative, then this is not a winning strategy.
(4.21)
$E[X]$ should be bigger than $E[Y]$ because the selected bus driver is equally likely to be from any of the 4 buses, whereas the selected student is more likely to have come from a bus carrying a large number of students:
$$ E[Y]=\frac14\wts(40+33+25+50)=37.0 $$
$$ E[X]=\frac{40^2}{148}+\frac{33^2}{148}+\frac{25^2}{148}+\frac{50^2}{148} $$
In [185]: (pw(40,2)+pw(33,2)+pw(25,2)+pw(50,2))/148
Out[185]: 39.283783783783782
(4.22.a)
$$ p(2)=p^2+(1-p)^2=p^2+1-2p+p^2=2p^2-2p+1 $$
- $ABA$
- $BAA$
- $\cancel{AAB}$
$$ p(3)=2p^2(1-p)+2p(1-p)^2=2p(1-p)\bop p+(1-p) \bcp=2p(1-p) $$
Check sum to 1:
$$ p(2)+p(3)=2p^2-2p+1+2p(1-p) $$
$$ =2p^2-2p+1+2p-2p^2 $$
$$ =1 $$
Our expected value is
$$ E[N]=2\wt p(2)+3\wt p(3) $$
$$ =2\wt(2p^2-2p+1)+3\wt(2p-2p^2) $$
$$ =4p^2-4p+2+6p-6p^2 $$
$$ =-2p^2+2p+2 $$
$$ =2(p-p^2+1) $$
Finding the max
$$ 0=\wderiv{E[N]}{p}=-4p+2 $$
$$ 4p=2 $$
$$ p=\frac12 $$
So $p=\frac12$ is a stationary point. The second derivative test will tell us whether $p=\frac12$ is a max or min:
$$ \wderivn{E[N]}{p}{2}=-4<0 $$
so that $p=\frac12$ is a maximum of $E[N]$.
(4.22.b)
$$ p(3)=p^3+(1-p)^3 $$
$$ =p^3+(1-2p+p^2)(1-p) $$
$$ =p^3+1-2p+p^2-p+2p^2-p^3 $$
$$ =1-2p+p^2-p+2p^2 $$
$$ =3p^2-3p+1 $$
- $AABA$
- $ABAA$
- $BAAA$
- $\cancel{AAAB}$
$$ p(4)=3p^3(1-p)+3p(1-p)^3 $$
$$ =3p^3-3p^4+3p(1-2p+p^2-p+2p^2-p^3) $$
$$ =3p^3-3p^4+3p(1-3p+3p^2-p^3) $$
$$ =3p^3-3p^4+3p-9p^2+9p^3-3p^4 $$
$$ =-6p^4+12p^3-9p^2+3p $$
- $BBAAA$
- $BABAA$
- $BAABA$
- $ABBAA$
- $ABABA$
- $AABBA$
- $\cancel{BAAAB}$
- $\cancel{ABAAB}$
- $\cancel{AABAB}$
- $\cancel{AAABB}$
$$ p(5)=6\bocb p^3(1-p)^2+p^2(1-p)^3 \bccb $$
$$ =6\bocb p^3(1-2p+p^2)+p^2(1-2p+p^2-p+2p^2-p^3) \bccb $$
$$ =6\bocb p^3-2p^4+p^5+p^2(1-3p+3p^2-p^3) \bccb $$
$$ =6\bocb p^3-2p^4+p^5+p^2-3p^3+3p^4-p^5 \bccb $$
$$ =6\bocb p^3-2p^4+p^2-3p^3+3p^4 \bccb $$
$$ =6(p^4-2p^3+p^2) $$
Check sum to 1:
$$ p(3)+p(4)+p(5) $$
$$ =3p^2-3p+1-6p^4+12p^3-9p^2+3p+6p^4-12p^3+6p^2 $$
$$ =3p^2-3p+1+12p^3-9p^2+3p-12p^3+6p^2 $$
$$ =3p^2-3p+1-9p^2+3p+6p^2 $$
$$ =3p^2+1-9p^2+6p^2 $$
$$ =1 $$
The expected value of the number of games is
$$ E[N]=3p(3)+4p(4)+5p(5) $$
$$ =3\bop3p^2-3p+1\bcp+4\bop-6p^4+12p^3-9p^2+3p\bcp+5\bop6p^4-12p^3+6p^2\bcp $$
$$ =9p^2-9p+3-24p^4+48p^3-36p^2+12p+30p^4-60p^3+30p^2 $$
$$ =30p^4-24p^4+48p^3-60p^3+9p^2-36p^2+30p^2-9p+12p+3 $$
$$ =6p^4-12p^3+3p^2+3p+3 $$
We differentiate to find stationary points:
$$ \wderiv{E[N]}{p}=24p^3-36p^2+6p+3 $$
In [1896]: np.roots([24,-36,6,3])
Out[1896]: array([ 1.20710678, 0.5 , -0.20710678])
Check the second derivative:
$$ \wderivn{E[N]}{p}{2}\evall{\frac12}=(72p^2-72p+6)\evall{\frac12}=72\Prn{\frac14-\frac12}+6<0 $$
Hence $p=\frac12$ is a max of $\evw{N}(p)$ on $[0,1]$.
(4.23.a)
I guess we have two choices, all cash or all commodity. If we stay in cash, we will end the week with \(\$1,000\). But if we go all commodity, then we will have \(\$1,000/$2=500\) ounces of the commodity. So the expected value at the end of the week will be
$$ \evt{money}=\frac12\wts500\wts\$1+\frac12\wts500\wts\$4=\$250+\$1,000=\$1,250 $$
So you’re better off going all in on the commodity.
(4.23.b)
Do not immediately buy but use your money to buy after one week. At that time, the price has either dropped to \(\$1\) so that you can buy a thousand ounces or the price has risen to \(\$4\) so that you can buy 250 ounces. Then
$$ \evt{ounces of commodity}=\frac12\wts1000+\frac12\wts250=500+125=625 $$
(4.24.a)
$$ \evt{B gain if A is 1}=p\wts1+(1-p)\wts\Bop-\frac34\Bcp=p-\frac34+\frac34p=\frac74p-\frac34 $$
(4.24.b)
$$ \evt{B gain if A is 2}=p\wts\Bop-\frac34\Bcp+(1-p)\wts2=-\frac34p+2-2p=-\frac{11}4p+2 $$
(4.25)
- $h,h\qd0.6\wts0.7=0.42$
- $h,t\qd0.6\wts0.3=0.18$
- $t,t\qd0.4\wts0.3=0.12$
- $t,h\qd0.4\wts0.7=0.28$
In [1284]: .4*.3+.6*.3+.4*.7+.6*.7
Out[1284]: 1.0
$$ \pr{X=0}=0.12 $$
$$ \pr{X=1}=0.18+0.28=0.46 $$
$$ \pr{X=2}=0.42 $$
$$ \evw{X}=0\wts0.12+1\wts0.46+2\wts0.42=0.46+0.84=1.3 $$
(4.26.a)
Let $Q$ denote the number of questions asked. It follows that $\pr{Q=i}=\frac1{10}$ and
$$ \evw{Q}=\frac1{10}\sum_{i=1}^{10}i=\frac1{10}\wts55=5.5 $$
(4.26.b)
Write-em down: $1,2,3,4,5,6,7,8,9,10$
- $>5?\qd>3?\qd>1?$
- $>5?\qd>3?\qd>1?\qd>2?$
- $>5?\qd>3?\qd>1?\qd>2?$
- $>5?\qd>3?\qd>4?$
- $>5?\qd>3?\qd>4?$
- $>5?\qd>8?\qd>6?$
- $>5?\qd>8?\qd>6?\qd>7?$
- $>5?\qd>8?\qd>6?\qd>7?$
- $>5?\qd>8?\qd>9?$
- $>5?\qd>8?\qd>9?$
$$ \evw{Q}=3\wts\frac6{10}+4\wts\frac4{10}=\frac95+\frac85=\frac{17}5=3.4 $$
Notice that the Big-O for binary search is very close to the expected value: $\logb{2}{10}\approx3.3219$:
In [1350]: log2(10)
Out[1350]: 3.3219280948873622
Also notice the similarity and difference between this problem and a binary search: say we have an array of $10$ numbers:
$2,5,8,12,16,23,38,56,72,91$
$(02)\qd<16\qd<08\qd<02$
$(05)\qd<16\qd<08\qd<02\qd<05$
$(08)\qd<16\qd<08$
$(12)\qd<16\qd<08\qd<12$
$(16)\qd<16$
$(23)\qd<16\qd<56\qd<23$
$(38)\qd<16\qd<56\qd<23\qd<38$
$(56)\qd<16\qd<56$
$(72)\qd<16\qd<56\qd<72$
$(91)\qd<16\qd<56\qd<72\qd<91$
$$ \evw{Q}=1\wts\frac1{10}+2\wts\frac2{10}+3\wts\frac4{10}+4\wts\frac3{10}=\frac{1+4+12+12}{10}=\frac{29}{10} $$
Alternative write-up:
To eliminate one-half of the remaining numbers, we will ask questions such as “is it greater than or equal to $5.5$?”
Let us keep track of what happens by making a list $(a_1,a_2,…)$, where $a_i$ is the number of numbers that we have not yet determined to be correct or not, when we are asking the $i^{th}$ question. For instance, if the $i^{th}$ question correctly determines the answer, then $a_{i+1}=0$. Note that we are ensured both $a_1=10$ and $a_2=5$.
The answer to our second question will eliminate two or three possibilities, so $a_3=2$ or $3$; moreover $\pr{a_3=2}=\frac25$ and $\pr{a_3=3}=\frac35$.
In the event that $a_3=2$, then we simply ask if one of the two remaining numbers is correct. Then with probability $1$ we will know the correct solution after the third question and $Q=3$.
On the other hand, if $a_3=3$, then we simply ask if one of the three remaining numbers is correct. Then with probability $\frac13$ we will determine the correct number and $Q=3$, and with probability $\frac23$ we will have $a_4=2$, in which case again we will have $Q=4$ with probability $1$.
Putting this together, we have
$$ \evw{Q}=\frac25\wts3+\frac35\Bop\frac13\wts3+\frac23\wts4\Bcp=\frac{17}5=3.4 $$
(4.27)
$\evt{payout}=pA$. So, to make $10\%$ of $A$, we charge the customer $pA+\frac{A}{10}=A\bop p+\frac1{10}\bcp$.
Alternative write-up:
The expected cost is $pA$. Let $P$ denote profit and let $C$ denote the amount we charge a customer if we want expected profit to be $10\%$ of $A$. Then
$$ \frac1{10}A=\evw{P}=C-pA $$
$$ C=pA+\frac1{10}A=A\Bop p+\frac1{10} \Bcp $$
(4.28)
The pmf is
$$ \pr{N=0}=\frac{\binom{16}{3}}{\binom{20}{3}}=\frac{28}{57} $$
$$ \pr{N=1}=\frac{\binom{4}{1}\binom{16}{2}}{\binom{20}{3}}=\frac8{19} $$
$$ \pr{N=2}=\frac{\binom{4}{2}\binom{16}{1}}{\binom{20}{3}}=\frac8{95} $$
$$ \pr{N=3}=\frac{\binom{4}{3}}{\binom{20}{3}}=\frac1{285} $$
So the expected value is
$$ \evw{N}=0\wts\pmf{0}+1\wts\pmf{1}+2\wts\pmf{2}+3\wts\pmf{3} $$
$$ =1\wts\frac8{19}+2\wts\frac8{95}+3\wts\frac1{285} $$
In [1296]: sum([winom(4,i)*winom(16,3-i)/winom(20,3) for i in range(5)])
Out[1296]: 1.00000000000000
In [1297]: sum([i*winom(4,i)*winom(16,3-i)/winom(20,3) for i in range(5)])
Out[1297]: 0.600000000000000
Or we can simply recognize that $\frac4{20}=0.2=20\%$ of any chosen sample will be defective. So
$$ \evw{N}=\frac4{20}\wts3=\frac{12}{20}=0.6 $$
(4.29)
Note: If the first check is negative, we must still check the other possibility.
Some examples
- $p=0.8, 1-p=0.2, C_1=15{,}000, C_2=100$
- $p=0.8, 1-p=0.2, C_1=101, C_2=100$
- $p=0.999, 1-p=0.001, C_1=15{,}000, C_2=100$
In the first case, it obviously make sense to first check the second possible cause since the cost of checking the first possible cause is so expensive.
$$ \frac{15{,}000}{100}=150\quad\quad\frac{p}{1-p}=4 $$
In the second example, the checking costs are about the same but the probabilities favor checking the first possible cause:
$$ \frac{101}{100}=1.01\quad\quad\frac{p}{1-p}=4 $$
In the third case, even though the cost of checking the first possible cause is so high, it still makes sense to check this first since the probability is so much greater than that of the second possible cause:
$$ \frac{15{,}000}{100}=150\quad\quad\frac{p}{1-p}=999 $$
Empirically, we have found that it makes sense to first check the first possible cause when
$$ \frac{C_1}{C_2}\leq\frac{p}{1-p} \tag{4.29.1} $$
Otherwise, it makes sense to check the second possible cause first.
More formally, if we first check the first possible cause, then the expected cost is
$$ \evw{X_1}=C_1+(1−p)C_2+pR_1+(1−p)R_2 $$
Note: If the first check is negative, we must still check the other possibility.
If we first check the second possible cause, then the expected cost is
$$ \evw{X_2}=C_2+pC_1+pR_1+(1−p)R_2 $$
Hence $\evw{X_1}\leq\evw{X_2}$ IFF
$$ C_1+(1−p)C_2+pR_1+(1−p)R_2=\evw{X_1}\leq\evw{X_2}=C_2+pC_1+pR_1+(1−p)R_2 $$
$$ C_1+(1−p)C_2\leq C_2+pC_1 $$
$$ C_1-pC_1\leq C_2-(1−p)C_2 $$
$$ C_1(1-p)\leq C_2\bop1-(1−p)\bcp $$
$$ C_1(1-p)\leq C_2p $$
$$ \frac{C_1}{C_2}\leq\frac{p}{1-p} $$
This matches what we found in (4.29.1).
(4.30)
pmf
- $\pr{X=2}=\frac12$
- $\pr{X=2^2}=\frac1{2^2}=\frac14$
- $\pr{X=2^3}=\frac1{2^3}=\frac18$
- $\pr{X=2^4}=\frac1{2^4}=\frac1{16}$
etc
Checksum:
$$ \sum_{i=1}^{\infty}\pr{X=2^i}=\sum_{i=1}^{\infty}\frac1{2^i}=\sum_{i=0}^{\infty}\frac1{2^i}-\frac1{2^0} =\frac{1}{1-\frac12}-1=\frac1{\frac12}-1=2-1=1 $$
So the expected value is
$$ \evw{X}=\sum_{i=1}^{\infty}2^i\pr{X=2^i}=\sum_{i=1}^{\infty}2^i\frac1{2^i}=\sum_{i=1}^{\infty}1=\infty $$
\(\$1\)million to play a single game?
Note that $2^{19}=524{,}288$ and $2^{20}=1{,}048{,}576$. So we will make less than \(\$1M\) whenever the first tail appears on or before the $19^{th}$ coin toss. Hence
$$ \pr{X<1M}=\sum_{i=1}^{19}\frac1{2^i}=\sum_{i=0}^{19}\frac1{2^i}-\frac1{2^0}=\frac{1-\bop\frac12\bcp^{20}}{1-\frac12}-1=0.99999809265136719 $$
So, no, I wouldn’t play a single game for a million bucks.
(4.30.b)
Intuitively, it certainly makes sense to accept this. We saw in part (a) that we need a game with more than $19$ coin flips to win a million bucks. Similarly we need a game of $30$ or more coin flips to win a billion bucks. If we’re permitted to play indefinitely, then eventually we’ll get a game with $30$ or more coin flips. How many games will we have to play to reach $30$ coin flips? If it’s less than a thousand games, then we make money. And since we don’t have to settle up until we’re done playing, then we should win a lot of money.
I’m not really sure that’s a proof though. Writing out an algo doesn’t seem so simple???????
(4.31)
I don’t understand the problem????????
(4.32)
Quick solution: The given independence assumption tells us that the probability that no one in a given group of $10$ has the disease is $p\equiv\prn{1-\frac1{10}}^{10}$. In this case, there is $1$ test. The probability that at least one person in the group has the disease is $1-p$. In this case, there are $11$ tests. Hence
$$ \evt{number of tests for group i}=1\wts p+11\wts(1-p) $$
In [1910]: p=pw(9/10,10)
In [1911]: p
Out[1911]: 0.34867844010000015
In [1912]: 1*p+11*(1-p)
Out[1912]: 7.5132155989999987
Longer solution: So 10 groups. Let $N_i$ denote the number of tests necessary for group $i$. The desired value is
$$ \evw{N_i}=1\wts p(1)+11\wts p(11) $$
So let’s compute the pmf:
$$ p(1)=\pr{N_i=1}=\prtx{no one in group i has the disease} $$
$$ =\bigcap_{j=1}^{10}\prtx{person j in group i doesn't have the disease} $$
$$ =\prod_{j=1}^{10}\prt{person j in group i doesn't have the disease} \tag{Independence} $$
$$ =\prod_{j=1}^{10}\bop1-\prt{person j in group i has the disease}\bcp $$
$$ =\prod_{j=1}^{10}\Bop1-\frac1{10}\Bcp=\prod_{j=1}^{10}\frac9{10}\approx0.3486784401000001 $$
Notice that for group $i$, there are exactly two disjoint and exhaustive events: no one in the group has the disease or at least one person in the group has the disease. In the former case $N_i=1$ and in the latter case $N_i=11$. Hence
$$ \pmfa{11}{N_i}=1-\pr{N_i=1}=1-\pmf{1} $$
And
$$ \evw{N_i}\approx1\wts0.349+11\wts0.651\approx7.5132155990000005 $$
(4.33)
This solution will closely mirror Example 4b from pages 129-130.
Let $X$ denote the number of newpapers ordered by the newsboy’s 10 customers on a given day. And let $s$ be the number of newspapers stocked by the newsboy on a given day. Then the profit - call it $Q(s)$ - can be expressed as
$$ Q(s)=\cases{5X-10(s-X)&\text{if $X\leq s$}\\5s&\text{if $X>s$}} $$
Let $\pmfa{i}{X}$ be the probability mass function of $X$. Then the expected profit equals
$$ \evw{Q(s)}=\sum_{i=0}^{s}\bop5i-10(s-i)\bcp p(i)+\sum_{i=s+1}^{10}5sp(i) $$
$$ =\sum_{i=0}^{s}\bop5ip(i)-10sp(i)+10ip(i)\bcp+5s\sum_{i=s+1}^{10}p(i) $$
$$ =\sum_{i=0}^{s}\bop5ip(i)+10ip(i)\bcp-\sum_{i=0}^{s}10sp(i)+5s\Bop\sum_{i=0}^{10}p(i)-\sum_{i=0}^{s}p(i)\Bcp $$
$$ =15\sum_{i=0}^{s}ip(i)-10s\sum_{i=0}^{s}p(i)+5s\Bop1-\sum_{i=0}^{s}p(i)\Bcp $$
$$ =15\sum_{i=0}^{s}ip(i)-10s\sum_{i=0}^{s}p(i)+5s-5s\sum_{i=0}^{s}p(i) $$
$$ =5s+15\sum_{i=0}^{s}ip(i)-15s\sum_{i=0}^{s}p(i) $$
Succintly we have
$$ \evw{Q(s)}=5s+15\sum_{i=0}^{s}(i-s)p(i) $$
To determine the optimum value of $s$, let us investigate what happens to the profit when we increase $s$ by $1$ unit. By substitution, we see that the expected profit in this case is given by
$$ \evw{Q(s+1)}=5(s+1)+15\sum_{i=0}^{s+1}(i-(s+1))p(i) $$
$$ =5(s+1)+15\sum_{i=0}^{s}(i-(s+1))p(i) $$
$$ =5(s+1)+15\sum_{i=0}^{s}(i-s-1)p(i) $$
Therefore
$$ \evw{Q(s+1)}-\evw{Q(s)} $$
$$ =5(s+1)+15\sum_{i=0}^{s}(i-s-1)p(i)-\Bop 5s+15\sum_{i=0}^{s}(i-s)p(i) \Bcp $$
$$ =5s+5+15\sum_{i=0}^{s}(i-s)p(i)+15\sum_{i=0}^{s}(-1)p(i)-\Bop 5s+15\sum_{i=0}^{s}(i-s)p(i) \Bcp $$
$$ =5+15\sum_{i=0}^{s}(-1)p(i) $$
Succintly we have
$$ \evw{Q(s+1)}-\evw{Q(s)}=5-15\sum_{i=0}^{s}p(i) $$
Hence
$$ \evw{Q(s+1)}-\evw{Q(s)}>0 \iff \sum_{i=0}^{s}p(i)<\frac13 \tag{4.33.1} $$
And
$$ \evw{Q(s+1)}-\evw{Q(s)}<0 \iff \sum_{i=0}^{s}p(i)>\frac13 \tag{4.33.2} $$
Since $p(i)$ is non-negative, we see that $\sum_{i=0}^{s}p(i)\leq\sum_{i=0}^{s+1}p(i)$ for every $s$.
In words, (4.33.1) says that the expected profit $\evw{Q(s)}$ is increasing in $s$ for any $s$ satisfying $\sum_{i=0}^{s}p(i)<\frac13$. Similarly, (4.33.2) says that the expected profit is decreasing in $s$ for any $s$ satisfying $\sum_{i=0}^{s}p(i)>\frac13$.
Said another way, the expected profit must have a global maximum in $s$.
Let \(s^*\) be the largest value of $s$ satisfying $\sum_{i=0}^{s}p(i)<\frac13$. Then $s^*+1$ must be the global maximum in $s$:
$$ \underbrace{\evw{Q(0)}<\dots<\evw{Q(s^{*})}<}_{\text{follows from 4.33.1}}\evw{Q(s^{*}+1)}\underbrace{>\evw{Q(s^{*}+2)}>\evw{Q(s^{*}+3)}>\dots}_{\text{follows from 4.33.2}} \tag{4.33.3} $$
So it suffices to find \(s^*\). Then \(s^*+1\) will be the desired answer.
Since $X$ is the binomial random variable with parameters $10,\frac13$, then we have $\pmf{i}=\binom{10}{i}\Bop\frac13\Bcp^i\Bop\frac23\Bcp^{10-i}$ and
- $\pmf{0}=\Bop\frac13\Bcp^0\Bop\frac23\Bcp^{10}\approx0.0173415$
- $\pmf{1}=10\Bop\frac13\Bcp^1\Bop\frac23\Bcp^{9}\approx0.0867076$
- $\pmf{2}=45\Bop\frac13\Bcp^2\Bop\frac23\Bcp^{8}\approx0.1950922$
- $\pmf{3}=120\Bop\frac13\Bcp^3\Bop\frac23\Bcp^{7}\approx0.2601229$
$$ \sum_{i=0}^{2}p(i)\approx0.29914\quad\quad\quad\sum_{i=0}^{3}p(i)\approx0.55926 $$
So \(s^*=2\) and \(s^*+1=3\). So the newsboy should purchase \(s^*+1=3\) papers to maximize his expected profit.
(4.35)
$$ \pr{X=\$1.1}=\prt{same}=\frac{\binom52+\binom52}{\binom{10}2}=\frac49 $$
$$ \pr{X=-\$1}=\prt{different}=1-\frac49=\frac59 $$
$$ \evw{X}=\frac{11}{10}\frac49-1\wts\frac59 $$
$$ \evw{X^2}=\Bop\frac{11}{10}\Bcp^2\frac49+(-1)^2\frac59 $$
$$ \varw{X}=\evw{X^2}-\prn{\evw{X}}^2=1.0\overline{8} $$
In [1924]: p=(winom(5,2)+winom(5,2))/winom(10,2)
In [1925]: ex1=1.1*p-1*(1-p)
In [1926]: ex1
Out[1926]: -0.0666666666666667
In [1927]: ex2=pw(1.1,2)*p+1*(1-p)
In [1928]: ex2-pw(ex1,2)
Out[1928]: 1.08888888888889
(4.36)
Recall the mean
$$ \evw{N}=2(p−p^2+1)=2p-2p^2+2 $$
Similarly
$$ \evw{N^2}=2^2p(2)+3^2p(3) $$
$$ =2^2(2p^2−2p+1)+3^2(2p−2p^2) $$
$$ =8p^2−8p+4+18p−18p^2 $$
$$ =-10p^2+10p+4 $$
And the variance is
$$ \varw{N}=\evw{N^2}-\bop\evw{N}\bcp^2 $$
$$ =-10p^2+10p+4-(4p^2-4p^3+4p-4p^3+4p^4-4p^2+4p-4p^2+4) $$
$$ =-10p^2+10p+4-\bop4p^4-8p^3-4p^2+8p+4\bcp $$
$$ =-4p^4+8p^3-6p^2+2p $$
And the first derivative is
$$ 0=\wderiv{\varw{N}}{p}=-16p^3+24p^2-12p+2 $$
In [432]: np.roots([-16,24,-12,2])
Out[432]:
array([ 0.50000247 +4.27037340e-06j, 0.50000247 -4.27037340e-06j,
0.49999507 +0.00000000e+00j])
So $p=\frac12$ is a stationary point.
$$ \wderivn{\varw{N}}{p}{2}\Bop\frac12\Bcp=-48\Bop\frac12\Bcp^2+48\wts\frac12-12=-48\wts\frac14+24-12=-12+12=0 $$
The second derivative test is inconclusive. So is the third derivative:
$$ \wderivn{\varw{N}}{p}{3}\Bop\frac12\Bcp=-96\wts\frac12+48=-48+48=0 $$
But the $4^{th}$ derivative test confirms this is a max:
$$ \wderivn{\varw{N}}{p}{4}\Bop\frac12\Bcp=-96<0 $$
The graph also confirms that $p=\frac12$ is a max:
In [6]: from numpy import array as arr, power as pw, linspace as lnsp
In [7]: import matplotlib.pyplot as plt
In [8]: def graph(funct, x_range):
...: x=arr(x_range)
...: y=funct(x)
...: plt.plot(x,y,'r--')
...: plt.show()
...:
In [9]: graph(lambda p:-4*pw(p,4)+8*pw(p,3)-6*pw(p,2)+2*p, lnsp(0,1,1000))
In [10]: graph(lambda p:-16*pw(p,3)+24*pw(p,2)-12*pw(p,1)+2, lnsp(0,1,1000))
In [11]: graph(lambda p:-48*pw(p,2)+48*pw(p,1)-12, lnsp(0,1,1000))
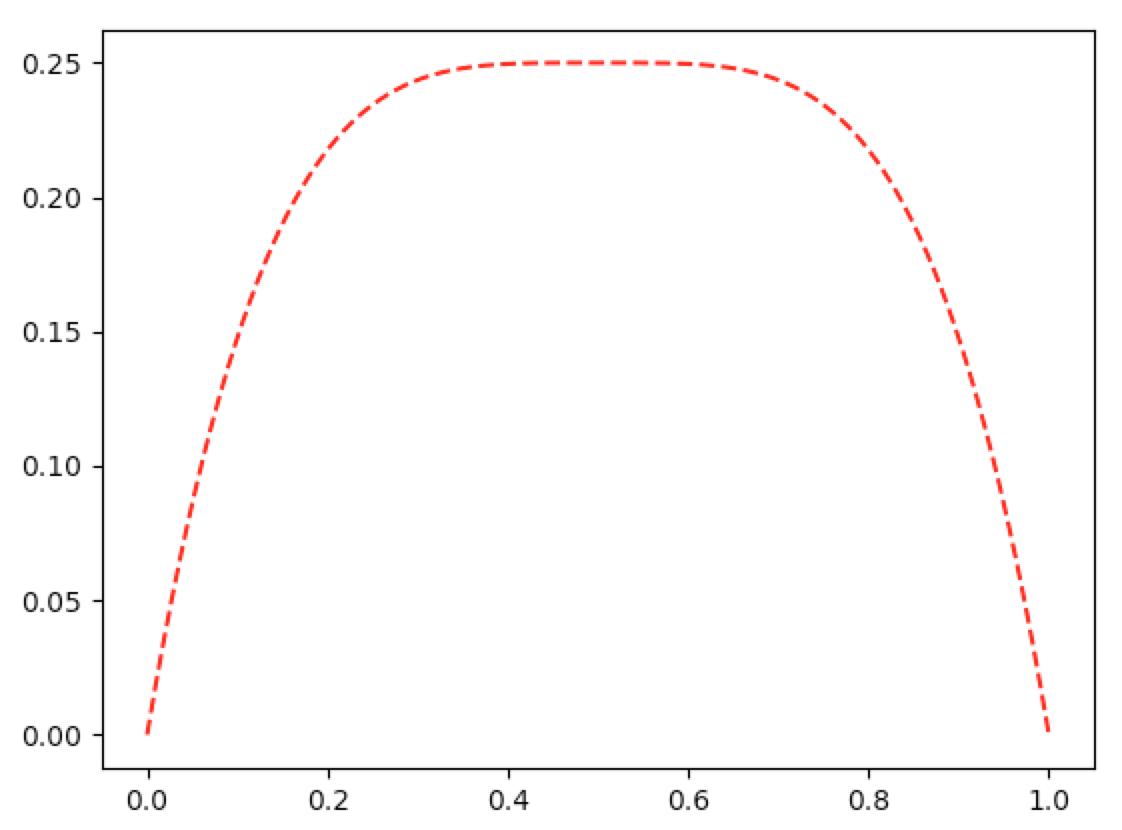
The first derivative:
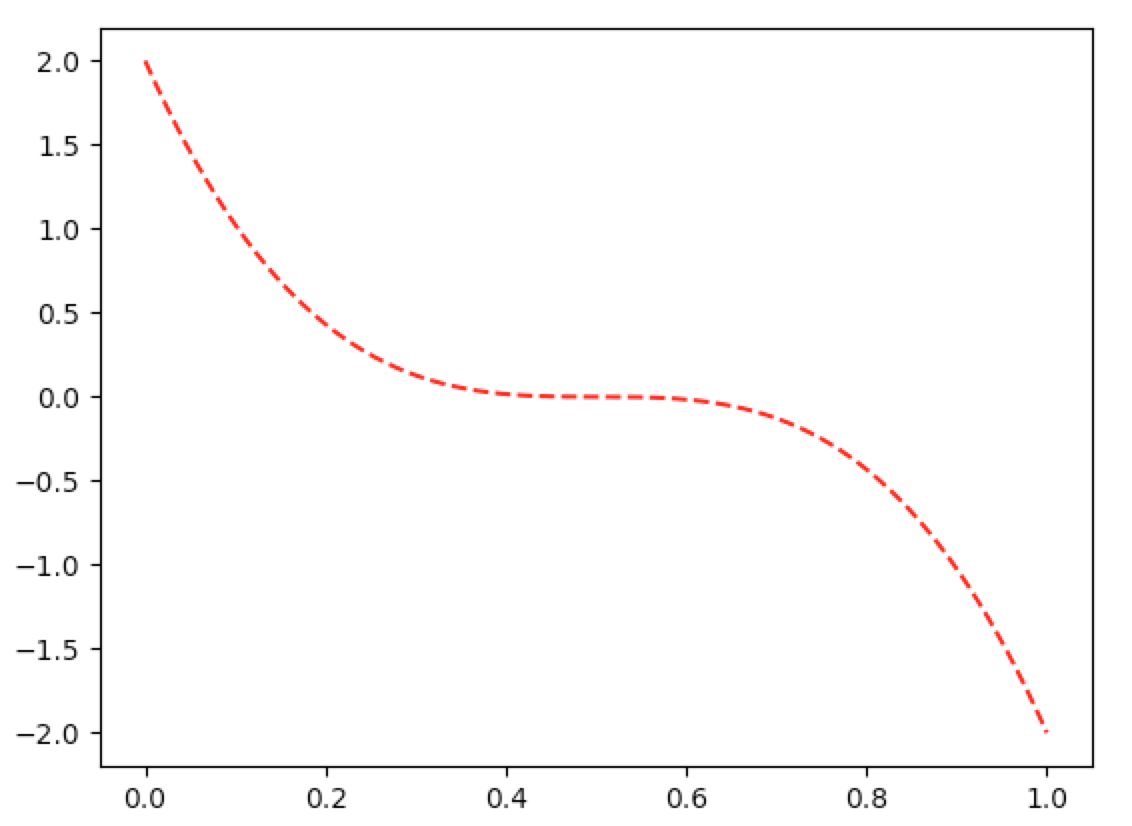
The second derivative:
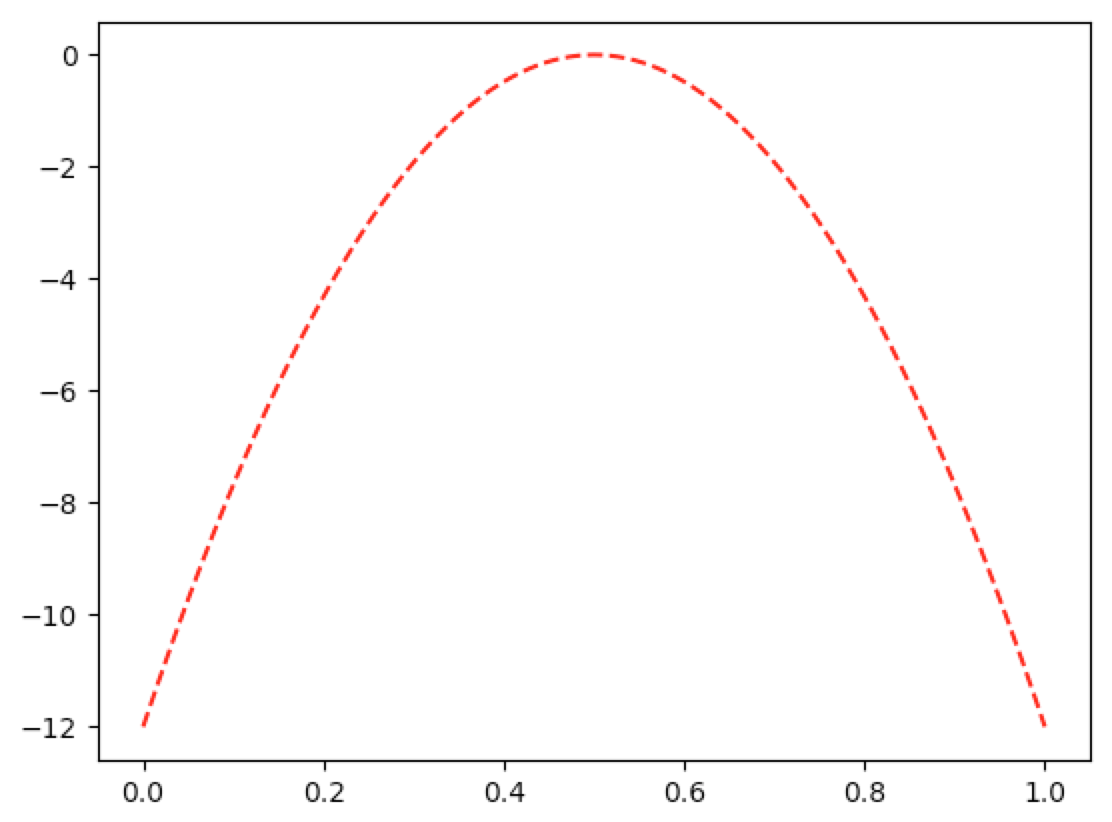
(4.37)
$$ E[Y]=\frac14\wts(40+33+25+50) $$
$$ E[Y^2]=\frac14\wts(40^2+33^2+25^2+50^2) $$
$$ \varw{Y}=E[Y^2]-\bop\evw{Y}\bcp^2 $$
In [1411]: ev=1/4*(pw(40,1)+pw(33,1)+pw(25,1)+pw(50,1))
In [1412]: ev
Out[1412]: 37.0
In [1413]: ev2=1/4*(pw(40,2)+pw(33,2)+pw(25,2)+pw(50,2))
In [1414]: ev2-pw(ev,2)
Out[1414]: 84.5
$$ E[X]=\frac{40^2}{148}+\frac{33^2}{148}+\frac{25^2}{148}+\frac{50^2}{148}=\frac1{148}\wts(40^2+33^2+25^2+50^2) $$
$$ E[X^2]=\frac{40^3}{148}+\frac{33^3}{148}+\frac{25^3}{148}+\frac{50^3}{148}=\frac1{148}\wts(40^3+33^3+25^3+50^3) $$
$$ \varw{X}=\evw{X^2}-\bop\evw{X}\bcp^2 $$
In [1415]: ev=1/148*(pw(40,2)+pw(33,2)+pw(25,2)+pw(50,2))
In [1416]: ev
Out[1416]: 39.283783783783782
In [1417]: ev2=1/148*(pw(40,3)+pw(33,3)+pw(25,3)+pw(50,3))
In [1418]: ev2-pw(ev,2)
Out[1418]: 82.2032505478453
(4.38)
Note that
$$ \evw{X^2}=\varw{X}+\bop\evw{X}\bcp^2=5+1=6 $$
so that
$$ \evw{(2+X)^2}=\evw{X^2+4X+4}=\evw{X^2}+4\evw{X}+4=14 $$
Alternatively:
$$ \evw{(2+X)^2}=\varw{2+X}+\bop\evw{2+X}\bcp^2=\varw{X}+\bop2+\evw{X}\bcp^2=5+3^2=14 $$
$$ \varw{4+3X}=\varw{3X}=9\varw{X}=45 $$
(4.39)
Hypergeometric with replacement is Binomial. Hence
$$ \pr{X=2}=\binom{n}{i}p^i(1-p)^{n-i}=\binom42\Bop\frac36\Bcp^2\Bop1-\frac36\Bcp^{4-2}=6\Bop\frac12\Bcp^4=\frac6{16}=\frac38 $$
Alternatively, we can compute this manually:
- $wwww$
- $wwwb$
- $wwbw$
- $wbww$
- $bwww$
- $wwbb$
- $wbbw$
- $bbww$
- $wbwb$
- $bwbw$
- $bwwb$
- $wbbb$
- $bwbb$
- $bbwb$
- $bbbw$
- $bbbb$
6 out of 16 have two white balls. Replacement implies there are always 3 white balls and 3 black balls. This implies equal probability of drawing a white or black ball at every draw. Hence the probability is 3/8.
We can compute this as
$$ \frac{\binom42}{2^4}=\frac6{16}=\frac38 $$
In the numerator, we choose exactly 2 slots from the available 4. We place 2 white balls in these 2 slots. The 2 remaining slots will be filled in exactly 1 way, with 2 black balls.
In the denominator, each slot has 2 equally likely possibilities.
(4.40)
This is a binomial random variable with parameters $n=5$ and $p=\frac13$.
$$ \pr{X=4}=\binom{n}{i}p^i(1-p)^{n-i}=\binom54\Bop\frac13\Bcp^4\Bop\frac23\Bcp^{5-4}=5\frac1{81}\frac23=\frac{10}{243} $$
$$ \pr{X=5}=\binom{n}{i}p^i(1-p)^{n-i}=\binom55\Bop\frac13\Bcp^5\Bop\frac23\Bcp^{5-5}=\frac1{243} $$
$$ \prt{4 or more correct answers just by guessing}=\pr{X=4}+\pr{X=5}=\frac{11}{243} $$
In [6]: from sympy import binomial as binom, N
In [7]: winom=lambda n,i: N(binom(n,i))
In [8]: from numpy import power as pw
In [9]: brv=lambda n=10,i=0,p=1/2:winom(n,i)*pw(p,i)*pw(1-p,n-i)
In [10]: sum([brv(5,i,1/3) for i in range(4,6)])
Out[10]: 0.0452674897119342
In [11]: 11/243
Out[11]: 0.04526748971193416
(4.41)
This is a binomial random variable with parameters $n=10$ and $p=\frac12$.
$$ \pr{X=7}=\binom{n}{i}p^i(1-p)^{n-i}=\binom{10}7\Bop\frac12\Bcp^7\Bop\frac12\Bcp^{10-7}=120\Bop\frac12\Bcp^{10}=120\frac1{1024} $$
$$ \pr{X=8}=\binom{10}8\frac1{2^{10}}=\frac{45}{1024} $$
$$ \pr{X=9}=\binom{10}9\frac1{1024}=\frac{10}{1024} $$
$$ \pr{X=10}=\binom{10}{10}\frac1{1024}=\frac{1}{1024} $$
$$ \pr{X\geq7}=\frac{120+45+10+1}{1024}=0.171875 $$
from sympy import binomial as binom
from numpy import power as pw
In [464]: rst=[binom(10,i)*pw(1/2,10) for i in range(7,11)]
In [465]: rst
Out[465]:
[0.117187500000000,
0.0439453125000000,
0.00976562500000000,
0.000976562500000000]
In [466]: sum(rst)
Out[466]: 0.171875000000000
(4.42)
Let $N_k$ be the number of engines that don’t fail on a $k$-engine plane.
The probability that a $5$-engine plane completes a successful flight is
$$ \pr{N_5\geq3}=\binom{5}{3}p^3(1-p)^{5-3}+\binom{5}{4}p^4(1-p)^{5-4}+\binom{5}{5}p^5(1-p)^{5-5} $$
$$ =10p^3(1-p)^{2}+5p^4(1-p)+p^5 $$
$$ =10p^3(1-2p+p^2)+5p^4-5p^5+p^5 $$
$$ =10p^3-20p^4+10p^5+5p^4-4p^5 $$
$$ =6p^5-15p^4+10p^3 $$
The probability that a $3$-engine plane completes a successful flight is
$$ \pr{N_3\geq2}=\binom{3}{2}p^2(1-p)^{3-2}+\binom{3}{3}p^3(1-p)^{3-3} $$
$$ =3p^2(1-p)+p^3 $$
$$ =3p^2-3p^3+p^3 $$
$$ =3p^2-2p^3 $$
Obviously a $5$-engine plane will be preferable to a $3$-engine plane when the probability that it will complete a successful flight is greater than that of a $3$-engine plane. That is $\pr{N_5\geq3}>\pr{N_3\geq2}$. So
$$ 0<\pr{N_5\geq3}-\pr{N_3\geq2}=6p^5-15p^4+10p^3-\bop3p^2-2p^3\bcp $$
$$ =6p^5-15p^4+10p^3-3p^2+2p^3 $$
$$ =6p^5-15p^4+12p^3-3p^2 $$
That is
$$ 0<6p^3-15p^2+12p-3=6\Bop p-\frac12\Bcp(p-1)^2 \tag{4.42.1} $$
So $p>\frac12$. Note: I don’t understand the factorization in 4.42.1. Saw this in the solutions manual. I see that it works but how does one intuitively see that $\frac12$ and $1$ are roots without Calculus?
In [1976]: apc=lambda n=5,p=1/2: sum([brv(n,i,p) for i in range(int(np.ceil(n/2)),n+1)])
In [1977]: def eng5or3(wr):
...: ra=[]
...: for p in wr:
...: if apc(5,p)>=apc(3,p):
...: ra.append(p)
...: return ra
...:
In [1978]: eng5or3(lnsp(0,1,11))
Out[1978]:
[0.0,
0.5,
0.60000000000000009,
0.70000000000000007,
0.80000000000000004,
0.90000000000000002,
1.0]
(4.43)
$$ \prt{wrong decoded message}=\prt{minority of bits decoded correctly} $$
$$ =\prt{0 bits decoded correctly}+\prt{1 bit decoded correctly}+\prt{2 bits decoded correctly} $$
$$ =\binom50\Bop\frac45\Bcp^0\Bop\frac15\Bcp^{5-0}+\binom51\Bop\frac45\Bcp^1\Bop\frac15\Bcp^{5-1}+\binom52\Bop\frac45\Bcp^2\Bop\frac15\Bcp^{5-2} $$
In [1430]: sum([brv(5,i,4/5) for i in range(0,3)])
Out[1430]: 0.0579200000000000
To model this as a binomial random variable, we are assuming that digit transmittion accuracy is independent. That is, the probability of transmitting any two bits successfully is independent.
Alternatively:
$$ \prt{wrong decoded message}=\prt{majority of bits decoded incorrectly} $$
$$ =\prt{3 bits decoded incorrectly}+\prt{4 bits decoded incorrectly}+\prt{5 bits decoded incorrectly} $$
$$ =\binom530.2^30.8^2+\binom540.2^40.8^1+\binom550.2^50.8^0 $$
In [482]: bst=[binom(5,i)*pw(0.2,i)*pw(0.8,5-i) for i in range(3,6)]
In [483]: bst
Out[483]: [0.0512000000000000, 0.00640000000000000, 0.000320000000000000]
In [484]: sum(bst)
Out[484]: 0.0579200000000000
(4.44)
Let $F$ denote the event that the satellite system functions tomorrow. And let $R$ denote the event that it rains tomorrow. Then
$$ \pr{F}=\cond{F}{R} $$
$$ =\alpha\sum_{i=k}^{n}\binom{n}{i}p_1^i(1-p_1)^{n-i}+(1-\alpha)\sum_{i=k}^{n}\binom{n}{i}p_2^i(1-p_2)^{n-i} $$
(4.45)
Let $Q_e$ denote the event that the student passes the exam with $e$ examiners. And let $D$ denote the event that the student has an “on” day. Then
$$ 2\pr{D}=\pr{D^c}=1-\pr{D}\iff3\pr{D}=1\iff\pr{D}=\frac13 $$
and
$$ \pr{Q_3}=\cond{Q_3}{D} $$
$$ =\frac13\sum_{i=2}^{3}\binom3i0.8^i0.2^{3-i}+\frac23\sum_{i=2}^{3}\binom3i0.4^i0.6^{3-i} $$
In [492]: st31=[binom(3,i)*pw(0.8,i)*pw(0.2,3-i) for i in range(2,4)]
In [493]: st32=[binom(3,i)*pw(0.4,i)*pw(0.6,3-i) for i in range(2,4)]
In [494]: (1/3)*sum(st31)+(2/3)*sum(st32)
Out[494]: 0.533333333333333
$$ \pr{Q_5}=\cond{Q_5}{D} $$
$$ =\frac13\sum_{i=3}^{5}\binom5i0.8^i0.2^{5-i}+\frac23\sum_{i=3}^{5}\binom5i0.4^i0.6^{5-i} $$
In [497]: st51=[binom(5,i)*pw(0.8,i)*pw(0.2,5-i) for i in range(3,6)]
In [498]: st52=[binom(5,i)*pw(0.4,i)*pw(0.6,5-i) for i in range(3,6)]
In [499]: (1/3)*sum(st51)+(2/3)*sum(st52)
Out[499]: 0.525653333333333
or
In [1992]: apc=lambda n=5,p=1/2: sum([brv(n,i,p) for i in range(int(np.ceil(n/2)),n+1)])
In [1993]: (2/3)*apc(n=5,p=4/10)+(1/3)*apc(n=5,p=8/10)
Out[1993]: 0.525653333333333
In [1994]: (2/3)*apc(n=3,p=4/10)+(1/3)*apc(n=3,p=8/10)
Out[1994]: 0.533333333333333
(4.46)
Let $Q$ denote the event that the jury renders a correct decision. And let $G$ denote the event that the defendant is guilty. Then
$$ \pr{Q}=\cond{Q}{G} $$
$$ =0.65\sum_{i=9}^{12}\binom{12}{i}0.8^i0.2^{12-i}+0.35\sum_{i=4}^{12}\binom{12}{i}0.9^i0.1^{12-i} \tag{4.46.1} $$
In [532]: jr1=[binom(12,i)*pw(0.8,i)*pw(0.2,12-i) for i in range(9,13)]
In [533]: jr2=[binom(12,i)*pw(0.9,i)*pw(0.1,12-i) for i in range(4,13)]
In [534]: 0.65*sum(jr1)+0.35*sum(jr2)
Out[534]: 0.866469759301751
Note that the first term in 4.46.1 is the percentage of guilty defendants who are convicted. To find the percentage of defendants convicted, we need to account for those innocent defendants who are convicted. Let $C$ denote the event that the defendant is convicted:
$$ \cp{C}{G}\pr{G}+\cp{C}{G^c}\pr{G^c} $$
$$ =0.65\sum_{i=9}^{12}\binom{12}{i}0.8^i0.2^{12-i}+0.35\sum_{i=0}^{3}\binom{12}{i}0.9^i0.1^{12-i} $$
In [1440]: 0.65*sum([brv(12,i,4/5) for i in range(9,13)])+0.35*sum([brv(12,i,9/10) for i in range(0,4)])
Out[1440]: 0.516469875386250
In [1441]: sum([brv(12,i,9/10) for i in range(0,4)])
Out[1441]: 1.65835000000000e-7
In [1442]: sum([brv(12,i,1/10) for i in range(9,13)]) # check
Out[1442]: 1.65835000000000e-7
(4.48)
The probability that a single pack of $10$ contains more than $1$ defective disk is
$$ p\equiv\sum_{i=2}^{10}\binom{10}{i}0.01^i0.99^{10-i} $$
In [1461]: p=sum([brv(10,i,1/100) for i in range(2,11)])
In [1462]: p
Out[1462]: 0.00426620024283142
In [1463]: 1-sum([winom(10,i)*pw(1/100,i)*pw(1-1/100,10-i) for i in range(0,2)]) #check
Out[1463]: 0.00426620024283164
$$ \prt{exactly 1 of 3 packs is returned}=\binom{3}{1}p^1(1-p)^{3-1} $$
In [1464]: brv(3,1,p)
Out[1464]: 0.0126896308819010
In [1465]: winom(3,1)*pw(p,1)*pw(1-p,3-1) #check
Out[1465]: 0.0126896308819010
(4.49.a)
Let $Q_i$ denote the event that coin $i$ is chosen. Let $H$ denote the event that the chosen coin lands on heads exactly $7$ times in the ten flips. Then
$$ \pr{H}=\condi{H}{Q_1}+\condi{H}{Q_2} $$
$$ =\frac12\binom{10}70.4^70.6^{10-7}+\frac12\binom{10}70.7^70.3^{10-7} $$
In [550]: 0.5*binom(10,7)*pw(0.4,7)*pw(0.6,3)+0.5*binom(10,7)*pw(0.7,7)*pw(0.3,3)
Out[550]: 0.154647630000000
(4.49.b)
Let $F$ denote the event that the first of these ten flips lands on heads. And let $G$ denote the event that the chosen coin lands on heads exactly $6$ times on flips $2$ through $10$. Then
$$ \cp{H}F=\frac{\pr{HF}}{\pr{F}}=\frac{\pr{GF}}{\pr{F}} $$
Initially, I tried this
$$ \frac{\pr{GF}}{\pr{F}}=\frac{\pr{G}\pr{F}}{\pr{F}}=\pr{G} $$
But Professor Ross said “your solution is wrong because F and G are not independent events. (they are conditionally ind given the coin selected)”. The second half of this answer is a good explanation of dependent but conditionally independent.
In problem (3.39), I discuss unconditionally dependent and conditionally independent in detail. This situation is identical, and is a great example. Let’s say the first of the $10$ flips is heads. This makes it more likely that the second coin was chosen. This in turn increases the probability that we will get heads on $6$ of the remaining $9$ flips.
That is, the occurrence of $F$ increases the probability of the occurrence of $G$. Hence $F$ and $G$ are unconditionally dependent.
But if we know that coin $1$ was chosen, then the occurrence of $F$ tells us nothing about the probability of the occurrence of $G$ since flipping coin $1$ presumably has independent results. The same goes for the case where we know that coin $2$ was chosen.
That is, $F$ and $G$ are conditionally independent. So we just condition the numerator on the chosen coin:
$$ \pr{GF}=\condi{GF}{Q_1}+\condi{GF}{Q_2} $$
$$ =\frac12\Bocb\cp{GF}{Q_1}+\cp{GF}{Q_2}\Bccb $$
$$ =\frac12\Bocb\cp{G}{Q_1}\cp{F}{Q_1}+\cp{G}{Q_2}\cp{F}{Q_2}\Bccb \tag{4.49.b.1} $$
$$ =\frac12\Bocb \binom960.4^60.6^30.4+\binom960.7^60.3^30.7 \Bccb $$
$$ =\frac12\Bocb \binom960.4^70.6^3+\binom960.7^70.3^3 \Bccb $$
Notice that we used conditional independence in 4.49.b.1. The denominator can also be conditioned on the coin:
$$ \pr{F}=\condi{F}{Q_1}+\condi{F}{Q_2}=\frac12\Bop 0.4+0.7 \Bcp=0.55 $$
So that
$$ \cp{H}F=\frac{\frac12\Bocb \binom960.4^70.6^3+\binom960.7^70.3^3 \Bccb}{0.55} $$
In [589]: (1/2)*( binom(9,6)*pw(.4,7)*pw(.6,3)+binom(9,6)*pw(.7,7)*pw(.3,3) ) / (0.55)
Out[589]: 0.196824256363636
(4.50.a)
$$ \cpstc{H,T,T}{6 heads}=\frac{\prt{HTT & 6 heads}}{\prt{6 heads}} $$
$$ =\frac{\cpstc{6 heads}{HTT}\prt{HTT}}{\prt{6 heads}} $$
$$ =\frac{\prt{5 heads on last 7 flips}\prt{HTT}}{\prt{6 heads}} $$
$$ =\frac{\binom75p^5q^2pq^2}{\binom{10}{6}p^6q^4} $$
$$ =\frac{\binom75}{\binom{10}{6}}=\frac1{10} $$
(4.50.b)
$$ \cpstc{T,H,T}{6 heads}=\frac{\prt{THT & 6 heads}}{\prt{6 heads}} $$
$$ =\frac{\cpstc{6 heads}{THT}\prt{THT}}{\prt{6 heads}} $$
$$ =\frac{\prt{5 heads on last 7 flips}\prt{THT}}{\prt{6 heads}} $$
$$ =\frac{\binom75p^5q^2pq^2}{\binom{10}{6}p^6q^4} $$
$$ =\frac{\binom75}{\binom{10}{6}}=\frac1{10} $$
(4.51.a)
Let $X$ denote the number of typographical errors on the next page of a certain magazine.
$$ \lambda=\evw{X}=0.2 $$
Note that
- $n$ (number of characters per page) is large, say $700$
- the probability that each character is a typo is small: $p=\frac\lambda{n}\approx\frac{.2}{700}\approx.0003$
- typos are independent
Hence we can compute the number of typos on the next page as a Binomial random variable or we can approximate this as a Poisson random variable:
$$ \pmfa{0}{X}=\binom{700}0p^0(1-p)^{700} $$
In [2040]: n,lam=700,.2
In [2041]: p=lam/n
In [2042]: n,p,lam
Out[2042]: (700, 0.00028571428571428574, 0.2)
In [2043]: brv(n,0,p)
Out[2043]: 0.818707356648391
In [2044]: winom(n,0)*pw(p,0)*pw(1-p,n-0)
Out[2044]: 0.818707356648391
Poisson Approximation:
$$ \pmfa{0}{X}=\frac{\e{-\lambda}\lambda^0}{0!}=\e{-.2} $$
In [2045]: exp(-lam)
Out[2045]: 0.81873075307798182
(4.51.b)
$$ \pr{X\geq2}=1-\bop\pr{X=0}+\pr{X=1}\bcp=1-\bop\e{-.2}+.2\e{-.2}\bcp=1-1.2\e{-.2} $$
In [2046]: 1-(brv(n,0,p)+brv(n,1,p)),1-(exp(-lam)+lam*exp(-lam))
Out[2046]: (0.0175043753739372, 0.017523096306421793)
(4.52.a)
Let $X$ denote the number of worldwide airplane crashes of commercial airlines for the next month.
$$ \lambda=\evw{X}=3.5 $$
Note that
- $n$ (number of commercial flights per month) is large, say $70{,}000$
- the probability that each flight ends in crash is small: $p=\frac\lambda{n}\approx\frac{3.5}{70{,}000}\approx0.00005$
- crashes are independent
Hence we can compute the number of crashes in the next month as a Binomial random variable or we can approximate this as a Poisson random variable:
$$ \pmfa{0}{X}=\binom{70{,}000}0p^0(1-p)^{70{,}000} $$
$$ \pmfa{1}{X}=\binom{70{,}000}1p^1(1-p)^{70{,}000-1} $$
$$ \pr{X\geq2}=1-\bop\pr{X=0}+\pr{X=1}\bcp $$
In [1587]: n=70000
In [1588]: p=3.5/n
In [1589]: p
Out[1589]: 5e-05
In [1590]: p0=winom(n,0)*pw(p,0)*pw(1-p,n)
In [1591]: p1=winom(n,1)*pw(p,1)*pw(1-p,n-1)
In [1592]: p0,p1,1-(p0+p1)
Out[1592]: (0.0301947411788058, 0.105686878469744, 0.864118380351450)
Poisson Approximation:
$$ \pmfa{0}{X}=\frac{\e{-\lambda}\lambda^0}{0!}=\e{-3.5} $$
$$ \pmfa{1}{X}=\frac{\e{-\lambda}\lambda^1}{1!}=3.5\e{-3.5} $$
$$ \pr{X\geq2}=1-\bop\pr{X=0}+\pr{X=1}\bcp=1-\bop\e{-3.5}+3.5\e{-3.5}\bcp=1-4.5\e{-3.5} $$
In [1593]: p0=exp(-3.5)
In [1594]: p1=3.5*exp(-3.5)
In [1595]: p0,p1,1-(p0+p1)
Out[1595]: (0.030197383422318501, 0.10569084197811475, 0.86411177459956678)
(4.52.b)
$$ \pr{X\leq1}=\pr{X=0}+\pr{X=1}=e^{-3.5}+3.5e^{-3.5}=4.5e^{-3.5} $$
(4.53.a)
Let $X$ denote the number of couples where both were born on Apr 30. Let’s assume that every individual has an equal chance of having been born on any given date.
Let’s also assume that the birthdays of the $160{,}000$ individuals are independent. It follows that the birthdays of any subset of the $160{,}000$ individuals are independent. In particular, the two birthdays of any given couple are independent.
Hence, for any given couple, the probability that $0,1,$ or $2$ of the two individuals has an Apr 20 bday is a Binomial random variable:
$$ \pmfa{i}{X}=\binom2i\Prn{\frac1{365}}^{i}\Prn{1-\frac1{365}}^{2-i} $$
Then the probability that an arbitrary couple were both born on April 30 is $p=\bop\frac1{365}\bcp^2$. Checksum:
In [1638]: n,p=2,1/365
In [1639]: n,p
Out[1639]: (2, 0.0027397260273972603)
In [1640]: sum([brv(n,i,p) for i in range(0,3)])
Out[1640]: 1.00000000000000
In [1641]: binom(2,0)*pw(1/365,0)*pw(1-1/365,2)+binom(2,1)*pw(1/365,1)*pw(1-1/365,1)+binom(2,2)*pw(1/365,2)*pw(1-1/365,0)
Out[1641]: 1.00000000000000
Note that
- $n$ (number of marriages per month) is large, $80{,}000$
- the probability that each couple shares Apr 30 bday is small: $p=\bop\frac1{365}\bcp^2$
- shared Apr 30 bdays are independent from couple-to-couple
Hence we can compute the number of shared Apr 30 bdays as a Binomial random variable or we can approximate this as a Poisson random variable:
$$ \pmfa{0}{X}=\binom{80{,}000}0p^0(1-p)^{80{,}000} $$
$$ \prt{at least 1 couple where both born on Apr 30}=\pr{X\geq1}=1-\pr{X=0} $$
In [1610]: n=80000
In [1611]: p=pw(1/365,2)
In [1612]: winom(n,0)*pw(p,0)*pw(1-p,n)
Out[1612]: 0.548542701939118
In [1613]: 1-winom(n,0)*pw(p,0)*pw(1-p,n)
Out[1613]: 0.451457298060882
In [2055]: sum([brv(n,i,p) for i in range(1,80001)]) # this takes a long time to compute, 45 mins
Out[2055]: 0.451457298065054
For the Poisson approximation, we first compute $\lambda$:
$$ \text{mean}=\text{expected value}=\lambda=np=\frac{80{,}000}{365^2}\approx.6 $$
And compute the probability that no couples were both born on Apr 30:
$$ \pmfa{0}{X}=\frac{\e{-\lambda}\lambda^0}{0!}=\e{−\lambda} $$
Then the probability that at least one couple were both born on Apr 30 is approximately
$$ \pr{X\geq1}=1-\pr{X=0}=1-p(0)=1-e^{−\lambda} $$
In [1614]: lam=n*p
In [1615]: lam
Out[1615]: 0.60048789641583789
In [1616]: exp(-lam),1-exp(-lam)
Out[1616]: (0.5485439381735443, 0.4514560618264557)
(4.53.b)
The probability that an arbitrary couple were born on the same day is $p=\binom22\frac{365\wts1}{365^2}=\frac1{365}$. Checksum:
In [1649]: winom(2,0)*365*364/pw(365,2)+winom(2,2)/365
Out[1649]: 1.00000000000000
$$ \pmfa{0}{X}=\binom{80{,}000}0p^0(1-p)^{80{,}000} $$
$$ \prt{at least 1 couple with same bday}=\pr{X\geq1}=1-\pr{X=0} $$
In [1642]: n=80000
In [1643]: p=1/365
In [1644]: winom(n,0)*pw(p,0)*pw(1-p,n)
Out[1644]: 4.80325237872427e-96
In [1645]: 1-winom(n,0)*pw(p,0)*pw(1-p,n)
Out[1645]: 1.00000000000000
For the Poisson approximation, we first compute $\lambda$:
$$ \text{mean}=\text{expected value}=\lambda=np=\frac{80{,}000}{365}\approx219 $$
And compute the probability that no couples were born on the same day:
$$ \pmfa{0}{X}=\frac{\e{-\lambda}\lambda^0}{0!}=\e{−\lambda} $$
Then the probability that at least one couple were both born on the same day is approximately
$$ \pr{X\geq1}=1-\pr{X=0}=1-p(0)=1-e^{−219}=1 $$
In [1655]: n,p=80000,1/365
In [1656]: lam=n*p
In [1657]: n,p,lam
Out[1657]: (80000, 0.0027397260273972603, 219.17808219178082)
In [1658]: exp(-lam),1-exp(-lam)
Out[1658]: (6.4888591902831896e-96, 1.0)
(4.54)
Let $X$ be the number of abandoned cars on this highway in the next week.
$$ \lambda=\evw{X}=2.2 $$
Because $n$ (number of cars driving on this highway) is large (say $44{,}000$), the probability that each car being abandoned is small ($p=\frac\lambda{n}\approx\frac{2.2}{44{,}000}\approx.00005$), and abandonments are independent, we can either compute the probability of this Binomial RV:
$$ \pmfa{0}{X}=\binom{44{,}000}0p^0(1-p)^{44{,}000} $$
Or we can approximate the number of abandonments in a week as a Poisson distribution:
$$ \pmfa{0}{X}=\frac{\e{-\lambda}\lambda^0}{0!}=\e{-2.2} $$
$$ \pr{X\geq2}=1-\prn{\pr{X=0}+\pr{X=1}}=1-\prn{\e{-2.2}+2.2\e{-2.2}}=1-3.2\e{-2.2} $$
In [1664]: n,lam=44000,2.2
In [1665]: p=lam/n
In [1666]: n,p,lam
Out[1666]: (44000, 5e-05, 2.2)
In [1667]: brv(n,0,p),exp(-lam)
Out[1667]: (0.110797064153101, 0.11080315836233387)
In [1668]: 1-(brv(n,0,p)+brv(n,1,p)),1-(exp(-lam)+lam*exp(-lam))
Out[1668]: (0.645437206423605, 0.64542989324053157)
(4.55)
Let $X$ be the number of typos when typed by the first typist. And let $Y$ be the number of typos when typed by the second typist.
$$ \lambda_X=\evw{X}=3\quad\quad\quad\lambda_Y=\evw{Y}=4.2 $$
$$ \pr{X=0}=\frac{e^{-\lambda}\lambda^0}{0!}=e^{-3}\dq\pr{Y=0}=\frac{e^{-\lambda}\lambda^0}{0!}=e^{-4.2} $$
Let $Z$ be the number of typos when typed by the pool of typists. And let $T_X$ be the event that typist $X$ is selected. Then we condition on the selected typist:
$$ \pr{Z=0}=\condi{Z}{T_X}+\condi{Z}{T_Y} $$
$$ =\pr{X=0}\frac12+\pr{Y=0}\frac12=\frac12\prn{\e{-3}+\e{-4.2}} $$
In [1674]: n,lamx,lamy=42000,3,4.2
In [1675]: px,py=lamx/n,lamy/n
In [1676]: n,px,py,lamx,lamy
Out[1676]: (42000, 7.142857142857143e-05, 0.0001, 3, 4.2)
In [1677]: 1/2*(brv(n,0,px)+brv(n,0,py)),1/2*(exp(-lamx)+exp(-lamy))
Out[1677]: (0.0323870809704269, 0.032391322594170824)
(4.56)
Let $X_n$ denote the number of people in the group of size $n$ who share my birthday.
$$ \pr{X_n\geq1}=1-\pr{X_n=0} $$
$$ \pr{X_1=0}=\frac{364}{365}\quad\quad\quad \pr{X_1=1}=\frac1{365} $$
$$ \pr{X_2=0}=\frac{364^2}{365^2}\quad\quad\quad \pr{X_2=1}=\frac{\binom21364\wt1}{365^2} \quad\quad\quad \pr{X_2=2}=\frac{1}{365^2} $$
$$ \pr{X_3=0}=\frac{364^3}{365^3}\dq \pr{X_3=1}=\frac{\binom31364^2}{365^3} \dq \pr{X_3=2}=\frac{\binom32364}{365^3} \dq \pr{X_3=3}=\frac{1}{365^3} $$
In [1698]: sum([binom(3,i)*pw(1/365,i)*pw(1-1/365,3-i) for i in range(0,4)])
Out[1698]: 1.00000000000000
In [1699]: sum([brv(3,i,1/365) for i in range(0,4)])
Out[1699]: 1.00000000000000
$$ \pr{X_n=0}=\frac{364^n}{365^n} \dq\dots\dq \pr{X_n=i}=\frac{\binom{n}{i}364^{n-i}}{365^n} \dq\dots\dq \pr{X_n=n}=\frac{1}{365^n} $$
In [1729]: bdayc=lambda n=10,p=1/365,lst=0: ( lambda l: (sum(l),l[:lst]) if lst else sum(l) ) ([brv(n,i,p) for i in range(0,n+1)])
In [1730]: bdayc(4,lst=4)
Out[1730]:
(1.00000000000000,
[0.989086050280368,
0.0108690774756084,
4.47901544324524e-5,
8.20332498762863e-8])
In [1731]: bdayc(253,lst=5)
Out[1731]:
(1.00000000000000,
[0.499522845963418,
0.347195824254794,
0.120183169934352,
0.0276245198292328,
0.00474322112452487])
In [1732]: bdayc(252,lst=5)
Out[1732]:
(1.00000000000000,
[0.500895161474307,
0.346773573328367,
0.119560668826126,
0.0273719479913293,
0.00468105429247321])
Now we want to find how many people are needed so that the probability that at least one of them has the same birthday as me is greater than $\frac12$. That is, we want to find the smallest $n$ such that $\pr{X_n\geq1}>\frac12$. This is equivalent to finding the smallest $n$ such that $\pr{X_n=0}<\frac12$.
We computed this in python just above to be $n=253$. We see that $\pr{X_{252}=0}\approx0.5009>\frac12$. But $\pr{X_{253}=0}\approx0.4995<\frac12$. More directly, we have
In [1733]: def find_bday_n():
...: prev_n0,curr_n0,i=bdayc(2,lst=1)[1][0],.0,3
...: while(True):
...: curr_n0=bdayc(i,lst=1)[1][0]
...: if curr_n0 < 1/2:
...: return (i,curr_n0,i-1,prev_n0)
...: prev_n0=curr_n0
...: i+=1
...:
In [1734]: find_bday_n()
Out[1734]: (253, 0.499522845963418, 252, 0.500895161474307)
Now let’s compute this analytically, first as a Binonimal random variable:
$$ \frac12<\pr{X_n\geq1}=1-\pr{X_n=0}=1-\Prn{\frac{364}{365}}^n $$
$\iff$
$$ \Prn{\frac{364}{365}}^n<1-\frac12 $$
$\iff$
$$ n\ln\Prn{\frac{364}{365}}=\ln\Cbr{\Prn{\frac{364}{365}}^n}<\ln\Prn{\frac12} $$
$\iff$
$$ n>\frac{\ln\prn{\frac12}}{\ln\prn{\frac{364}{365}}}\approx252.652 $$
Before we approximate this, let’s note that
- $n$ - the number of people needed - is the unknown but should be somewhat large
- the probability $p=\frac1{365}$ is small that one of them shares my bday
- all birthdays are independent
So the Poisson approximation should be good. First compute $\lambda$:
$$ \lambda_n=\evw{X_n}=np=\frac{n}{365} $$
And the Poisson distribution gives us
$$ \pr{X_n=0}=\frac{\e{-\lambda_n}\lambda_n^0}{0!}=\e{-\frac{n}{365}} $$
$$ \frac12<\pr{X_n\geq1}=1-\pr{X_n=0}=1-\e{-\frac{n}{365}} $$
$$ \e{-\frac{n}{365}}<1-\frac12 $$
$$ -\frac{n}{365}<\ln\Prn{\frac12} $$
$$ n>-365\wts\ln\Prn{\frac12}\approx252.9987 $$
(4.58)
In [1744]: prv_np=lambda n=10,i=1,p=1/10: exp(-n*p)*pw(n*p,i)/wf(i)
In [1745]: brv_vs_prv=lambda n=10,i=1,p=1/10: (brv(n,i,p),prv_np(n,i,p))
$i=2,n=8,p=.1$
In [1746]: brv_vs_prv(n=8,i=2,p=.1)
Out[1746]: (0.148803480000000, 0.14378526851751092)
$i=9,n=10,p=.95$
In [1747]: brv_vs_prv(n=10,i=9,p=.95)
Out[1747]: (0.315124704862305, 0.13000253969226788)
$i=0,n=10,p=.1$
In [1748]: brv_vs_prv(n=10,i=0,p=.1)
Out[1748]: (0.348678440100000, 0.36787944117144233)
$i=4,n=9,p=.2$
In [1749]: brv_vs_prv(n=9,i=4,p=.2)
Out[1749]: (0.0660602880000001, 0.072301733708121971)
(4.59)
$$ \lambda=np=50\wts\frac1{100}=\frac12 $$
$$ \pr{X\geq1}=1-\pmf{0}=1-\frac{\e{-\lambda}\lambda^0}{0!}=1-\e{-\frac12} $$
In [1755]: 1-(brv(50,0,1/100)),1-(exp(-50*1/100))
Out[1755]: (0.394993932862464, 0.39346934028736658)
$$ \pmfa{1}{X}=\frac{\e{-\lambda}\lambda^1}{1!}=\frac12\e{-\frac12} $$
$$ \pr{X\geq2}=1-\prn{\pmf{0}+\pmf{1}}=1-\Prn{\e{-\frac12}+\frac12\e{-\frac12}}=1-\frac32\e{-\frac12} $$
In [1757]: n,p=50,1/100
In [1758]: 1-(brv(n,0,p)+brv(n,1,p)),1-(exp(-n*p)+n*p*exp(-n*p))
Out[1758]: (0.0894353130960310, 0.090204010431049864)
(4.60)
Let $B$ denote the event that the drug is beneficial. Let $C$ denote the event of $2$ colds in that year.
$$ \cp{B}{C}=\frac{\condi{C}{B}}{\pr{C}} $$
$$ \cp{C}{B}=\frac{e^{-3}3^2}{2!}=\frac92e^{-3} $$
$$ \pr{C}=\cond{C}B $$
$$ =\frac{9}2e^{-3}\frac34+\frac{25}2e^{-5}\frac14 $$
$$ \cp{B}{C}=\frac{\frac92e^{-3}\frac34}{\frac{9}2e^{-3}\frac34+\frac{25}2e^{-5}\frac14}\approx0.8886 $$
In [1767]: p2gb=exp(-3)*pw(3,2)/2
In [1768]: pb=3/4
In [1769]: p2gbc=exp(-5)*pw(5,2)/2
In [1770]: p2gb*pb/(p2gb*pb+p2gbc*(1-pb))
Out[1770]: 0.88864366475381573
(4.61)
- $n=1{,}000$ is large
- $p\approx0.0014406$ is small
- assume independence of deals
$$ n=1000\dq p\approx0.0014406\dq\lambda=np\approx1.4406 $$
$$ \pr{X\geq2}=1-\prn{\pr{X=0}+\pr{X=1}} $$
$$ =1-\Prn{\e{-1.4406}+1.4406\wts\e{-1.4406}} $$
$$ =1-2.4406\wts\e{-1.4406}\approx0.4221 $$
In [1806]: n=1000
In [1807]: p=winom(13,1)*winom(4,3)*winom(12,1)*winom(4,2)/winom(52,5)
In [1808]: lam=float(n*p)
In [1809]: n,p,lam
Out[1809]: (1000, 0.00144057623049220, 1.4405762304921967)
In [1810]: 1-(brv(n,0,p)+brv(n,1,p)),1-(exp(-lam)+lam*exp(-lam))
Out[1810]: (0.422201164689220, 0.42209284750258347)
Full house computation: see my problem set just after pr.2.15.e: the section Example 5g
(4.63)
We are given that the unit of time is $2$ minutes and that $\lambda=1$. Let $t$ units of time be the duration of interest and let $N(t)$ denote the number of people entering the casino in $t$ units of time. Then by equation (7.5), we have
$$ \pr{N(t)=k}=e^{-\lambda t}\frac{(\lambda t)^k}{k!}=e^{-t}\frac{t^k}{k!} $$
With $t=2.5$ (i.e. $5$ minutes) and $k=0$, we get
$$ \pr{N(2.5)=0}=e^{-2.5}\frac{2.5^0}{0!}=e^{-2.5} $$
Similarly
$$ \pr{N(2.5)\geq4} $$
$$ =1-\prn{\pr{N(2.5)=0}+\pr{N(2.5)=1}+\pr{N(2.5)=2}+\pr{N(2.5)=3}} $$
$$ =1-\prn{\e{-2.5}+2.5\e{-2.5}+\frac{2.5}{2}\e{-2.5}+\frac{2.5^3}{3!}\e{-2.5}} $$
In [1834]: prvt=lambda lam=1,t=2,i=0: exp(-float(lam*t))*pw(lam*t,i)/wf(i)
In [1835]: 1-sum([prvt(t=2.5,i=i) for i in range(0,4)])
Out[1835]: 0.24242386686693407
(4.64.a)
We are given that the unit of time is $1$ month and that $\lambda=4$ for a city of $400{,}000$ inhabitants. Let $t$ units of time be the duration of interest and let $N(t)$ denote the number of suicides in $t$ units of time. Then by equation (7.5), we have
$$ \pr{N(t)=k}=e^{-\lambda t}\frac{(\lambda t)^k}{k!}=e^{-4t}\frac{(4t)^k}{k!} $$
With $t=1$ (i.e. $1$ month), we get
$$ p\equiv \pr{N(1)\geq8}=1-\sum_{k=0}^{7}e^{-4}\frac{4^k}{k!} $$
In [745]: slt=[exp(-4)*pw(4,i)/wf(i) for i in range(0,8)]
In [746]: 1-sum(slt)
Out[746]: 0.051133615792847475
(4.64.b)
In a given year, let $X$ denote the number of months wherein there will be at least $8$ suicides. For a given month, we just computed the probability of at least $8$ suicides to be $p\approx0.051$. Since we have presumed independence of suicide numbers from month-to-month, we see that $X$ is a binomial random variable with parameters $n=12$ and $p\approx0.051$. Hence
$$ \pr{X=0}=\binom{12}0p^0(1-p)^{12}=(1-p)^{12} $$
$$ \pr{X=1}=\binom{12}1p^1(1-p)^{11}=12p(1-p)^{11} $$
Thus
$$ \pr{X\geq2}=1-\prn{\pr{X=0}+\pr{X=1}} $$
$$ =1-\prn{(1-p)^{12}+12p(1-p)^{11}}\approx0.123 $$
Or do the Poisson approximation:
$$ \pr{X\geq2}=1-\prn{\pr{X=0}+\pr{X=1}}=1-\prn{\e{-np}+np\wts\e{-np}} $$
In [1837]: n,p=12,1-sum([exp(-4)*pw(4,i)/wf(i) for i in range(0,8)])
In [1838]: n,p
Out[1838]: (12, 0.051133615792847475)
In [1839]: 1-(pw(1-p,12)+12*p*pw(1-p,11))
Out[1839]: 0.12286327329457203
In [1840]: 1-(exp(-n*p)+n*p*exp(-n*p))
Out[1840]: 0.12640079259567871
Aside:
$$ \binom{n}ip^i(1-p)^{n-i}\approx\frac{\e{-np}(np)^i}{i!} $$
(4.64.c)
Let’s first compute the probability that the third month from now will be the first to have at least $8$ suicides. That means that this month and next month must have less than $8$. So the probability is $p(1-p)^2$.That is, $2$ failures and $1$ success must occur. Similarly
$$ \prt{month $i$ is the first month with at least 8}=p(1-p)^{i-1} $$
Fun exercise:
import random
def flip(p):
return (random.random()<p)
def flip3(p=.9):
return (flip(p),flip(p),flip(p))
flt3=[(1 if flip3(.9)==(True,True,False) else 0,1) for i in range(0,1000000)]
sum([pair[0] for pair in flt3])/sum([pair[1] for pair in flt3])
Out[849]: 0.080888000000000002
Of course we should expect $2$ successes followed by a failure about $0.9\wts0.9\wts0.1=8.1\%$ of the time.
(4.65.a)
$n=500$ is large, $p=0.001$ is small, and we have independence. Hence we can approximate with Poisson. Let $X$ denote the number of soldiers with the disease. Let $B$ denote the event of a positive company blood test. And set $\lambda=np=.5$. Then
$$ \pr{B}=\prt{at least 1 soldier has the disease} $$
$$ =\pr{X\geq1}=1-\pr{X=0}=1-\e{-.5}\frac{.5^0}{0!}=1-\e{-.5} $$
Of course we can compute this exactly as well:
In [1841]: n,p=500,1e-3
In [1842]: 1-exp(-n*p),1-winom(n,0)*pw(p,0)*pw(1-p,500)
Out[1842]: (0.39346934028736658, 0.393621055138815)
(4.65.b)
$$ \cp{X\geq2}{X\geq1}=\frac{\pr{X\geq2\cap X\geq1}}{\pr{X\geq1}} $$
$$ =\frac{\pr{X\geq2}}{1-\e{-.5}}=\frac{1-\pr{X<2}}{1-\e{-\frac12}} $$
$$ =\frac{1-\prn{\pr{X=0}+\pr{X=1}}}{1-\e{-\frac12}} $$
$$ =\frac{1-\prn{\e{-\frac12}+\frac12\e{-\frac12}}}{1-\e{-\frac12}} $$
$$ =\frac{1-\frac32e^{-\frac12}}{1-e^{-\frac12}} $$
or
$$ \cp{X>1}{B}=1-\cp{X=1}{B} $$
$$ =1-\frac{\cp{B}{X=1}\pr{X=1}}{\pr{B}} $$
$$ =1-\frac{\frac12e^{-\frac12}}{1-e^{-\frac12}} $$
$$ =\frac{1-\frac32e^{-\frac12}}{1-e^{-\frac12}} $$
In [1844]: (1-(brv(n,0,p)+brv(n,1,p)))/(1-brv(n,0,p)),(1-(exp(-n*p)+n*p*exp(-n*p)))/(1-exp(-n*p))
Out[1844]: (0.228971719287329, 0.22925295873160084)
(4.65.c)
Let $J$ denote the event that Jones has the disease. Then
$$ J\cap\set{X\geq1}=J\dq\text{since }J\subset\set{X\geq1} $$
That is, from Jones’ point of view, the positive company test reveals no new information:
$$ \cp{X\geq2}{J\cap\set{X\geq1}}=\cp{X\geq2}{J} $$
Hence, from Jones’ point of view, the probability that more than one person has the disease, given a positive company test, is equal to the unconditional probability that at least one of the remaining $499$ people has the disease. Thus the problem is the same as (a), but with $499$ people instead of $500$.
So we let $Y$ be the number of people in this reduced group that has the disease. Using the Poisson approximation again and setting $\lambda=np=\frac{499}{10^3}$, we get
$$ \prt{at least 1 soldier in the remaining 499 has the disease} $$
$$ =\pr{Y\geq1}=1-\pr{Y=0}=1-e^{-.499}\frac{.499^0}{0!}=1-e^{-.499} $$
In [27]: 1-exp(-.499)
Out[27]: 0.39286250626121033
(4.65.d)
The idea is the same as in part (c). Once the authorities find the positive individual test, this can explain the positive company test. So the probability that any of the remaining soldiers have the disease is just the unconditional probability that any of the remaining have it. Again we do Poisson approximation and set $\lambda=np=\frac{500-i}{10^3}$:
$$ \prt{at least 1 soldier in the remaining 500-i has the disease} $$
$$ =\pr{Z\geq1}=1-\pr{Z=0}=1-e^{-\frac{500-i}{10^3}}\frac{\Bop\frac{500-i}{10^3}\Bcp^0}{0!}=1-e^{-\frac{500-i}{10^3}} $$
Computing the Binonmial random variable, we have
$$ \pr{Z\geq1}=1-\pr{Z=0}=1-\binom{500-i}{0}p^0(1-p)^{500-i}=1-(1-p)^{500-i} $$
Here’s a snippet to show the approximation error:
from numpy import *
from matplotlib.pylab import *
i = arange(500)
p = 1.0/1000
p_poisson = 1 - exp( - p*(500 - i) )
p_binom = 1 - exp( (500 - i) * log(1-p) )
subplot(211)
plot(i, p_poisson, '-b', label="Poisson")
plot(i, p_binom, '--r', label="Binomial")
legend()
subplot(212)
plot(i, p_binom - p_poisson , '-b', label="Binomial - Poisson")
legend()
show()
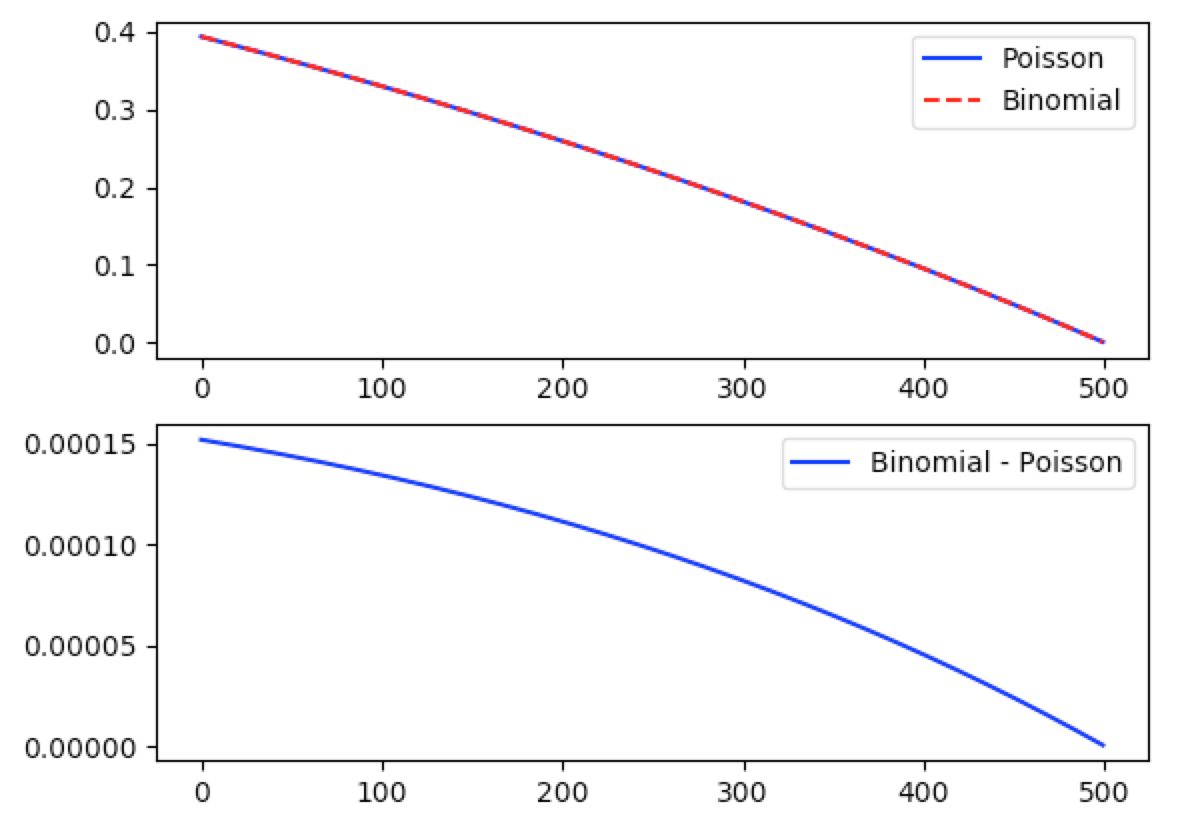
In the top plot, it appears that the graphs of the Poisson approximation and Binomial are very close, if not identical. In the bottom plot, we actually see the graph of the error. Looking at the scale of the error, we see that the numbers are very small relative to the numbers from the top plot. Specifically, $\frac{0.00015}{0.3}=0.0005$. In this case, we say that the error is several orders of magnitude less than the values themselves. Hence the Poisson approximation is good.
(4.66.a)
From problem (2.43.b), we know that there are $(2n-1)!$ ways for the $2n$ people to sit around the round table. Now fix the $i^{th}$ couple, male on the left, in two of the seats. Since this effectively breaks the circle, the other $2n-2$ people can sit in $(2n-2)!$ ways around the table. The same count applies with the female of couple $i$ on the left. Hence
$$ \pr{C_i}=\frac{2(2n-2)!}{(2n-1)!}=\frac{2}{2n-1} $$
Alternative view: consider the $i^{th}$ couple, male on the left, as one person. Then there are $2n-1$ people to sit around the table. Hence a count of $(2n-2)!$. Same goes for the female of the $i^{th}$ couple on the left.
Original, convoluted solution:
Suppose $n=2$. So we have $2$ couples and $4$ people. Hence there are $4!$ permutations of seatings. We designate females with odd numbers and males with even numbers. We designate couple $i$ with the numbers $1,2$. We designate $i^{th}$ couple together with female on the left with purple. And we designate $i^{th}$ couple together with female on the right with red. Black denotes that $i^{th}$ couple are not seated together.
- $\color{purple}{1234}$
- $\color{purple}{1243}$
- $1324$
- $\color{red}{1342}$
- $\color{red}{1432}$
- $1423$
- $\color{red}{2134}$
- $\color{red}{2143}$
- $2314$
- $\color{purple}{2341}$
- $2413$
- $\color{purple}{2431}$
- $\color{purple}{3124}$
- $3142$
- $\color{red}{3214}$
- $3241$
- $\color{purple}{3412}$
- $\color{red}{3421}$
- $\color{purple}{4123}$
- $4132$
- $\color{red}{4213}$
- $4231$
- $\color{purple}{4312}$
- $\color{red}{4321}$
There are $(2n)!$ possible seatings.
Fix couple $i$. And, for the moment, fix the permutation of the seating of the other non-$i$ couples. Not the particular seats they’re sitting in, but the order amongst themselves without regard for couple $i$. And let’s consider how many ways couple $i$ can sit together with the lady on the left.
Then lady $i$ can be in seats $1,2,…,2n$ and the man can be in corresponding seats $2,3,…,1$. This is the count of all the ways that couple $i$ can be seated together with the lady on the left and with a fixed permutation of the non-$i$ couples. This count is $2n$.
Now consider the same case but count all permutations of the members of the non-$i$ couples. For each possible seating of couple $i$ together, lady on the left, there are $(2n-2)!$ possible seatings of the others. Hence there are $2n\bop(2n-2)!\bcp$ possible seating of couple $i$ together, lady on the left.
Hence altogether (lady or man on the left) there are $4n\bop(2n-2)!\bcp$ possible seatings of couple $i$ next to each other. Thus
$$ \pr{C_i}=\frac{4n\bop(2n-2)!\bcp}{(2n)!}=\frac{4n}{2n(2n-1)}=\frac{2}{2n-1} $$
(4.66.b)
We can regard couple $i$ sitting together as breaking the circle. That is, another couple can no longer sit together in tail-head form because couple $i$ breaks the circle.
Hence the question now involves a row of $2n−2$ people. These can be arranged in $(2n−2)!$ ways.
If we treat couple $j$ sitting together as a single person, then there are $(2n-3)!$ possible permutations. We then double that count as they can sit either way round. Hence
$$ \cp{C_j}{C_i}=\frac{2(2n-3)!}{(2n-2)!}=\frac2{2n-2}=\frac1{n-1} $$
Alternative solution: Put couple $j$ in the first two seats of the broken circle. The others can sit $(2n-4)!$ ways. Now flip couple $j$ in the same seats. So we have a count of $2(2n-4)!$ for couple $j$ sitting in seats $1$ and $2$. Now move couple $j$ to seats $2$ and $3$. Same count of $2(2n-4)!$.
Etc until couple $j$ sit in seats $(2n-3)$ and $(2n-2)$. So thats a total count of
$$ 2(2n-3)\prn{(2n-4)!}=2(2n-3)! $$
(4.66.c)
Let $X$ denote the number of couples seated next to each other. We wish to compute $\pr{X=0}$.
For large $n$, $\pr{C_i}$ is small. To use a Poisson approximation, we must show independence or almost independence of the events $C_j$, $j=1,2,…,n$. For large $n$, we have
$$ \cp{C_j}{C_i}=\frac2{2n-2}\approx\frac2{2n-1}=\pr{C_j} $$
Note that $\lambda=n\wts\pr{C_i}=\frac{2n}{2n-1}$. Alternatively, we can compute $\lambda=\evw{X}$: Let $I_i$ denote the indicator random variable for couple $i$. That is
$$ I_i=\cases{1&\text{if couple $i$ is seated next to each other}\\0&\text{not seated next to each other}} $$
Then
$$ \evw{I_i}=0\wts\pr{C_i^c}+1\wts \pr{C_i}=\pr{C_i} $$
Note that $X=\sum_{i=1}^nI_i$. Hence
$$ \lambda=\evw{X}=\evwB{\sum_{i=1}^nI_i}=\sum_{i=1}^n\evw{I_i}=\sum_{i=1}^n\pr{C_i} $$
$$ =\sum_{i=1}^n\frac2{2n-1}=n\frac2{2n-1}=\frac{2n}{2n-1} $$
With $\lambda$ computed, we can now compute
$$ \prt{no couples sitting together}=\pr{X=0}=e^{-\lambda}=e^{-\frac{2n}{2n-1}}\approx e^{-1} $$
In [2244]: circpc=lambda n=10: (2/(2*n-1),2/(2*n-2),brv(n,0,2/(2*n-1)),exp(-n*2/(2*n-1)))
In [2245]: circpc()
Out[2245]:
(0.10526315789473684,
0.1111111111111111,
0.328816198631666,
0.34901807093131998)
In [2246]: circpc(100)
Out[2246]:
(0.010050251256281407,
0.010101010101010102,
0.364179063850309,
0.36603543781817888)
In [2247]: circpc(1000)
Out[2247]:
(0.0010005002501250625,
0.001001001001001001,
0.367511347011224,
0.36769545545826321)
(4.67.a)
We will represent female-male alternating by odd-even alternating. That is, women are $1,3,5$ and men are $2,4,6$. Let’s write some examples.
Suppose $n=2$. So we have $2$ couples and $4$ people.
- $\color{purple}{1234}$
- $\color{red}{1432}$
- $\color{red}{2143}$
- $\color{purple}{2341}$
- $\color{red}{3214}$
- $\color{purple}{3412}$
- $\color{purple}{4123}$
- $\color{red}{4321}$
Suppose $n=3$. So we have $3$ couples and $6$ people.
- $\color{purple}{123456}$
- $\color{purple}{123654}$
- $\color{purple}{125634}$
- $\color{purple}{125436}$
- $\color{purple}{412365}$
- $\color{purple}{412563}$
- $\color{purple}{612345}$
- $\color{purple}{612543}$
- $\color{purple}{341256}$
- $\color{purple}{361254}$
- $\color{purple}{541236}$
- $\color{purple}{561234}$
- $\color{purple}{436125}$
- $\color{purple}{456123}$
- $\color{purple}{634125}$
- $\color{purple}{654123}$
- $\color{purple}{345612}$
- $\color{purple}{365412}$
- $\color{purple}{543612}$
- $\color{purple}{563412}$
- $\color{purple}{234561}$
- $\color{purple}{254361}$
- $\color{purple}{236541}$
- $\color{purple}{256341}$
There are $4n(n-1)^2(n-2)^2\dots2^2$ possible seatings with $1,2$ together and odd-even alternating. That is, with couple $i$ together and woman-man alternating.
To see this, first fix the permutation of the non-$i$ couples (just the ordering, not the seats). The lady $i$ can be in seats $1,2,…,2n$ and the man can be in corresponding seats $2,3,…,1$. This is the count of all the ways that couple $i$ can be seated together with the lady on the left and with a fixed permutation of the non-$i$ couples. This count is $2n$. With the lady or man on the left, the count is $4n$.
Now we fix $1,2$ in the first and second positions, we have $n-1=2$ choices for the third position. That is, to fill the third position, we must select an odd number, so we can only select from $3$ or $5$. We cannot select $4$ or $6$ because these are even (male). Similarly, for the fourth position, we can only select from $4$ or $6$, which is also $n-1$ choices.
For the next two positions, we can only select from $n-2$ choices, etc.
Overall, there are $2n^2(n-1)^2\dots2^2$ possible seatings with woman-man alternating.
$$ \pr{C_i}=\frac{4n(n-1)^2(n-2)^2\dots2^2}{2n^2(n-1)^2\dots2^2}=\frac{2}{n} $$
(4.67.b)
The $i^{th}$ couple seated together effectively breaks the cirlce. So we are left with a row of $(2n-2)!$ people. For these $n-1$ couples and female-male alternating order, first consider female-first. There are $(n-1)^2(n-2)^2\dots2^2$ possible seatings. So for male or female first, there are $2(n-1)^2(n-2)^2\dots2^2$ possible seatings with male-female alternating.
Disregarding couple $j$ for the moment, the other $n-2$ couples can be seated in $2(n-2)^2(n-3)^2\dots2^2$ permutations. We can then put the conjoined $j^{th}$ couple in any of $2n-3$ slots. That is, with the $n-2$ couples, there are $2n-4$ people lined up in a row and there are $2n-4+1=2n-3$ slots to place the conjoined $j^{th}$ couple. So for the number of seating permutations with male-female alternating, couple $i$ seated together, and couple $j$ seated together, there’s a total count of $2(2n-3)(n-2)^2(n-3)^2\dots2^2$.
$$ \cp{C_j}{C_i}=\frac{2(2n-3)(n-2)^2(n-3)^2\dots2^2}{2(n-1)^2(n-2)^2\dots2^2}=\frac{2n-3}{(n-1)^2} $$
(4.67.c)
For large $n$, $\pr{C_i}$ is small. We also have weak dependence for large $n$:
$$ \cp{C_j}{C_i}=\frac{2n-3}{(n-1)^2}=\frac{2n-3}{n^2-2n+1}=\frac{\frac1n(2n-3)}{\frac1n(n^2-2n+1)}=\frac{2-\frac3n}{n-2+\frac1n}\approx\frac2n $$
And we can compute $\lambda$:
$$ \lambda=\evw{\text{number of couples seated next to each other}}=\evwB{\sum_{i=1}^nI_i} $$
$$ =\sum_{i=1}^n\evw{I_i}=\sum_{i=1}^n\pr{C_i}=\sum_{i=1}^n\frac2n=n\frac2n=2 $$
With $\lambda$ computed, we can now compute
$$ \prt{no couples sitting together}=\pr{X=0}=e^{-\lambda}=e^{-2} $$
(4.68)
Poisson Paradigm. Consider $n$ events, with $p_i$ equal to the probability that event $i$ occurs, $i = 1,…,n$. If all the $p_i$ are “small” and the trials are either independent or at most “weakly dependent,” then the number of these events that occur approximately has a Poisson distribution with mean $\sum_{i=1}^np_i$.
????????
(4.69.a)
The probability of each permutation of the ten flips is $p\equiv pw(.5,10)=0.0009765625$. So we just need to count the number of permutations with $4$ consecutive heads.
Let $N_i$ denote the event that $4$ consecutive heads starts at position $i$. Then we have
- $N_1=2^6\quad[HHHHwwwwww]$
- $N_2=2^5\quad[THHHHwwwww]$
- $N_3=2^5\quad[wTHHHHwwww]$
- $N_4=2^5\quad[wwTHHHHwww]$
- $N_5=2^5\quad[wwwTHHHHww]$
- $N_6=2^5−2\quad[wwwwTHHHHw]\text{ minus }[HHHHTHHHHw]$
- $N_7=2^5−3\quad[wwwwwTHHHH]\text{ minus }([HHHHwTHHHH]\text{ or }[THHHHTHHHH])$
$$ N\equiv\sum_{i=1}^{7}N_i=2^6+6\wts2^5-5=64+192-5=251 $$
So the probability of four consecutive flips is $Np=251\wts0.0009765625=0.2451171875$.
We can also use the formula from example 7d, Length of the longest run, page 151:
In [217]: n,k,p=10,4,.5
In [218]: sum([pw(-1,r+1)*(binom(n-r*k,r)+(1/p)*binom(n-r*k,r-1))*pw(p,k*r)*pw(1-p,r) for r in range(1,n-k+1)])
Out[218]: 0.245138514786959
(4.69.b)
The recursive formula is also given on page 151:
$$ P_n=\sum_{j=1}^{k}P_{n-j}p^{j-1}(1-p)+p^k $$
In [283]: wict={}
In [284]: def P_n(p=.5,n=10,k=4):
...: global wict
...: if n in wict:
...: return wict[n]
...: if k>n:
...: return 0.0
...: s=pw(p,k)
...: for i in range(1,k+1):
...: s+=P_n(p=p,n=n-i,k=k)*pw(p,i-1)*(1-p)
...: wict[n]=s
...: return s
...:
In [285]: P_n()
Out[285]: 0.2451171875
(4.69.c)
Let $A_n$ denote the event that there is a string of $4$ consecutive heads in a sequence of $n$ flips of a fair coin. Then
$$ \lambda=\evw{A_{10}}=0\wts \pr{A_{10}^c}+1\wts P_{10} $$
Let $B_n$ denote the longest run of consecutive heads for $n$ flips.
$$ \lambda=\evw{B_{10}}=0\wts P_0+1\wts P_1+\dots+10\wts P_{10}=\sum_{i=0}^{10}iP_i $$
Let $I_i$ denote the indicator variable that flip $i$ ended a string of exactly $4$ consecutive heads.
$$ \lambda=\evw{C_{10}}= $$
?????????
(4.78)
The probability of choosing $2$ white and $2$ black balls on any given round is
$$ p\equiv\frac{\binom42\binom42}{\binom84} $$
In [1862]: p=winom(4,2)*winom(4,2)/winom(8,4)
In [1863]: p
Out[1863]: 0.514285714285714
Let $X$ denote the number of rounds required to choose $2$ and $2$. Then
$$ \pr{X=n}=(1-p)^{n-1}p $$
$X$ is a geometric random variable. To get the expected number of rounds, we recall example 8b where it is computed $\evw{X}=\frac1p$.