Cauchy-Schwarz Inequality
Proposition W.6.CS.1 The order of orthogonality doesn’t matter. Let $u,v\in V$ with $\innprd{v}{u}=0$. Then conjugate symmetry (6.3, p.166) gives the first equality:
$$ \innprd{u}{v} = \overline{\innprd{v}{u}} = \overline{0} = 0\quad\blacksquare $$
Proposition W.6.CS.2 Scaling preserves orthogonality. Let $u,v\in V$ with $\innprd{u}{v}=0$ and let $\lambda\in\mathbb{F}$. Then homogeneity in the first slot gives the first equality:
$$ \innprd{\lambda u}{v} = \lambda\innprd{u}{v}=0 $$
and similarly
$$ \innprd{u}{\lambda v} = \overline{\innprd{\lambda v}{u}} = \overline{\lambda \innprd{v}{u}} = \overline{\lambda\cdot0} = \overline{0}=0\quad\blacksquare $$
Proposition W.6.CS.3 Orthogonal decomposition: Let $u,v\in V$ with $v\neq0$. Also let $\lambda\in\mathbb{F}$. Then $\lambda v$ and $u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v$ are orthogonal:
$$\begin{align*} \innprdBg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}{\lambda v} &= \innprd{u}{\lambda v}+\innprdBg{-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}{\lambda v}\tag{by additivty in first slot, 6.3} \\ &= \innprd{u}{\lambda v}+\Prngg{-\frac{\innprd{u}{v}}{\dnorm{v}^2}}\innprd{v}{\lambda v}\tag{by homogeneity in first slot, 6.3} \\ &= \innprd{u}{\lambda v}-\frac{\innprd{u}{v}}{\dnorm{v}^2}\innprd{v}{\lambda v} \\ &= \overline{\lambda}\innprd{u}{v}-\overline{\lambda}\Prn{\frac{\innprd{u}{v}}{\dnorm{v}^2}}\innprd{v}{v}\tag{by 6.7.e} \\ &= \overline{\lambda}\innprd{u}{v}-\overline{\lambda}\Prn{\frac{\innprd{u}{v}}{\dnorm{v}^2}}\dnorm{v}^2\tag{by norm definition, 6.8} \\ &= \overline{\lambda}\innprd{u}{v}-\overline{\lambda}\innprd{u}{v} \\ &= 0\quad\blacksquare \end{align*}$$
Proposition W.6.CS.4 Norm positivity: Let $v\in V$. Then positivity of the inner product (6.3) gives $\innprd{v}{v}\geq0$ and
$$ \dnorm{v}=\sqrt{\innprd{v}{v}}\geq0\quad\blacksquare $$
Proposition W.6.CS.5 Zero norm: Let $v\in V$. The definiteness of the inner product (6.3) means that
$$ \innprd{v}{v}=0\quad\iff\quad v=0 $$
Hence
$$ \dnorm{v}=\sqrt{\innprd{v}{v}}=0\quad\iff\quad v=0\quad\blacksquare $$
Then proposition W.6.CS.3 gives that $\frac{\innprd{u}{v}}{\dnorm{v}^2}v$ and $u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v$ are orthogonal and the Pythagorean Theorem gives the second equality:
$$\begin{align*} \dnorm{u}^2 &= \dnormBgg{\frac{\innprd{u}{v}}{\dnorm{v}^2}v+u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2 \\ &= \dnormBgg{\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2 \\ &= \Prngg{\normBgg{\frac{\innprd{u}{v}}{\dnorm{v}^2}}\dnorm{v}}^2+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2\tag{by 6.10.b} \\ &= \Prngg{\frac{\normb{\innprd{u}{v}}}{\normb{\dnorm{v}^2}}\dnorm{v}}^2+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2\tag{by multiplicativity of absolute value, 4.5} \\ &= \Prngg{\frac{\normb{\innprd{u}{v}}}{\dnorm{v}^2}\dnorm{v}}^2+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2\tag{by norm positivity, W.6.CS.4} \\ &= \Prngg{\frac{\normb{\innprd{u}{v}}}{\dnorm{v}}}^2+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2 \\ &= \frac{\normb{\innprd{u}{v}}^2}{\dnorm{v}^2}+\dnormBgg{u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v}^2 \\ &\geq \frac{\normb{\innprd{u}{v}}^2}{\dnorm{v}^2}\tag{by norm positivity, W.6.CS.4} \\ \end{align*}$$
Multiplying both sides of this inequality by $\dnorm{v}^2$ and then taking square roots gives the Cauchy-Schwarz inequality.
Note that proposition W.6.CS.5 implies that equality holds if and only if $0=u-\frac{\innprd{u}{v}}{\dnorm{v}^2}v$.
Suppose $u$ is a scalar multiple of $v$. Then
$$\begin{align*} \normb{\innprd{u}{v}}=\normb{\innprd{\lambda v}{v}}=\norm{\lambda}\normb{\innprd{v}{v}}=\norm{\lambda}\normb{\dnorm{v}^2}=\norm{\lambda}\dnorm{v}^2=\norm{\lambda}\dnorm{v}\dnorm{v}=\dnorm{\lambda v}\dnorm{v}=\dnorm{u}\dnorm{v} \end{align*}$$
Now suppose that $\normb{\innprd{u}{v}}=\dnorm{u}\dnorm{v}$ and $v\neq0$. ???
And here is the Cauchy-Schwarz in inner product form:
$$ \normb{\innprd{u}{v}}\leq\sqrt{\innprd{u}{u}}\sqrt{\innprd{v}{v}}=\sqrt{\innprd{u}{u}\innprd{v}{v}} $$
6.22, Parallelogram Equality
$$\begin{align*} \dnorm{u+v}^2+\dnorm{u-v}^2 &= \innprd{u+v}{u+v}+\innprd{u-v}{u-v} \\ &= \innprd{u}{u+v}+\innprd{v}{u+v}+\innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &+ \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &+ \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= 2\innprd{u}{u}+2\innprd{v}{v} \\ &= 2\prn{\dnorm{u}^2+\dnorm{v}^2} \\ \end{align*}$$
6.31, p.183 Gram-Schmidt Procedure
Define
$$ c_j\equiv\dnorm{v_j-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}} $$
For $k=1,\dots,j-1$, we have
$$\begin{align*} \innprd{e_j}{e_k} &= \innprdBgg{\frac{v_j-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}{\dnorm{v_j-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}}}{e_k} \\ &= \innprdBgg{\frac{v_j-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}{c_j}}{e_k} \\ &= \frac1{c_j}\innprdbg{v_j-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}{e_k} \\ &= \frac1{c_j}\Prn{\innprdbg{v_j}{e_k}+\innprdbg{-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}{e_k}} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}+\frac1{c_j}\innprdbg{-\innprd{v_j}{e_1}e_1-\dotsb-\innprd{v_j}{e_{j-1}}e_{j-1}}{e_k} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}+\frac1{c_j}\sum_{i=1}^{j-1}\innprdbg{-\innprd{v_j}{e_i}e_i}{e_k} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}+\frac1{c_j}\sum_{i=1}^{j-1}-\innprdbg{v_j}{e_i}\innprdbg{e_i}{e_k} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}-\frac1{c_j}\sum_{i=1}^{j-1}\innprdbg{v_j}{e_i}\innprdbg{e_i}{e_k} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}-\frac1{c_j}\sum_{i=1}^{j-1}\innprdbg{v_j}{e_i}\normalsize{\mathbb{1}_{i=k}} \\ &= \frac1{c_j}\innprdbg{v_j}{e_k}-\frac1{c_j}\innprdbg{v_j}{e_k} \\ &= 0 \end{align*}$$
Let’s see what this looks like.
$$ e_1\equiv\frac{v_1}{\dnorm{v_1}} \quad\quad\quad e_2\equiv\frac{v_2-\innprd{v_2}{e_1}e_1}{\dnorm{v_2-\innprd{v_2}{e_1}e_1}} \quad\quad\quad e_3\equiv\frac{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}{\dnorm{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}} $$
Define $d_j\equiv1/{c_j}$ and note that
$$\begin{align*} e_3 &= \frac{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}{\dnorm{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}} \\ &= \frac1{c_3}\prn{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2} \\ &= d_3\prn{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2} \\ &= d_3v_3-d_3\innprd{v_3}{e_1}e_1-d_3\innprd{v_3}{e_2}e_2 \\ \end{align*}$$
Hence
$$ d_3v_3=d_3\innprd{v_3}{e_1}e_1+d_3\innprd{v_3}{e_2}e_2+e_3 $$
and
$$\begin{align*} v_3 &= \frac1{d_3}\prn{d_3\innprd{v_3}{e_1}e_1+d_3\innprd{v_3}{e_2}e_2+e_3} \\ &= \innprd{v_3}{e_1}e_1+\innprd{v_3}{e_2}e_2+\frac1{d_3}e_3 \\ &= \innprd{v_3}{e_1}e_1+\innprd{v_3}{e_2}e_2+c_3e_3 \end{align*}$$
Hence $v_3\in\text{span}(e_1,e_3,e_3)$.
6.55.i, Properties of orthogonal projection
Let $U$ be a finite-dimensional subspace of $V$ and let $v\in V$. Then 6.47 implies that $V=U\oplus U^\perp$ so that $v=u+w$ for some $u\in U$ and some $w\in U^\perp$. Hence $P_Uv=u$.
Let $e_1,\dots,e_m$ be an orthonormal basis of $U$. Then
$$\begin{align*} P_Uv &= u \\ &= \sum_{k=1}^m\innprd{u}{e_k}e_k\tag{by 6.30} \\ &= \sum_{k=1}^m\innprd{u}{e_k}e_k+\sum_{k=1}^m\innprd{w}{e_k}e_k \\ &= \sum_{k=1}^m\prn{\innprd{u}{e_k}+\innprd{w}{e_k}}e_k \\ &= \sum_{k=1}^m\innprd{u+w}{e_k}e_k \\ &= \sum_{k=1}^m\innprd{v}{e_k}e_k \end{align*}$$
The third equality holds because $w\in U^\perp$. Hence $\innprd{w}{e_k}=0$.
Example 6.58
Let $e_1,e_2,e_3,e_4,e_5,e_6$ be the orthonormal basis given by applying Gram-Schmidt to the basis $1,x,x^2,x^3,x^4,x^5$ of $U$. Hence
$$ e_1\equiv\frac{1}{\dnorm{1}} \quad\quad\quad e_2\equiv\frac{x-\innprd{x}{e_1}e_1}{\dnorm{x-\innprd{x}{e_1}e_1}} \quad\quad\quad e_3\equiv\frac{x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2}{\dnorm{x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2}} $$
$$ e_4\equiv\frac{x^3-\sum_{j=1}^3\innprd{x^3}{e_j}e_j}{\dnorm{x^3-\sum_{j=1}^3\innprd{x^3}{e_j}e_j}} \quad\quad\quad e_5\equiv\frac{x^4-\sum_{j=1}^4\innprd{x^4}{e_j}e_j}{\dnorm{x^4-\sum_{j=1}^4\innprd{x^4}{e_j}e_j}} $$
So we compute
$$ \dnorm{1}=\sqrt{\innprd{1}{1}}=\sqrt{\int_{-\pi}^\pi1(t)\cdot1(t)dt}=\sqrt{t\eval{-\pi}{\pi}}=\sqrt{\pi--\pi}=\sqrt{2\pi} $$
$$ e_1=\frac{1}{\dnorm{1}}=\frac1{\sqrt{2\pi}}1 $$
Next
$$\begin{align*} \innprd{x}{e_1} &= \innprd{x}{\frac1{\sqrt{2\pi}}1} \\ &= \int_{-\pi}^{\pi}x(t)\frac1{\sqrt{2\pi}}1(t)dt \\ &= \frac1{\sqrt{2\pi}}\int_{-\pi}^{\pi}tdt \\ &= \frac1{\sqrt{2\pi}}\frac12\Prn{t^2\eval{-\pi}{\pi}} \\ &= \frac1{\sqrt{2\pi}}\frac12\prn{\pi^2-(-\pi)^2} \\ &= 0 \end{align*}$$
and
$$\begin{align*} \dnorm{x}^2 &= \innprd{x}{x} \\ &= \int_{-\pi}^{\pi}x(t)x(t)dt \\ &= \int_{-\pi}^{\pi}t\cdot tdt \\ &= \int_{-\pi}^{\pi}t^2dt \\ &= \frac13\Prn{t^3\eval{-\pi}{\pi}} \\ &= \frac13\prn{\pi^3-(-\pi)^3} \\ &= \frac13\prn{\pi^3-(-1)^3\pi^3} \\ &= \frac13\prn{\pi^3+\pi^3} \\ &= \frac{2\pi^3}{3} \end{align*}$$
Hence
$$ e_2=\frac{x-\innprd{x}{e_1}e_1}{\dnorm{x-\innprd{x}{e_1}e_1}}=\frac{x}{\dnorm{x}}=\frac{x}{\sqrt{\frac{2\pi^3}{3}}}=\sqrt{\frac{3}{2\pi^3}}x $$
We can compute the other $e_k$’s similarly. Then we can use 6.55(i) to compute the orthogonal projection:
$$\begin{align*} P_Uv &= \sum_{k=1}^6\innprd{v}{e_k}e_k \\ &= \sum_{k=1}^6\innprd{\sin}{e_k}e_k \\ &= \sum_{k=1}^6\Prn{\int_{-\pi}^{\pi}\sin{(t)}e_k(t)dt}e_k \end{align*}$$
Let’s code this up:
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
func_innprd=lambda f,g: integrate.quad(lambda t: f(t)*g(t),-np.pi,np.pi)[0]
func_norm=lambda f: np.sqrt(func_innprd(f,f))
deg=11
orig_bis={}
def orig_basis_vec(i): return lambda t: t**i
for i in range(deg+1): orig_bis[i]=orig_basis_vec(i)
orth_bis={}
ips={}
def compute_inner_prods(k=1):
for i in range(k,deg+1+1):
if i-1 not in orig_bis: continue
xi=orig_bis[i-1]
ek=orth_bis[k]
ips[(i-1,k)]=func_innprd(xi,ek)
return
def gram_schmidt(k=5):
fk=lambda w: orig_bis[k-1](w)-np.sum([ips[(k-1,i)] * orth_bis[i](w) for i in range(1,k)])
nfk=func_norm(fk)
ek=lambda t: (1/nfk) * fk(t)
orth_bis[k]=ek
compute_inner_prods(k=k)
return ek
for i in range(1,deg+1+1): gram_schmidt(k=i)
PUv=lambda v,t,n: np.sum(func_innprd(v,orth_bis[i])*orth_bis[i](t) for i in range(1,n+1))
def graph(funct, x_range, cl='r--', show=False):
y_range=[]
for x in x_range:
y_range.append(funct(x))
plt.plot(x_range,y_range,cl)
return
rs=1.0
r=np.linspace(-rs*np.pi,rs*np.pi,80)
v=lambda t: 15*np.sin(t)*np.power(np.cos(t),3)*np.exp(1/(t-19))
graph(lambda t: PUv(v,t,deg+1),r,cl='r-')
graph(v,r,cl='b--')
plt.axis('equal')
plt.show()
This code produced the following graph. The red line is the polynomial approximation and the blue dashed line is the sine function:
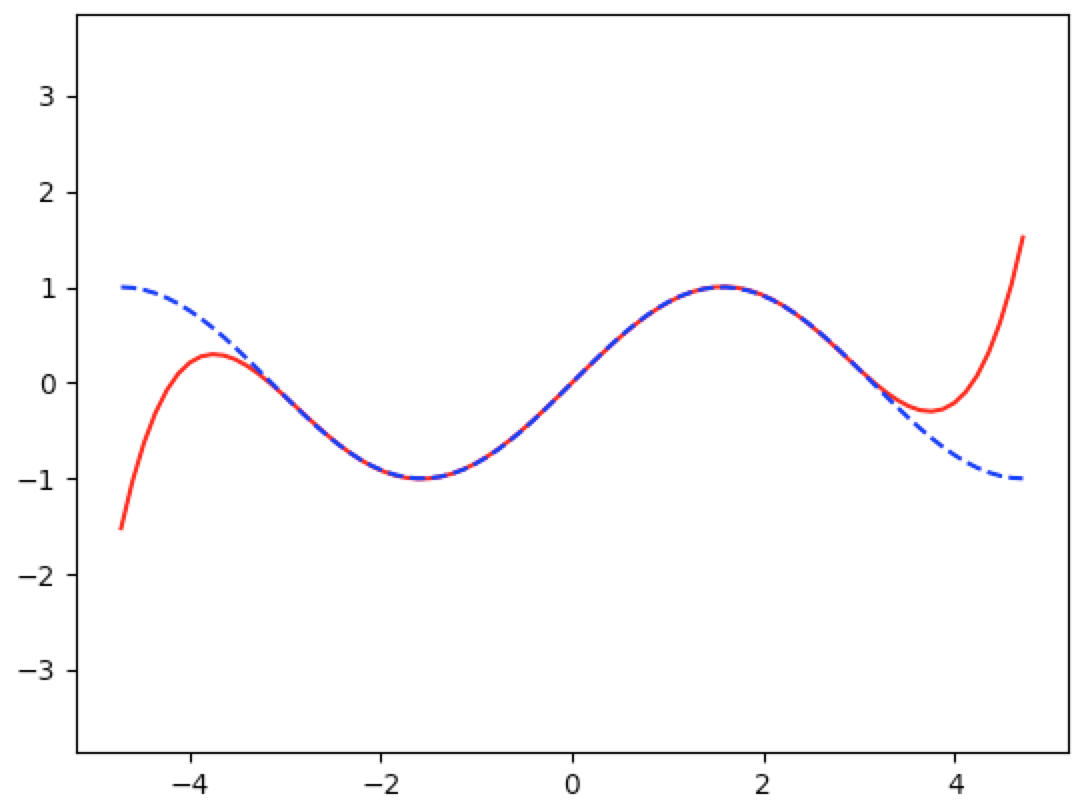
Let’s try this out on a more complicated function:
$$ v(t)\equiv15\cdot\sin{t}\cdot\cos^3{t}\cdot\exp{\Big(\frac1{t-19}\Big)} $$
Using a $5^{th}$ degree polynomial approximation, we get
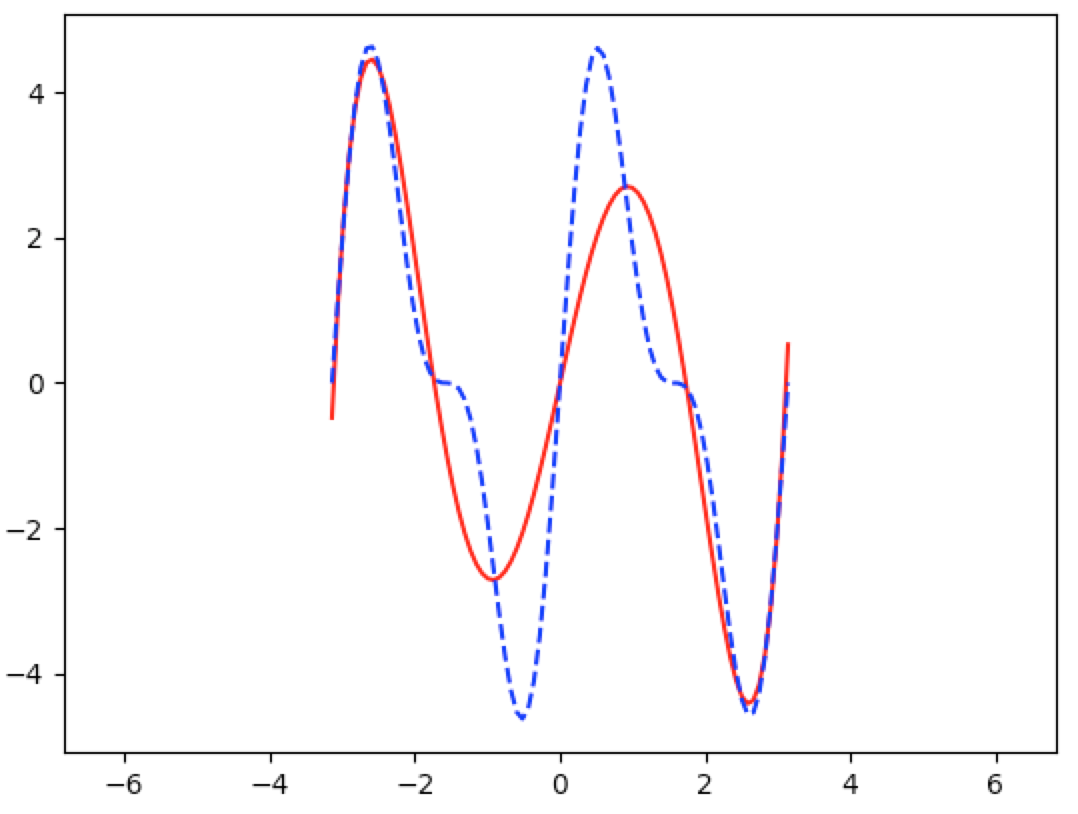
And using an $11^{th}$ degree polynomial approximation, we get
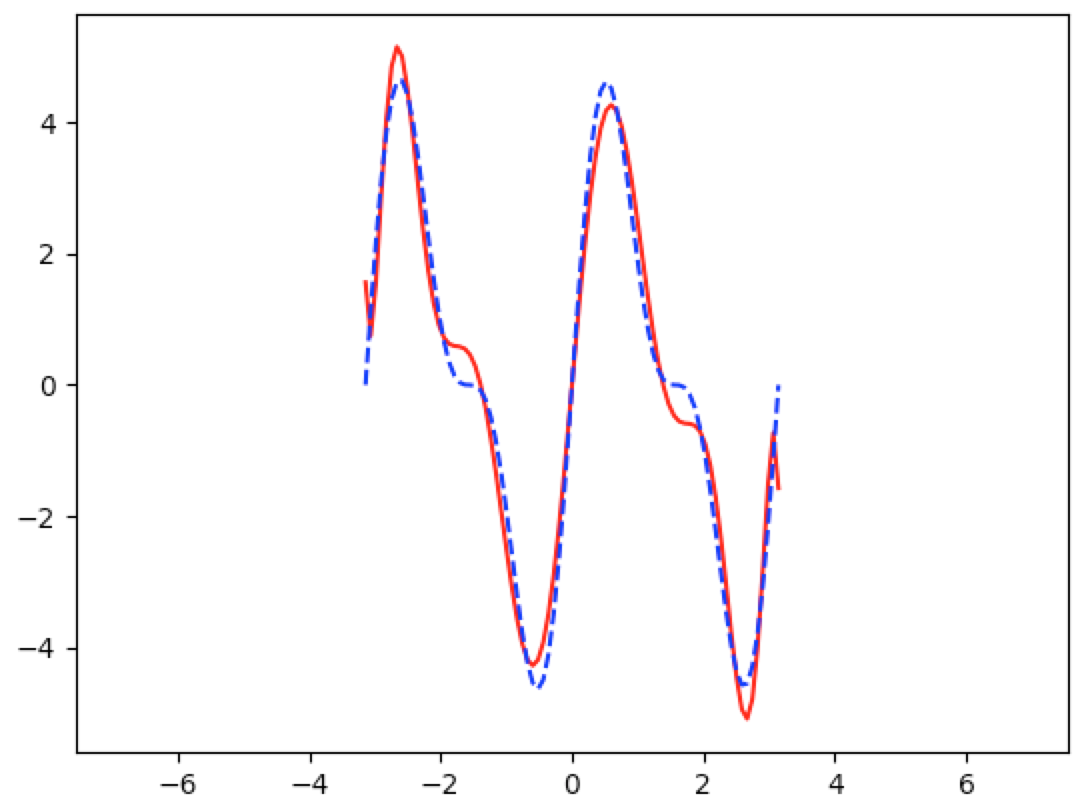
And using a $13^{th}$ degree polynomial approximation, we get
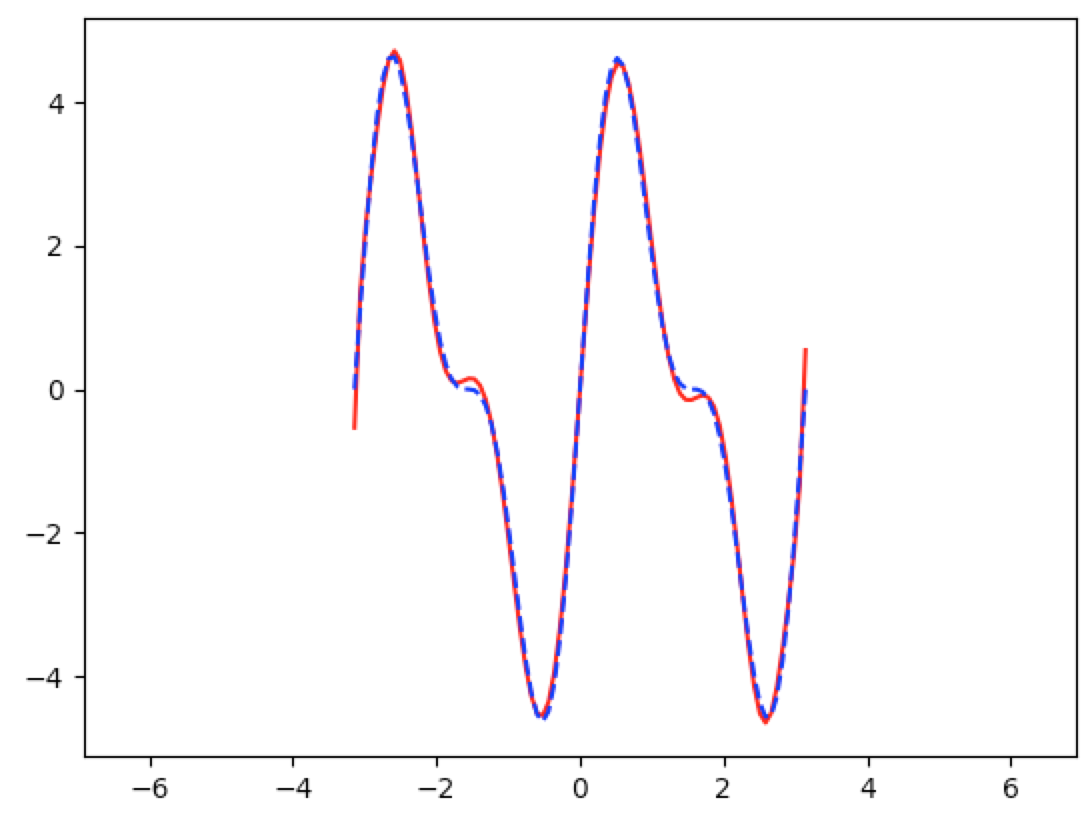
Here is a more concrete but less flexible implementation of the same problem. It’s less flexible because we would have to make substantial changes to increase the degree of the approximation:
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
I=lambda f_x,a,b: integrate.quad(f_x,a,b)[0]
func_mult=lambda f,g,t:f(t)*g(t)
func_innprd=lambda f,g: I(lambda t: func_mult(f,g,t),-np.pi,np.pi)
func_norm=lambda f: np.sqrt(func_innprd(f,f))
x0=lambda t: 1
x1=lambda t: t
x2=lambda t: t**2
x3=lambda t: t**3
x4=lambda t: t**4
x5=lambda t: t**5
nf1=func_norm(x0)
e1=lambda t: (1/nf1) * x0(t)
ip_x1e1=func_innprd(x1,e1)
ip_x2e1=func_innprd(x2,e1)
ip_x3e1=func_innprd(x3,e1)
ip_x4e1=func_innprd(x4,e1)
ip_x5e1=func_innprd(x5,e1)
print("ip_x1e1={} ip_x2e1={} ip_x3e1={} ip_x4e1={} ip_x5e1={}"
.format(ip_x1e1,ip_x2e1,ip_x3e1,ip_x4e1,ip_x5e1))
f2=lambda w: x1(w)-ip_x1e1*e1(w)
nf2=func_norm(f2)
e2=lambda t: (1/nf2) * f2(t)
ip_x2e2=func_innprd(x2,e2)
ip_x3e2=func_innprd(x3,e2)
ip_x4e2=func_innprd(x4,e2)
ip_x5e2=func_innprd(x5,e2)
print("ip_x2e2={} ip_x3e2={} ip_x4e2={} ip_x5e2={}".format(ip_x2e2,ip_x3e2,ip_x4e2,ip_x5e2))
f3=lambda w: x2(w)-(ip_x2e1 * e1(w) + ip_x2e2 * e2(w))
nf3=func_norm(f3)
e3=lambda t: (1/nf3) * f3(t)
ip_x3e3=func_innprd(x3,e3)
ip_x4e3=func_innprd(x4,e3)
ip_x5e3=func_innprd(x5,e3)
print("ip_x3e3={} ip_x4e3={} ip_x5e3={}".format(ip_x3e3,ip_x4e3,ip_x5e3))
f4=lambda w: x3(w)-(ip_x3e1 * e1(w) + ip_x3e2 * e2(w) + ip_x3e3 * e3(w))
nf4=func_norm(f4)
e4=lambda t: (1/nf4) * f4(t)
ip_x4e4=func_innprd(x4,e4)
ip_x5e4=func_innprd(x5,e4)
print("ip_x4e4={} ip_x5e4={}".format(ip_x4e4,ip_x5e4))
f5=lambda w: x4(w)-(ip_x4e1 * e1(w) + ip_x4e2 * e2(w) + ip_x4e3 * e3(w) + ip_x4e4 * e4(w))
nf5=func_norm(f5)
e5=lambda t: (1/nf5) * f5(t)
ip_x5e5=func_innprd(x5,e5)
print("ip_x5e5={}".format(ip_x5e5))
f6=lambda w: x5(w)-(ip_x5e1 * e1(w) + ip_x5e2 * e2(w) + ip_x5e3 * e3(w) + ip_x5e4 * e4(w) + ip_x5e5 * e5(w))
nf6=func_norm(f6)
e6=lambda t: (1/nf6) * f6(t)
orthonormal_basis={1:e1,2:e2,3:e3,4:e4,5:e5,6:e6}
PUv=lambda v,t,n: np.sum(func_innprd(v,orthonormal_basis[i])*orthonormal_basis[i](t) for i in range(1,n+1))
def graph(funct, x_range, cl='r--', show=False):
y_range=[]
for x in x_range:
y_range.append(funct(x))
plt.plot(x_range,y_range,cl)
return
rs=1.0
r=np.linspace(-rs*np.pi,rs*np.pi,100)
v=lambda t: 15*np.sin(t)*np.power(np.cos(t),3)*np.exp(1/(t-19))
graph(lambda t: PUv(v,t,6),r,cl='r-')
graph(v,r,cl='b--')
plt.show()
General
Proposition W.6.G.1 Let $U$ be a finite-dimensional subspace of $V$, let $u_1,\dots,u_n$ be a basis of $U$, and let $v\in V$. Then $v$ is orthogonal to $U$ if and only if $v$ is orthogonal to each of the $u_1,\dots,u_n$.
Proof Suppose $v$ is orthogonal to $U$. Then $v$ is orthogonal to every vector in $U$. Since $u_1,\dots,u_n\in U$, then $v$ is orthogonal to each of them. Conversely, suppose $v$ is orthogonal to each of the $u_1,\dots,u_n$. Let $u=\sum_i^na_iu_i\in U$. Then
$$\begin{align*} \innprd{v}{u}=\innprdBg{v}{\sum_{i=1}^na_iu_i}= \sum_{i=1}^n\innprd{v}{a_iu_i}= \sum_{i=1}^n\overline{a_i}\innprd{v}{u_i}=0\quad\blacksquare \end{align*}$$
Proposition W.6.G.2 Let $U$ be a finite-dimensional subspace of $V$ and let $v\in V$. Then $P_Uv=0$ if and only if $v\in U^\perp$.
Proof Suppose $v\in U^\perp$. Then we can uniquely write $v=0+v$ where $0\in U$ and $v\in U^\perp$ (by 6.47). Hence $P_Uv=0$. Conversely, suppose $P_Uv=0$. Uniquely write $v=u+w$ where $u\in U$ and $w\in U^\perp$ (by 6.47). Then $0=P_Uv=u$. Hence $v=0+w=w\in U^\perp$. $\blacksquare$
Proposition W.6.G.3 Let $U$ be a finite-dimensional subspace of $V$ and let $v\in V$. Then $P_Uv=v$ if and only if $v\in U$.
Proof Suppose $v\in U$. Then we can uniquely write $v=v+0$ where $v\in U$ and $0\in U^\perp$ (by 6.47). Hence $P_Uv=v$. Conversely, suppose $P_Uv=v$. Uniquely write $v=u+w$ where $u\in U$ and $w\in U^\perp$ (by 6.47). Then $v=P_Uv=u\in U$. $\blacksquare$
Example W.6.G.4 Tilt Map Let $e_1,e_2,e_3$ be the standard basis of $\wR^3$ and define $T\in\oper{\wR^3}$ by
$$ Te_1=e_1-e_3 \quad\quad\quad\quad Te_2=e_2 \quad\quad\quad\quad Te_3=0 $$
Then $\rangsp{T}^\perp\neq\nullsp{T}$ but $\dirsum{\rangsp{T}}{\nullsp{T}}=\dirsum{\rangsp{T}}{\rangsp{T}^\perp}=\mathbb{R}^3$.
Also, $T^2=T$ but $\dnorm{Tv}>\dnorm{v}$ for some $v\in\wR^3$ and $T$ is not an orthogonal projection on $\rangsp{T}$.
Note Cross-reference with exercises 6.C.7 and 6.C.8.
Proof Note that $e_1-e_3,e_2$ a basis of $\rangsp{T}$. It’s easy to see this geometrically and it’s simple to show.
Now note that $e_1+e_3=(1,0,1)$ is orthogonal to $e_1-e_3=(1,0,-1)$ and to $e_2=(0,1,0)$. Hence $e_1+e_3\in\rangsp{T}^\perp$. But
$$ T(e_1+e_3)=Te_1+Te_3=e_1-e_3+0=(1,0,-1)\neq(0,0,0) $$
Hence $e_1+e_3\notin\nullsp{T}$ and $\rangsp{T}^\perp\not\subset\nullsp{T}$. Hence $\rangsp{T}^\perp\neq\nullsp{T}$.
Furthermore, note that $e_3\in\nullsp{T}$. But $e_3\notin\rangsp{T}^\perp$ since
$$ \innprd{e_3}{e_1-e_3}=\innprd{e_3}{e_1}-\innprd{e_3}{e_3}=0-1=-1 $$
Hence $\nullsp{T}\not\subset\rangsp{T}^\perp$.
Let $w\in\mathbb{R}^3$ with $w=ae_1+be_2+ce_3$. Then
$$\align{ w &= ae_1+be_2+ce_3 \\ &= ae_1+be_2+ce_3-ae_3+ae_3 \\ &= ae_1-ae_3+be_2+ce_3+ae_3 \\ &= a(e_1-e_3)+be_2+(c+a)e_3 \\ &\in\rangsp{T}+\nullsp{T} }$$
where the inclusion holds because $a(e_1-e_3)+be_2\in\rangsp{T}$ and $(c+a)e_3\in\nullsp{T}$. Hence $\mathbb{R}^3=\rangsp{T}+\nullsp{T}$. Also, let $v\in\rangsp{T}\cap\nullsp{T}$. Then $v=a(e_1-e_3)+be_2$ and $v=ce_3$ and
$$\align{ ce_3 &= v \\ &= a(e_1-e_3)+be_2 \\ &= ae_1-ae_3+be_2 \\ &= ae_1+be_2-ae_3 }$$
or
$$\align{ 0 &= ae_1+be_2-ae_3-ce_3 \\ &= ae_1+be_2+(-a-c)e_3 \\ }$$
Then the linear independence of $e_1,e_2,e_3$ implies that $0=a=b$. Hence $v=a(e_1-e_3)+be_2=0$ and $\mathbb{R}^3=\dirsum{\rangsp{T}}{\nullsp{T}}$.
Again let $w\in\mathbb{R}^3$ with $w=ae_1+be_2+ce_3$. Then define $r\equiv\frac{a-c}2$ and $t\equiv\frac{a+c}2$. Then
$$ r+t=\frac{a-c}2+\frac{a+c}2=\frac{a-c+a+c}2=\frac{2a}2=a $$
and
$$ t-r=\frac{a+c}2-\frac{a-c}2=\frac{a+c-(a-c)}2=\frac{a+c-a+c}2=\frac{2c}2=c $$
and
$$\align{ w &= ae_1+be_2+ce_3 \\ &= (r+t)e_1+be_2+(t-r)e_3 \\ &= re_1+te_1+be_2+te_3-re_3 \\ &= re_1-re_3+be_2+te_1+te_3 \\ &= r(e_1-e_3)+be_2+t(e_1+e_3) \\ &\in\rangsp{T}+\rangsp{T}^\perp }$$
where the inclusion holds because $r(e_1-e_3)+be_2\in\rangsp{T}$ and $t(e_1+e_3)\in\rangsp{T}^\perp$. Hence $\mathbb{R}^3=\rangsp{T}+\rangsp{T}^\perp$. Also, let $v\in\rangsp{T}\cap\rangsp{T}^\perp$. Then $v=a(e_1-e_3)+be_2$ and $v=c(e_1+e_3)$ and
$$\align{ ce_1+ce_3 &= c(e_1+e_3) \\ &= v \\ &= a(e_1-e_3)+be_2 \\ &= ae_1-ae_3+be_2 \\ &= ae_1+be_2-ae_3 }$$
or
$$\align{ 0 &= ae_1-ce_1+be_2-ae_3-ce_3 \\ &= (a-c)e_1+be_2+(-a-c)e_3 \\ &= (a-c)e_1+be_2+(-1)(a+c)e_3 \\ }$$
Then the linear independence of $e_1,e_2,e_3$ implies that
$$\align{ a-c=0=a+c &\iff -c=c \\ &\iff c=0 }$$
Hence $v=c(e_1+e_3)=0$ and $\mathbb{R}^3=\dirsum{\rangsp{T}}{\rangsp{T}^\perp}$.
Note that $T=T^2$ since
$$\align{ T^2e_1 &= T(Te_1)=T(e_1-e_3)=Te_1-Te_3=e_1-e_3-0=Te_1 \\ T^2e_2 &= T(Te_2)=Te_2 \\ T^2e_3 &= T(Te_3)=T(0)=0=Te_3 }$$
Next, define $v\in\wR^3$ as $v=ae_1+be_2+ce_3$ for $a,b,c\in\wR$ where $\norm{c}<\norm{a}$. Then
$$\align{ \dnorm{Tv}^2 &= \dnorm{aTe_1+bTe_2+cTe_3}^2 \\ &= \dnorm{a(e_1-e_3)+be_2}^2 \\ &= \dnorm{ae_1+be_2-ae_3}^2 \\ &= \norm{a}^2+\norm{b}^2+\norm{-a}^2\tag{by 6.25} \\ &= \norm{a}^2+\norm{b}^2+\norm{a}^2 \\ &> \norm{a}^2+\norm{b}^2+\norm{c}^2 \\ &= \dnorm{ae_1+be_2+ce_3}^2\tag{by 6.25} \\ &= \dnorm{v}^2 }$$
And $T$ is not an orthogonal projection on $\rangsp{T}$. We can prove this in a few ways. First, if $T$ was an orthogonal projection on $\rangsp{T}$, then it must be that $\nullsp{T}=\rangsp{T}^\perp$ (by 6.55(e)). But we already proved that that’s not the case. Similarly, if $T$ was an orthogonal projection, then it must be that $\dnorm{Tv}\leq\dnorm{v}$ for all $v\in\wR^3$ (by 6.55(h)). Again we proved that that’s not the case. We can also prove this directly. Let $v\in\wR^3$ so that $v=u+w$ for some $u\in\rangsp{T}$ and some $w\in\rangsp{T}^\perp$. Then
$$ u=a(e_1-e_3)+be_2 \quad\quad\quad\quad w=c(e_1+e_3) $$
and
$$\align{ Tv &= T(u+w) \\ &= Tu+Tw \\ &= T\prn{a(e_1-e_3)+be_2}+T\prn{c(e_1+e_3)} \\ &= T(ae_1-ae_3+be_2)+T(ce_1+ce_3) \\ &= aTe_1-aTe_3+bTe_2+cTe_1+cTe_3 \\ &= aTe_1+cTe_1+bTe_2+cTe_3-aTe_3 \\ &= (a+c)Te_1+bTe_2+(c-a)Te_3 \\ &= (a+c)(e_1-e_3)+be_2 \\ }$$
Hence $Tv$ doesn’t generally equal $u$ (unless $c=0$). $\blacksquare$
Motivation W.6.G.5 let $e_1,\dots,e_n$ be an orthonormal basis of $V$. Define
$$ \varphi(e_k)\equiv1\quad\text{for }k=1,\dots,m $$
Then there exists a unique $u_1\in V$ such that $\varphi(v)=\innprd{v}{u_1}_1$. And there exists a unique $u_2\in V$ such that $\varphi(v)=\innprd{v}{u_2}_2$. Then
$$\align{ \innprd{v}{w}_1 &= \innprdBg{\sum_{k=1}^n\innprd{v}{e_k}_1e_k}{w}_1 \\ &= \sum_{k=1}^n\innprdbg{\innprd{v}{e_k}_1e_k}{w}_1 \\ &= \sum_{k=1}^n\innprd{v}{e_k}_1\innprd{e_k}{w}_1 \\ &= \sum_{k=1}^n\innprd{v}{e_k}_1\innprdBg{e_k}{\sum_{j=1}^n\innprd{w}{e_j}_1e_j}_1 \\ &= \sum_{k=1}^n\innprd{v}{e_k}_1\sum_{j=1}^n\innprdbg{e_k}{\innprd{w}{e_j}_1e_j}_1 \\ &= \sum_{k=1}^n\innprd{v}{e_k}_1\sum_{j=1}^n\overline{\innprd{w}{e_j}_1}\innprd{e_k}{e_j}_1 \\ &= \sum_{k=1}^n\sum_{j=1}^n\innprd{v}{e_k}_1\overline{\innprd{w}{e_j}_1}\mathbb{1}_{k=j} \\ &= \sum_{k=1}^n\innprd{v}{e_k}_1\overline{\innprd{w}{e_k}_1} \\ }$$
Proposition W.6.G.6 Let $V$ be a real inner product space such that $\dim{V}=1$. Then there are exactly two vectors in $V$ with norm $1$.
Proof Pick any nonzero vector $v\in V$. Then $v$ is a basis of $V$. We want to count the number of unit-norm vectors $e$ in $V$. Note that any such $e$ must satisfy $e=cv$ for some constant $c$. We will first show that $c$ must be one of two possible values.
Suppose $f$ is a unit-norm vector with $f=cv$. Then
$$ 1=\dnorm{f}=\dnorm{cv}=\normw{c}\dnorm{v} $$
Solving for $c$, we see that
$$ \normw{c}=\frac1{\dnorm{v}} $$
or
$$ c=\pm\frac1{\dnorm{v}} $$
Hence if $e$ is a unit-norm vector in $V$, then
$$ e=\pm\frac1{\dnorm{v}}v $$
That is, there are exactly two unit-norm vectors in $V$. $\blacksquare$
Proposition W.6.G.7 Let $W$ be inner product space and let $T\in\linmap{V}{W}$. Then $T=0$ if and only if $Tv$ is orthogonal to $w$ for every $v\in V$ and every $w\in W$.
Proof First suppose that $Tv$ is orthogonal to $w$ for every $v\in V$ and every $w\in W$. Let $u\in V$. Then $0=\innprd{Tu}{w}$ for every $w\in W$. In particular $0=\innprd{Tu}{Tu}$. Then the definiteness of an inner product implies that $0=Tu$.
Conversely, if $T=0$, then $Tv=0$ for every $v\in V$ and hence $Tv$ is orthogonal to $w$ for every $v\in V$ and every $w\in W$. $\blacksquare$
Proposition W.6.G.8 Let $W$ be inner product space. Then $T\in\linmap{V}{W}$ is uniquely determined by the values of $\innprd{Tv}{w}$ for all $v\in V$ and all $w\in W$.
Proof Suppose another map $S\in\linmap{V}{W}$ satisfies
$$ \innprd{Sv}{w}=\innprd{Tv}{w} $$
for all $v\in V$ and all $w\in W$. Hence
$$ 0=\innprd{Sv}{w}-\innprd{Tv}{w}=\innprd{Sv-Tv}{w}=\innprd{(S-T)v}{w} $$
for all $v\in V$ and all $w\in W$. Hence $(S-T)v$ is orthogonal to $w$ for all $v\in V$ and all $w\in W$. Then proposition W.6.G.7 implies that $S-T=0$. $\blacksquare$
Proposition W.6.G.9 On the vector space $\wC^n$, define $\innprd{\cdot}{\cdot}_{\wC^n}$ by
$$ \innprd{w}{z}_{\wC^n}\equiv\sum_{k=1}^nw_k\cj{z_k} $$
for $w=(w_1,\dots,w_n)\in\wC^n$ and $z=(z_1,\dots,z_n)\in\wC^n$. Then $\innprd{\cdot}{\cdot}_{\wC^n}$ satisfies the properties of an inner product.
Proof Positivity:
$$ \innprd{z}{z}_{\wC^n}=\sum_{k=1}^nz_k\cj{z_k}=\sum_{k=1}^n\norm{z}^2\geq0 $$
The second equality follows from 4.5.product of $z$ and $\cj{z}$.
Definiteness: First suppose that $z=0$ so that $z=(0,\dots,0)$. Then
$$ \innprd{z}{z}_{\wC^n}=\sum_{k=1}^n0\cj{0}=\sum_{k=1}^n0=0 $$
Now suppose that $0=\innprd{z}{z}_{\wC^n}$. Then
$$ 0=\innprd{z}{z}_{\wC^n}=\sum_{k=1}^nz_k\cj{z_k}=\sum_{k=1}^n\norm{z_k}^2 $$
Proposition W.4.4 gives that $\norm{z_k}^2\geq0$ for $k=1,\dots,n$. Hence if $\norm{z_k}^2>0$ for some $k$, then the above equality fails because there are no negative numbers in the sum to offset any positive numbers in the sum. Hence $\norm{z_k}^2=0$ for $k=1,\dots,n$. Then proposition W.4.5 implies that $z_k=0$ for $k=1,\dots,m$. Hence $z=0$.
Additivity in the first slot:
$$ \innprd{w+x}{z}_{\wC^n}=\sum_{k=1}^n(w_k+x_k)\cj{z_k}=\sum_{k=1}^n(w_k\cj{z_k}+x_k\cj{z_k})=\sum_{k=1}^nw_k\cj{z_k}+\sum_{k=1}^nx_k\cj{z_k}=\innprd{w}{z}_{\wC^n}+\innprd{x}{z}_{\wC^n} $$
Homogeneity in the first slot:
$$ \innprd{\lambda w}{z}_{\wC^n}=\innprd{(\lambda w_1,\dots,\lambda w_n)}{z}_{\wC^n}=\sum_{k=1}^n(\lambda w_k)\cj{z_k}=\lambda\sum_{k=1}^nw_k\cj{z_k}=\lambda\innprd{w}{z}_{\wC^n} $$
Conjugate symmetry:
$$ \innprd{w}{z}_{\wC^n}=\sum_{k=1}^nw_k\cj{z_k}=\sum_{k=1}^n\cj{z_k\cj{w_k}}=\cj{\sum_{k=1}^nz_k\cj{w_k}}=\cj{\innprd{z}{w}_{\wC^n}} $$
The second equality is given by W.4.3 and the third equality is given by 4.5.additivity. $\wes$
Proposition W.6.G.10 Let $V$ be an inner product space. If $S,T\in\oper{V}$ satisfy $\innprd{Su}{v}=\innprd{Tu}{v}$ for all $u,v\in V$, then $S=T$.
Proof This follows from W.6.G.8 with $W\equiv V$. $\wes$
Connection W.6.G.11 Let $T\in\linmap{\wR^2}{\wR^3}$ and let $A=\mtrxof{T}$. For any $x\in\wR^2$ and any $w\in\wR^3$, we have
$$ \innprd{Tx}{w}=\innprd{x}{T^*w} $$
$$ Ax\cdot w = (Ax)^tw = x^tA^tw = x\cdot A^tw $$
and
$$ \innprd{x}{T^*Tx}=\innprd{Tx}{Tx} $$
$$ x\cdot A^tAx=x^t(A^tAx)=(x^tA^t)Ax=(Ax)^tAx=Ax\cdot Ax $$
$\wes$
Proposition W.6.G.12 Let $z_1,\dots,z_n\in\wC^n$. Then $z_1,\dots,z_n$ is orthonormal if and only if $\cj{z_1},\dots,\cj{z_n}$ is orthonormal (with respect to $\innprd{\cdot}{\cdot}_{\wC^n}$ from W.6.G.9).
Proof Suppose $z_1,\dots,z_n$ is orthonormal. Then
$$ \innprd{\cj{z_j}}{\cj{z_k}}=\sum_{i=1}^n\cj{z_{i,j}}\;\cj{\cj{z_{i,k}}}=\sum_{i=1}^n\cj{z_{i,j}}z_{i,k}=\sum_{i=1}^nz_{i,k}\cj{z_{i,j}}=\innprd{z_k}{z_j}=\cases{1&j=k\\0&j\neq k} $$
Suppose $\cj{z_1},\dots,\cj{z_n}$ is orthonormal. Then
$$ \innprd{z_k}{z_j}=\sum_{i=1}^nz_{i,k}\cj{z_{i,j}}=\sum_{i=1}^n\cj{z_{i,j}}z_{i,k}=\sum_{i=1}^n\cj{z_{i,j}}\;\cj{\cj{z_{i,k}}}=\innprd{\cj{z_j}}{\cj{z_k}}=\cases{1&j=k\\0&j\neq k} $$
$\wes$
Proposition W.6.G.13 Let $w,z\in\wC^n$. Then
$$ \innprd{\cj{w}}{z}=\innprd{\cj{z}}{w} $$
Proof We have
$$ \innprd{\cj{w}}{z}=\sum_{j=1}^n\cj{w_j}\;\cj{z_j}=\sum_{j=1}^n\cj{z_j}\;\cj{w_j}=\innprd{\cj{z}}{w} $$
$\wes$
Counterexample W.6.G.14 Let $z_1,z_2,\dots,z_n\in\wC^n$ be orthonormal with respect to $\innprddt_{\wC^n}$ (from W.6.G.9). It’s NOT necessarily true that $0=\innprd{\cj{z_j}}{z_k}$ for $j\neq k$. NOR is it necessarily true that $1=\innprd{\cj{z_j}}{z_j}$.
For example, define $z_1\equiv\frac{(i,1)}{\sqrt2}$ and $z_2\equiv\frac{(-i,1)}{\sqrt2}$. Then $z_1,z_2$ is orthonormal in $\wC^2$:
$$\align{ \innprd{z_1}{z_2} &= \innprdBg{\frac{(i,1)}{\sqrt2}}{\frac{(-i,1)}{\sqrt2}} \\ &= \frac1{\sqrt2}\frac1{\sqrt2}\innprdbg{(i,1)}{(-i,1)} \\ &= \frac12(i\cdot\cj{(-i)}+1\cdot\cj{1})\tag{by W.6.G.9} \\ &= \frac12(i\cdot i+1) \\ &= \frac12(-1+1) \\ &= 0 }$$
$$\align{ \innprd{z_1}{z_1} &= \innprdBg{\frac{(i,1)}{\sqrt2}}{\frac{(i,1)}{\sqrt2}} \\ &= \frac1{\sqrt2}\frac1{\sqrt2}\innprdbg{(i,1)}{(i,1)} \\ &= \frac12(i\cdot\cj{i}+1\cdot\cj{1})\tag{by W.6.G.9} \\ &= \frac12(i\cdot(-i)+1) \\ &= \frac12(-i^2+1) \\ &= \frac12(-(-1)+1) \\ &= \frac12(1+1) \\ &= 1 }$$
$$\align{ \innprd{z_2}{z_2} &= \innprdBg{\frac{(-i,1)}{\sqrt2}}{\frac{(-i,1)}{\sqrt2}} \\ &= \frac1{\sqrt2}\frac1{\sqrt2}\innprdbg{(-i,1)}{(-i,1)} \\ &= \frac12(-i\cdot\cj{-i}+1\cdot\cj{1})\tag{by W.6.G.9} \\ &= \frac12(-i\cdot i+1) \\ &= \frac12(-i^2+1) \\ &= \frac12(-(-1)+1) \\ &= \frac12(1+1) \\ &= 1 }$$
Note that
$$\align{ \cj{z_1} &= \cj{\Prn{\frac{(i,1)}{\sqrt2}}} \\ &= \cj{\Prn{\frac{i}{\sqrt2},\frac{1}{\sqrt2}}} \\ &= \Prngg{\cj{\Prn{\frac{i}{\sqrt2}}},\cj{\Prn{\frac{1}{\sqrt2}}}} \\ &= \Prngg{\cj{\Prn{\frac{1}{\sqrt2}}}\;\cj{i},\frac{1}{\sqrt2}} \\ &= \Prngg{\frac{1}{\sqrt2}(-i),\frac{1}{\sqrt2}} \\ &= \frac1{\sqrt2}(-i,1) \\ &= z_2 }$$
Hence $\innprd{\cj{z_1}}{z_2}=\innprd{z_2}{z_2}=1\neq0$. Or
$$\align{ \innprd{\cj{z_1}}{z_2} &= \innprdBgg{\frac1{\sqrt2}(-i,1)}{\frac{(-i,1)}{\sqrt2}} \\ &= \frac1{\sqrt2}\frac1{\sqrt2}\innprdbg{(-i,1)}{(-i,1)} \\ &= \frac12(-i\cdot\cj{(-i)}+1\cdot\cj{1})\tag{by W.6.G.9} \\ &= \frac12(-i\cdot i+1) \\ &= \frac12(-i^2+1) \\ &= \frac12(-(-1)+1) \\ &= \frac12(1+1) \\ &\neq 0 }$$
Hence $\innprd{\cj{z_1}}{z_1}=\innprd{z_2}{z_1}=0\neq1$. Or
$$\align{ \innprd{\cj{z_1}}{z_1} &= \innprdBgg{\frac1{\sqrt2}(-i,1)}{\frac{(i,1)}{\sqrt2}} \\ &= \frac1{\sqrt2}\frac1{\sqrt2}\innprdbg{(-i,1)}{(i,1)} \\ &= \frac12(-i\cdot\cj{(i)}+1\cdot\cj{1})\tag{by W.6.G.9} \\ &= \frac12(-i\cdot(-i)+1) \\ &= \frac12(i^2+1) \\ &= \frac12(-1+1) \\ &\neq 1 }$$
Similarly
$$\align{ \cj{z_2} &= \cj{\Prn{\frac{(-i,1)}{\sqrt2}}} \\ &= \cj{\Prn{\frac{-i}{\sqrt2},\frac{1}{\sqrt2}}} \\ &= \Prngg{\cj{\Prn{\frac{-i}{\sqrt2}}},\cj{\Prn{\frac{1}{\sqrt2}}}} \\ &= \Prngg{\cj{\Prn{\frac{1}{\sqrt2}}}\;\cj{(-i)},\frac{1}{\sqrt2}} \\ &= \Prngg{\frac{1}{\sqrt2}i,\frac{1}{\sqrt2}} \\ &= \frac1{\sqrt2}(i,1) \\ &= z_1 }$$
Hence $\innprd{\cj{z_2}}{z_1}=\innprd{z_1}{z_1}=1\neq0$ and $\innprd{\cj{z_2}}{z_2}=\innprd{z_1}{z_2}=0\neq1$. $\wes$
Example W.6.G.15 Define
$$ w\equiv\pmtrx{w_1\\w_2}\in\wC^2 \dq\dq z\equiv\pmtrx{z_1\\z_2}\in\wC^2 $$
Then
$$\align{ \pmtrx{\adjt{w}\\\adjt{z}}z &= \pmtrx{\cj{w_1}&\cj{w_2}\\\cj{z_1}&\cj{z_2}}\pmtrx{z_1\\z_2} \\\\ &= \pmtrx{\cj{w_1}z_1+\cj{w_2}z_2\\\cj{z_1}z_1+\cj{z_2}z_2} \\\\ &= \pmtrx{z_1\cj{w_1}+z_2\cj{w_2}\\z_1\cj{z_1}+z_2\cj{z_2}} \\\\ &= \pmtrx{\innprd{z}{w}_{\wC^2}\\\innprd{z}{z}_{\wC^2}} }$$
Proposition W.6.G.17 Suppose $v_1,\dots,v_n$ is an orthogonal list - each vector is orthogonal to all the other vectors in the list. Let $e_1,\dots,e_n$ be the result of applying Gram-Schmidt to $v_1,\dots,v_n$. Then
$$ e_j = \frac{v_j}{\dnorm{v_j}} $$
for $j=1,\dots,n$.
Proof By definition, $e_1\equiv v_1\big/\dnorm{v_1}$. And since
$$ \innprd{v_2}{e_1} = \innprdBg{v_2}{\frac{v_1}{\dnorm{v_1}}} = \cj{\Prn{\frac1{\dnorm{v_1}}}}\innprd{v_2}{v_1}=0 $$
then
$$ e_2 = \frac{v_2-\innprd{v_2}{e_1}e_1}{\dnorm{v_2-\innprd{v_2}{e_1}e_1}} = \frac{v_2}{\dnorm{v_2}} $$
Let $j\in{3,\dots,n}$. Our induction assumption is that $e_k=v_k\big/\dnorm{v_k}$ for any $k=1,\dots,j-1$. Hence, for any $k=1,\dots,j-1$, we have
$$ \innprd{v_j}{e_k} = \innprdBg{v_j}{\frac{v_k}{\dnorm{v_k}}} = \cj{\Prn{\frac1{\dnorm{v_k}}}}\innprd{v_j}{v_k}=0 $$
Hence
$$ e_j = \frac{v_j-\sum_{k=1}^{j-1}\innprd{v_j}{e_k}e_k}{\dnorm{v_j-\sum_{k=1}^{j-1}\innprd{v_j}{e_k}e_k}} = \frac{v_j}{\dnorm{v_j}} $$
$\wes$
Proposition W.6.G.18 Let $T\wiov$. Then $T=I$ if and only if $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$.
Proof First suppose that $T=I$. Then, for all $u,v\in V$, we have
$$ \innprd{Tu}{v}=\innprd{Iu}{v}=\innprd{u}{v} $$
Conversely, suppose that $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$. Fix $u\in V$. Then, for all $v\in V$, we have
$$ \innprd{Iu}{v}=\innprd{u}{v}=\innprd{Tu}{v} $$
Hence, for all $v\in V$, we have
$$ 0=\innprd{Tu}{v}-\innprd{Iu}{v}=\innprd{Tu-Iu}{v} $$
In particular, put $v\equiv Tu-Iu$. Then
$$ 0=\innprd{Tu-Iu}{Tu-Iu} $$
By the definiteness of an inner product, we get $Tu-Iu=0$. Since $u$ was chosen arbitrarility, then $Tu-Iu=0$ all of $u\in V$. $\wes$
Proposition W.6.G.19 Let $T\wiov$ and let $e_1,\dots,e_n$ be a basis of $V$. Then $T=I$ if and only if $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$.
Proof By the previous proposition, it suffices to show that $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$ if and only if $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$.
First suppose that $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$. Then $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$.
Conversely, suppose that $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$. Then
$$ \innprd{Tu}{v}=\innprdBg{T\Prn{\sum_{j=1}^nu_je_j}}{\sum_{k=1}^nv_ke_k}=\innprdBg{\sum_{j=1}^nu_jTe_j}{\sum_{k=1}^nv_ke_k}=\sum_{j=1}^n\sum_{k=1}^nu_i\cj{v_i}\innprd{Te_j}{e_k}=\sum_{j=1}^n\sum_{k=1}^nu_i\cj{v_i}\innprd{e_j}{e_k}=\innprd{u}{v} $$
$\wes$