Exercises 6.A
(1) Show that the function that takes $\prn{(x_1,x_2),(y_1,y_2)}\in\mathbb{R}^2\times\mathbb{R}^2$ to $\norm{x_1y_1}+\norm{x_2y_2}$ is not an inner product on $\mathbb{R}^2$.
Solution Define
$$ \phi\prn{(x_1,x_2),(y_1,y_2)}\equiv\norm{x_1y_1}+\norm{x_2y_2} $$
And define $u\equiv(x_1,x_2)$ and $v\equiv(y_1,y_2)$ for $x_1,x_2,y_1,y_2\in\mathbb{R}$ such that $\norm{x_1y_1}+\norm{x_2y_2}>0$.
$$\begin{align*} \phi(-4u,v) &= \phi\prn{-4(x_1,x_2),(y_1,y_2)} \\ &= \phi\prn{(-4x_1,-4x_2),(y_1,y_2)} \\ &= \norm{-4x_1y_1}+\norm{-4x_2y_2} \\ &= 4\norm{x_1y_1}+4\norm{x_2y_2} \\ &= 4\prn{\norm{x_1y_1}+\norm{x_2y_2}} \\ &\neq -4\prn{\norm{x_1y_1}+\norm{x_2y_2}} \\ &= -4\phi\prn{(x_1,x_2),(y_1,y_2)} \\ &= -4\phi(u,v) \\ \end{align*}$$
Hence the property of homogeneity in the first slot is not satisied by $\phi$. $\blacksquare$
(2) Show that the function that takes $\prn{(x_1,x_2,x_3),(y_1,y_2,y_3)}\in\mathbb{R}^3\times\mathbb{R}^3$ to $x_1y_1+x_3y_3$ is not an inner product on $\mathbb{R}^3$.
Solution Define
$$ \phi\prn{(x_1,x_2,x_3),(y_1,y_2,y_3)}\equiv x_1y_1+x_3y_3 $$
Then
$$ \phi\prn{(0,1,0),(0,1,0)}=0\cdot0+0\cdot0=0 $$
But $\prn{(0,1,0),(0,1,0)}\neq\prn{(0,0,0),(0,0,0)}=0\in\mathbb{R}^3\times\mathbb{R}^3$. Hence the definiteness property of inner products is not satisfied. $\blacksquare$
(3) Suppose $\mathbb{F}=\mathbb{R}$ and $V\neq\{0\}$. Replace the positivity condition (which states that $\innprd{v}{v}\geq0$ for all $v\in V$) in the definition of an inner product (6.3) with the condition that $\innprd{v}{v}>0$ for some $v\in V$. Show that this change in the definition does not change the set of functions from $V\times V$ to $\mathbb{R}$ that are inner products on $V$.
Proof Let $W$ denote the set of functions from $V\times V$ to $\mathbb{R}$ that are inner products. And let $X$ denote the set of functions from $V\times V$ to $\mathbb{R}$ that satisy the modified inner product properties.
Let $\innprd{\cdot}{\cdot}\in W$. Then $\innprd{v}{v}\geq0$ for all $v\in V$. Since $V\neq\{0\}$, then there exists $a\in V$ such that $a\neq0$. Then the definiteness of $\innprd{\cdot}{\cdot}$ gives $\innprd{a}{a}\neq0$. Then positivity gives $\innprd{a}{a}>0$. Hence $\innprd{\cdot}{\cdot}\in X$ and $W\subset X$.
In the other direction, let $\innprd{\cdot}{\cdot}\in X$. Then there exists $v\in V$ such that $\innprd{v}{v}>0$. Let $u\in V$. We want to show that $\innprd{u}{u}\geq0$.
First suppose that $u$ is a linear combination of $v$. There exists $\lambda\in\mathbb{R}$ such that $u=\lambda v$ and
$$\begin{align*} \innprd{u}{u} &= \innprd{\lambda v}{\lambda v} \\ &= \lambda\innprd{v}{\lambda v}&\quad &\text{first slot homogeneity} \\ &= \lambda\overline{\innprd{\lambda v}{v}}&\quad &\text{conjugate symmetry} \\ &= \lambda\innprd{\lambda v}{v}&\quad &\mathbb{F}=\mathbb{R} \\ &= \lambda^2\innprd{v}{v}&\quad &\text{first slot homogeneity} \\ &\geq 0 &\quad &\lambda^2\geq0\text{ and }\innprd{v}{v}>0 \end{align*}$$
Now suppose $u$ is not a linear combination of $v$. That is, there exists no $\lambda\in\mathbb{R}$ such that $v+\lambda u=0$. Then the definiteness property of inner products gives
$$ 0\neq\innprd{v+\lambda u}{v+\lambda u}\quad\text{for all }\lambda\in\mathbb{R} \tag{6.A.3} $$
By way of contradiction, suppose $\innprd{u}{u}<0$. Then
$$\begin{align*} \innprd{v+\lambda u}{v+\lambda u} &= \innprd{v}{v+\lambda u}+\innprd{\lambda u}{v+\lambda u} \\ &= \innprd{v}{v}+\innprd{v}{\lambda u}+\innprd{\lambda u}{v}+\innprd{\lambda u}{\lambda u} \\ &= \innprd{v}{v}+\lambda\innprd{v}{u}+\lambda\innprd{u}{v}+\lambda^2\innprd{u}{u} \\ &= \innprd{v}{v}+\lambda\innprd{v}{u}+\lambda\innprd{v}{u}+\lambda^2\innprd{u}{u} \\ &= \innprd{v}{v}+2\lambda\innprd{v}{u}+\lambda^2\innprd{u}{u} \\ \end{align*}$$
This is a second-degree polynomial in $\lambda$ with coefficients $a=\innprd{u}{u}$, $b=2\innprd{v}{u}$, and $c=\innprd{v}{v}$. Setting this polynomial to zero, we can use the quadratic formula to solve for $\lambda$:
$$ \lambda=\frac{-2\innprd{v}{u}\pm\sqrt{\prn{2\innprd{v}{u}}^2-4\innprd{u}{u}\innprd{v}{v}}}{2\innprd{u}{u}} $$
Note that $c=\innprd{v}{v}>0$. And the contradiction assumption gives $a=\innprd{u}{u}<0$. Hence
$$ \prn{2\innprd{v}{u}}^2-4\innprd{u}{u}\innprd{v}{v}>0 $$
Hence there exists $\lambda\in\mathbb{R}$ such that
$$ 0=\innprd{v}{v}+2\lambda\innprd{v}{u}+\lambda^2\innprd{u}{u}=\innprd{v+\lambda u}{v+\lambda u} $$
But this contradicts 6.A.3. Hence $\innprd{u}{u}\geq0$. Since $u\in V$ was arbitrarily chosen, then the positivity of $\innprd{\cdot}{\cdot}$ holds. Hence $\innprd{\cdot}{\cdot}\in W$ and $X\subset W$ and $X=W$. $\blacksquare$
(4) Suppose $V$ is a real inner product space. Then
(a) $\innprd{u+v}{u-v}=\dnorm{u}^2-\dnorm{v}^2$ for every $u,v\in V$.
(b) if $u,v\in V$ have the same norm, then $u+v$ is orthogonal to $u-v$.
(c) part (b) implies that the diagonals of a rhombus are perpendicular to each other.
Proof Since $V$ is a real inner product space, then $\innprd{u}{v}\in\mathbb{R}$ for any $u,v\in V$. Hence $\innprd{u}{v}=\overline{\innprd{v}{u}}=\innprd{v}{u}$. Also note that $\innprd{u}{-v}=\overline{-1}\innprd{u}{v}=-\innprd{u}{v}$. Hence
$$\begin{align*} \innprd{u+v}{u-v} &= \innprd{u}{u-v}+\innprd{v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{v}{u}+\innprd{v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}+\innprd{v}{u}-\innprd{v}{v} \\ &= \innprd{u}{u}-\innprd{u}{v}+\innprd{u}{v}-\innprd{v}{v} \\ &= \innprd{u}{u}-\innprd{v}{v} \\ &= \dnorm{u}^2-\dnorm{v}^2 \end{align*}$$
If $\dnorm{u}=\dnorm{v}$, then $\dnorm{u}^2=\dnorm{v}^2$ and the above equation gives
$$ 0=\dnorm{u}^2-\dnorm{v}^2=\innprd{u+v}{u-v} $$
A rhombus is a quadrilateral whose four sides have the same length. And it can be shown that every rhombus is a parallelogram. On p.174, we saw that the diagonals of a parallogram with sides $u$ and $v$ are given by $u+v$ and $u-v$. Then the above equation shows that the diagonals are perpendicular. $\blacksquare$
(5) Suppose $T\in\lnmpsb(V)$ is such that $\dnorm{Tv}\leq\dnorm{v}$ for every $v\in V$. Then $T-\sqrt{2}I$ is invertible.
Proof As mentioned in the errata, we will assume that $V$ is finite-dimensional. Then, by proposition 3.69, it suffices to show $T-\sqrt{2}I$ is injective. Let $u\in\mathscr{N}(T-\sqrt{2}I)$. Then
$$ 0=(T-\sqrt{2}I)u=Tu-(\sqrt{2}I)u=Tu-\sqrt{2}(Iu)=Tu-\sqrt{2}u $$
and
$$ \sqrt{2}u=Tu $$
Taking the norm of both sides, we get
$$ \sqrt{2}\dnorm{u}=\dnorm{\sqrt{2}u}=\dnorm{Tu}\leq\dnorm{u} $$
If $u\neq0$, then $\dnorm{u}\neq0$ and we can divide both sides by $\dnorm{u}$. This gives $\sqrt{2}\leq1$, a contradiction. Hence it must be that $u=0$. Hence $\mathscr{N}(T-\sqrt{2}I)=\{0\}$. Hence $T-\sqrt{2}I$ is injective (by 3.16). $\blacksquare$
(6) Suppose $u,v\in V$. Then $\innprd{u}{v}=0$ if and only if
$$ \dnorm{u}\leq\dnorm{u+av} $$
for all $a\in\mathbb{F}$.
Proof Suppose $\innprd{u}{v}=0$. Since scaling preserves orthogonality (by W.6.CS.2), then $u,av$ are orthogonal for all $a\in\mathbb{F}$ and the Pythagorean Theorem (6.13) gives
$$ \dnorm{u+av}^2=\dnorm{u}^2+\dnorm{av}^2\geq\dnorm{u}^2 $$
where W.6.CS.4 gives the inequality. Taking the square root of both sides gives the desired result.
In the other direction, suppose $\dnorm{u}\leq\dnorm{u+av}$ for all $a\in\mathbb{F}$. Then
$$\begin{align*} \dnorm{u}^2 &\leq \dnorm{u+av}^2 \\ &= \innprd{u+av}{u+av} \\ &= \innprd{u}{u+av}+\innprd{av}{u+av} \\ &= \innprd{u}{u}+\innprd{u}{av}+\innprd{av}{u}+\innprd{av}{av} \\ &= \dnorm{u}^2+\overline{a}\innprd{u}{v}+a\innprd{v}{u}+a\overline{a}\innprd{v}{v} \\ &= \dnorm{u}^2+\overline{a}\innprd{u}{v}+a\overline{\innprd{u}{v}}+\norm{a}^2\dnorm{v}^2 \\ &= \dnorm{u}^2+2\Re{\big(\overline{a}\innprd{u}{v}\big)}+\norm{a}^2\dnorm{v}^2\tag{by W.4.2} \\ \end{align*}$$
for all $a\in\mathbb{F}$. Subtracting $\dnorm{u}^2+2\Re{\big(\overline{a}\innprd{u}{v}\big)}$ from both sides, we get
$$ -2\Re{\big(\overline{a}\innprd{u}{v}\big)}\leq\norm{a}^2\dnorm{v}^2\tag{6.A.6.1} $$
for all $a\in\mathbb{F}$. Set $a\equiv-t\innprd{u}{v}$ for any $t>0$. Since $\overline{\innprd{u}{v}}\innprd{u}{v}=\norm{\innprd{u}{v}}^2$ (by 4.5, p.119), then
$$ \Re{\big(\overline{a}\innprd{u}{v}\big)}=\Re{\big(\overline{-t\innprd{u}{v}}\innprd{u}{v}\big)}=\Re{\big(\overline{-t}\overline{\innprd{u}{v}}\innprd{u}{v}\big)}=\Re{\big(-t\norm{\innprd{u}{v}}^2\big)}=-t\norm{\innprd{u}{v}}^2 $$
Then 6.A.6.1 becomes
$$ 2t\norm{\innprd{u}{v}}^2\leq\norm{-t\innprd{u}{v}}^2\dnorm{v}^2=t^2\norm{\innprd{u}{v}}^2\dnorm{v}^2 $$
for any $t>0$. Dividing both sides by $t$, we get
$$ 2\norm{\innprd{u}{v}}^2\leq t\norm{\innprd{u}{v}}^2\dnorm{v}^2 $$
for any $t>0$. If $v=0$, then $\innprd{u}{v}=0$ (by 6.7.c) as desired. If $v\neq0$, then set $t\equiv\frac1{\dnorm{v}^2}$ so that
$$ 2\norm{\innprd{u}{v}}^2\leq\norm{\innprd{u}{v}}^2 $$
If $\innprd{u}{v}\neq0$, then divide both sides by $\norm{\innprd{u}{v}}^2$ to get $2\leq1$, a contradiction. Hence it must be that $\innprd{u}{v}=0$. $\blacksquare$
(7) Suppose $u,v\in V$. Then $\dnorm{au+bv}=\dnorm{bu+av}$ for all $a,b\in\mathbb{R}$ if and only if $\dnorm{u}=\dnorm{v}$.
Proof Suppose $\dnorm{au+bv}=\dnorm{bu+av}$ for all $a,b\in\mathbb{R}$. Set $a\equiv1$ and $b\equiv0$ to get
$$\begin{align*} \dnorm{u}^2 &= \dnorm{1\cdot u+0\cdot v}^2 \\ &= \dnorm{0\cdot u+1\cdot v}^2 \\ &= \dnorm{v}^2 \\ \end{align*}$$
In the other direction, suppose $\dnorm{u}=\dnorm{v}$. For any $a,b\in\mathbb{R}$, we have
$$\begin{align*} \dnorm{av+bu}^2 &= \innprd{av+bu}{av+bu} \\ &= \innprd{av}{av+bu}+\innprd{bu}{av+bu} \\ &= \innprd{av}{av}+\innprd{av}{bu}+\innprd{bu}{av}+\innprd{bu}{bu} \\ &= a^2\innprd{v}{v}+ab\innprd{v}{u}+ab\innprd{u}{v}+b^2\innprd{u}{u} \\ &= a^2\dnorm{v}^2+ab\innprd{v}{u}+ab\innprd{u}{v}+b^2\dnorm{u}^2 \\ \end{align*}$$
Similarly
$$\begin{align*} \dnorm{au+bv}^2 &= \innprd{au+bv}{au+bv} \\ &= \innprd{au}{au}+\innprd{au}{bv}+\innprd{bv}{au}+\innprd{bv}{bv} \\ &= a^2\innprd{u}{u}+ab\innprd{u}{v}+ab\innprd{v}{u}+b^2\innprd{v}{v} \\ &= a^2\dnorm{u}^2+ab\innprd{u}{v}+ab\innprd{v}{u}+b^2\dnorm{v}^2 \\ &= a^2\dnorm{v}^2+ab\innprd{u}{v}+ab\innprd{v}{u}+b^2\dnorm{u}^2\tag{6.A.7.1} \\ &= a^2\dnorm{v}^2+ab\innprd{v}{u}+ab\innprd{u}{v}+b^2\dnorm{u}^2 \\ &= \dnorm{av+bu}^2 \\ &= \dnorm{bu+av}^2 \\ \end{align*}$$
In the 6.A.7.1, we twice made the substitution $\dnorm{u}=\dnorm{v}$. $\blacksquare$
(8) Suppose $u,v\in V$ and $\dnorm{u}=\dnorm{v}=1$ and $\innprd{u}{v}=1$. Then $u=v$.
Proof Note that
$$\begin{align*} \dnorm{u-v}^2 &= \innprd{u-v}{u-v} \\ &= \innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2-\innprd{u}{v}-\overline{\innprd{u}{v}}+\dnorm{v}^2 \\ &= 1-1-1+1 \\ &= 0 \end{align*}$$
Then the definiteness property of inner products implies that $u-v=0$. $\blacksquare$
(9) Suppose $u,v\in V$ and $\dnorm{u}\leq1$ and $\dnorm{v}\leq1$. Then
$$ \sqrt{1-\dnorm{u}^2}\sqrt{1-\dnorm{v}^2}\leq1-\norm{\innprd{u}{v}} $$
Proof Multiplying the inequalities $\dnorm{u}\leq1$ and $\dnorm{v}\leq1$, we get
$$ \dnorm{u}\dnorm{v}\leq 1\cdot1=1 $$
Subtracting $\dnorm{u}\dnorm{v}$ from both sides, we get
$$ 0\leq 1-\dnorm{u}\dnorm{v} $$
The Cauchy-Schwarz Inequality (6.15) is $\dnorm{u}\dnorm{v}\geq\norm{\innprd{u}{v}}$. Equivalently $-\dnorm{u}\dnorm{v}\leq-\norm{\innprd{u}{v}}$. Hence
$$ 0\leq 1-\dnorm{u}\dnorm{v}\leq1-\norm{\innprd{u}{v}} $$
Hence it suffices to show that
$$ \sqrt{1-\dnorm{u}^2}\sqrt{1-\dnorm{v}^2}\leq1-\dnorm{u}\dnorm{v}\tag{6.A.9.1} $$
Since both sides are nonnegative, then squaring them preserves the inequality. Note that
$$\begin{align*} \Prn{\sqrt{1-\dnorm{u}^2}\sqrt{1-\dnorm{v}^2}}^2 &= \prn{1-\dnorm{u}^2}\prn{1-\dnorm{v}^2} \\ &= 1-\dnorm{v}^2-\dnorm{u}^2+\dnorm{u}^2\dnorm{v}^2 \end{align*}$$
and
$$\begin{align*} \prn{1-\dnorm{u}\dnorm{v}}^2 &= 1-\dnorm{u}\dnorm{v}-\dnorm{u}\dnorm{v}+\dnorm{u}^2\dnorm{v}^2 \\ &= 1-2\dnorm{u}\dnorm{v}+\dnorm{u}^2\dnorm{v}^2 \\ \end{align*}$$
Hence 6.A.9.1 is equivalent to
$$ 1-\dnorm{v}^2-\dnorm{u}^2+\dnorm{u}^2\dnorm{v}^2\leq 1-2\dnorm{u}\dnorm{v}+\dnorm{u}^2\dnorm{v}^2 $$
or
$$ -\dnorm{v}^2-\dnorm{u}^2\leq -2\dnorm{u}\dnorm{v} $$
or
$$\begin{align*} 0 &\leq -2\dnorm{u}\dnorm{v}+\dnorm{v}^2+\dnorm{u}^2 \\ &= \dnorm{u}^2-2\dnorm{u}\dnorm{v}+\dnorm{v}^2 \\ &= \prn{\dnorm{u}-\dnorm{v}}^2 \\ \end{align*}$$
which we know is true. $\blacksquare$
(10) Find vectors $u.v\in\mathbb{R}^2$ such that $u$ is a scalar multiple of $(1,3)$, $v$ is orthogonal to $(1,3)$, and $(1,2)=u+v$.
Solution Let’s first try $u=(1,3)$ and $v=(-3,1)$. Then $u+v=(-2,4)$. Not quite. But geometrically we know the correct $u,v$ will be scalar multiples of these. Hence
$$ (1,2)=a(1,3)+b(-3,1)=(a,3a)+(-3b,b)=(a-3b,3a+b) $$
This becomes the system
$$ a-3b=1 \\ 3a+b=2 $$
or
$$ \begin{bmatrix}1&-3&1\\3&1&2\end{bmatrix} \rightarrow \begin{bmatrix}1&-3&1\\0&10&-1\end{bmatrix} \rightarrow \begin{bmatrix}1&-3&1\\0&1&-\frac1{10}\end{bmatrix} \rightarrow \begin{bmatrix}1&0&1-\frac3{10}\\0&1&-\frac1{10}\end{bmatrix} \rightarrow \begin{bmatrix}1&0&\frac7{10}\\0&1&-\frac1{10}\end{bmatrix} $$
So define
$$ u\equiv a(1,3)=\frac7{10}(1,3)=\Big(\frac7{10},\frac{21}{10}\Big) $$
and
$$ v\equiv b(-3,1)=-\frac1{10}(-3,1)=\Big(\frac3{10},-\frac1{10}\Big) $$
Clearly $u$ is a scalar multiple of $(1,3)$. And we can check that $v$ is orthogonal to $(1,3)$:
$$ \innprd{v}{(1,3)}=\innprdBg{\Big(\frac3{10},-\frac1{10}\Big)}{(1,3)}=\frac3{10}\cdot1+\Prn{-\frac1{10}}\cdot3=\frac3{10}-\frac3{10}=0 $$
In the second equality, we implemented the inner product with the dot product. Since this is zero, then $v$ is orthogonal with $(1,3)$. We can also see this geometrically:
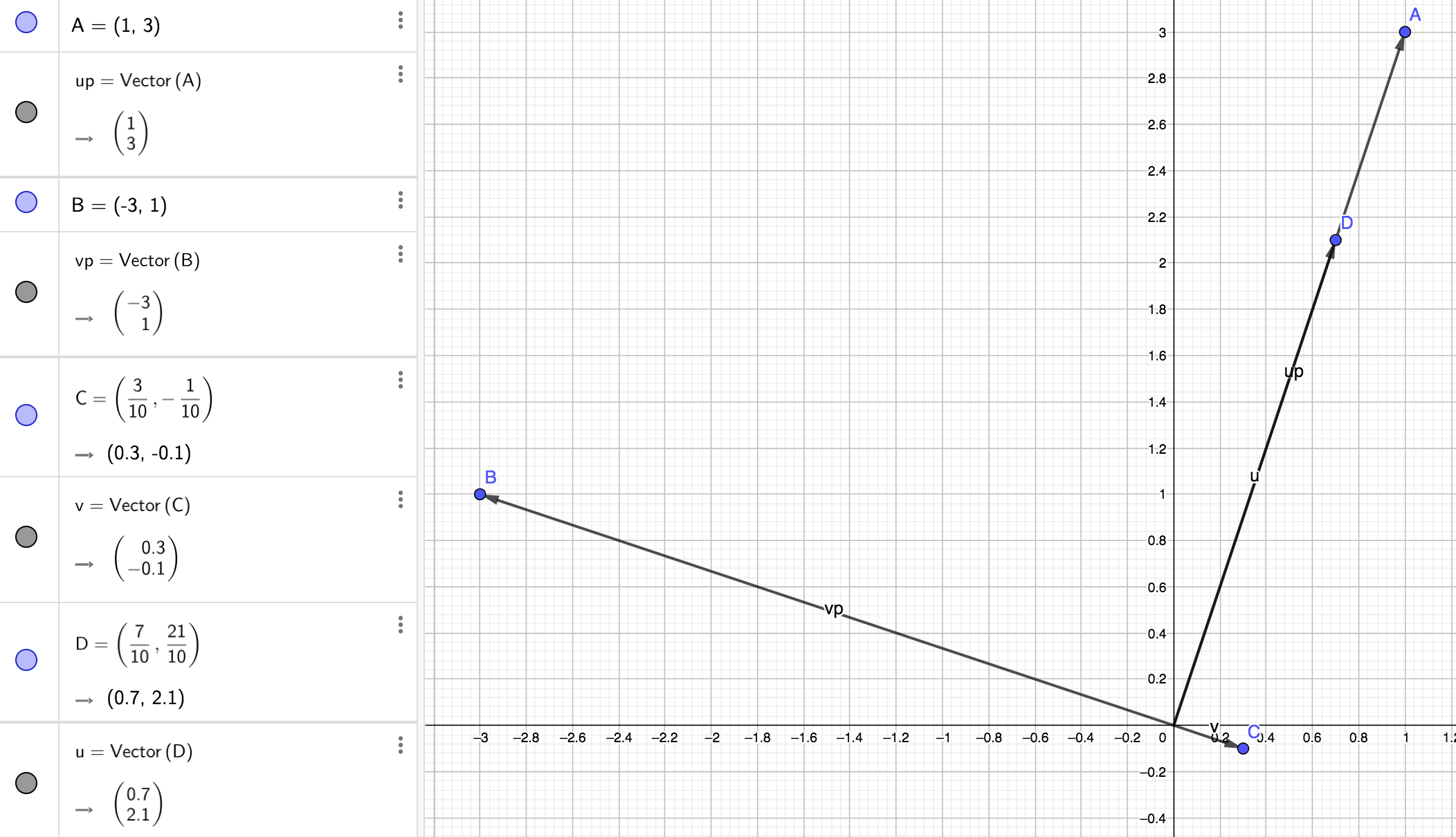
We also check that
$$ u+v=\Big(\frac7{10},\frac{21}{10}\Big)+\Big(\frac3{10},-\frac1{10}\Big)=\Big(\frac{10}{10},\frac{20}{10}\Big)=(1,2)\quad\blacksquare $$
(11) For all positive numbers $a,b,c,d$, this holds:
$$ 16\leq\prn{a+b+c+d}\Big(\frac1a+\frac1b+\frac1c+\frac1d\Big) \\ $$
Proof Define
$$ u\equiv\prn{\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}}\in\mathbb{R}^4 $$
Using the dot product, the norm of $u$ is
$$\begin{align*} \dnorm{u}^2 &= u\cdot u \\ &= \prn{\sqrt{a}}^2+\prn{\sqrt{b}}^2+\prn{\sqrt{c}}^2+\prn{\sqrt{d}}^2 \\ &= a+b+c+d \end{align*}$$
Similarly
$$ v\equiv\Bigg(\sqrt{\frac1a},\sqrt{\frac1b},\sqrt{\frac1c},\sqrt{\frac1d}\Bigg)\in\mathbb{R}^4 $$
and
$$\begin{align*} \dnorm{v}^2 &= v\cdot v \\ &= \Prngg{\sqrt{\frac1a}}^2+\Prngg{\sqrt{\frac1b}}^2+\Prngg{\sqrt{\frac1c}}^2+\Prngg{\sqrt{\frac1d}}^2 \\ &= \frac1a+\frac1b+\frac1c+\frac1d \\ \end{align*}$$
Also note that
$$\begin{align*} \innprd{u}{v} &= u\cdot v \\ &= \sqrt{a}\cdot\sqrt{\frac1a}+\sqrt{b}\cdot\sqrt{\frac1b}+\sqrt{c}\cdot\sqrt{\frac1c}+\sqrt{d}\cdot\sqrt{\frac1d} \\ &= \sqrt{a\cdot\frac1a}+\sqrt{b\cdot\frac1b}+\sqrt{c\cdot\frac1c}+\sqrt{d\cdot\frac1d} \\ &= 4 \end{align*}$$
Then Cauchy-Schwarz (6.15) gives
$$ 16=\norm{4}^2=\norm{\innprd{u}{v}}^2\leq\prn{\dnorm{u}\dnorm{v}}^2=\dnorm{u}^2\dnorm{v}^2=\prn{a+b+c+d}\Big(\frac1a+\frac1b+\frac1c+\frac1d\Big) $$
$\blacksquare$
(12) For all positive integers $n$ and all real numbers $x_1,\dots,x_n$, this holds:
$$ \prn{x_1+\dotsb+x_n}^2\leq n\prn{x_1^2+\dotsb+x_n^2} $$
Proof Define
$$ u\equiv\prn{x_1,\dots,x_n}\in\mathbb{R}^n \quad\quad\quad\quad v\equiv(1,\dots,1)\in\mathbb{R}^n $$
Using the dot product, the norms are
$$ \dnorm{u}^2 = u\cdot u= \sum_{j=1}^nx_j^2 \quad\quad\quad\quad \dnorm{v}^2 = v\cdot v= \sum_{j=1}^n1^2= n $$
Also note that
$$ \innprd{u}{v} = u\cdot v= \sum_{j=1}^nx_j\cdot1= \sum_{j=1}^nx_j $$
Then Cauchy-Schwarz (6.15) gives
$$ \Prn{\sum_{j=1}^nx_j}^2=\normB{\sum_{j=1}^nx_j}^2=\norm{\innprd{u}{v}}^2\leq\prn{\dnorm{u}\dnorm{v}}^2=\dnorm{v}^2\dnorm{u}^2=n\cdot\sum_{j=1}^nx_j^2 $$
$\blacksquare$
(13) Suppose $u,v$ are nozero vectors in $\mathbb{R}^2$. Then
$$ \innprd{u}{v}=\dnorm{u}\dnorm{v}\cos\theta $$
where $\theta$ is the angle between $u$ and $v$ (thinking of $u$ and $v$ as arrows with initial point at the origin).
Hint: Draw the triangle formed by $u,v,$ and $u-v$; then use the law of cosines.
Proof Here’s the triangle:
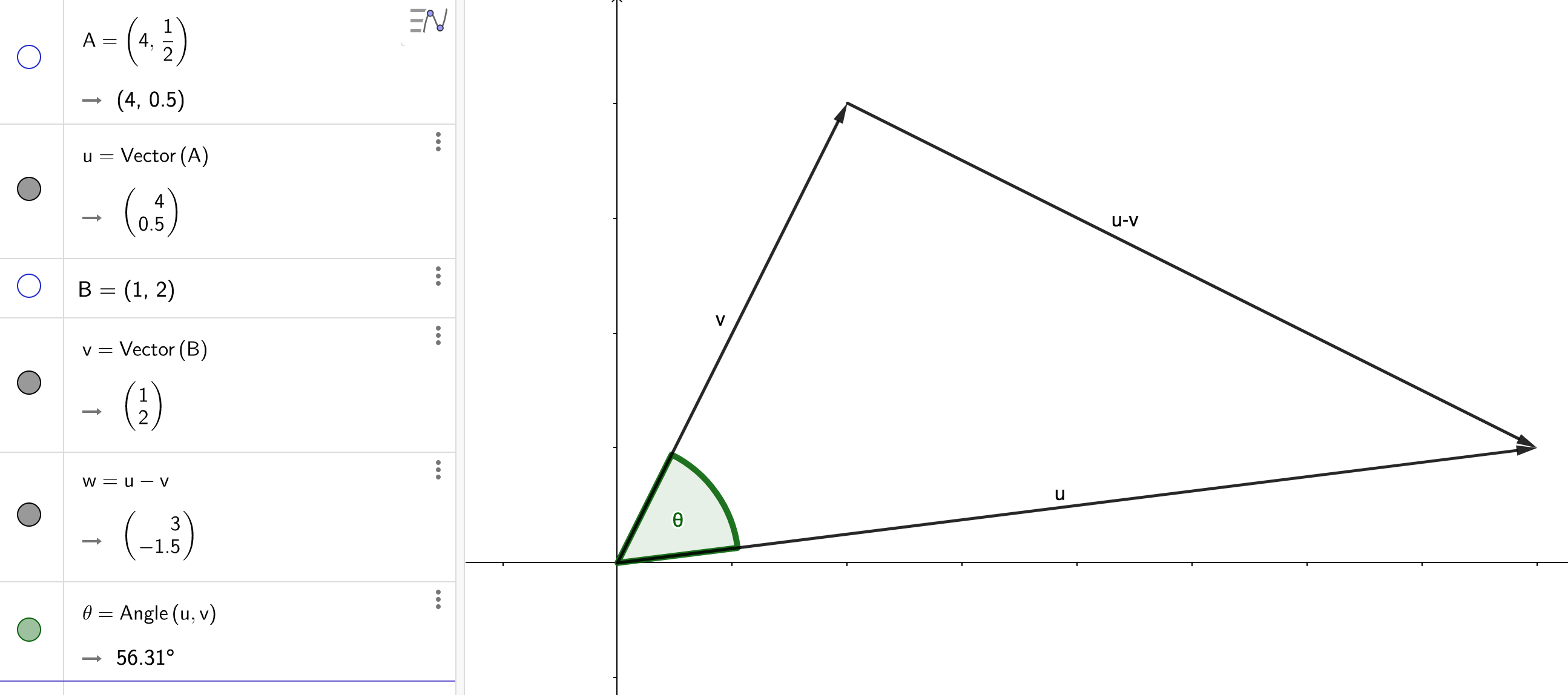
The law of cosines states that
$$ \dnorm{x-y}^2=\dnorm{x}^2+\dnorm{y}^2-2\dnorm{x}\dnorm{y}\cos{\theta} $$
Computing this same length with inner products, we get
$$\begin{align*} \dnorm{x-y}^2 &= \innprd{x-y}{x-y} \\ &= \innprd{x}{x-y}+\innprd{-y}{x-y} \\ &= \innprd{x}{x}+\innprd{x}{-y}+\innprd{-y}{x}+\innprd{-y}{-y} \\ &= \innprd{x}{x}-\innprd{x}{y}-\innprd{y}{x}+\innprd{y}{y} \\ &= \dnorm{x}^2+\dnorm{y}^2-2\innprd{x}{y} \\ \end{align*}$$
Hence
$$ \dnorm{x}^2+\dnorm{y}^2-2\innprd{x}{y}=\dnorm{x-y}^2=\dnorm{x}^2+\dnorm{y}^2-2\dnorm{x}\dnorm{y}\cos{\theta} $$
Now subtract $\dnorm{x}^2+\dnorm{y}^2$ from both sides of this equation, and then divide both sides by $-2$, to get
$$ \innprd{x}{y}=\dnorm{x}\dnorm{y}\cos{\theta} $$
$\blacksquare$
(14) The angle between two vectors (thought of as arrows with initial point at the origin) in $\mathbb{R}^2$ or $\mathbb{R}^3$ can be defined geometrically. However, geometry is not as clear in $\mathbb{R}^n$ for $n>3$. Thus the angle between two nonzero vectors $x,y\in\mathbb{R}^n$ is defined to be
$$ \arccos{\frac{\innprd{x}{y}}{\dnorm{x}\dnorm{y}}} $$
where the motivation for this definition comes from the previous exercise. Explain why the Cauchy–Schwarz Inequality is needed to show that this definition makes sense.
Explanation Since the range of the cosine function is the segment $[-1,1]$, then the domain of the $\arccos$ function is the segment $[-1,1]$. So this definition will only make sense if
$$ -1\leq\frac{\innprd{x}{y}}{\dnorm{x}\dnorm{y}}\leq1 $$
for all vectors $x,y\in\mathbb{R}^n$. Equivalently
$$ 1\geq\normBgg{\frac{\innprd{x}{y}}{\dnorm{x}\dnorm{y}}}=\frac{\norm{\innprd{x}{y}}}{\norm{\dnorm{x}\dnorm{y}}}=\frac{\norm{\innprd{x}{y}}}{\dnorm{x}\dnorm{y}} $$
Multiplying both sides by $\dnorm{x}\dnorm{y}$, we see that this is the Cauchy-Schwarz Inequality. $\blacksquare$
(15) For all real numbers $a_1,\dots,a_n$ and $b_1,\dots,b_n$, this holds:
$$ \Big(\sum_{j=1}^na_jb_j\Big)^2\leq\Big(\sum_{j=1}^nja_j^2\Big)\Big(\sum_{j=1}^n\frac{b_j^2}{j}\Big) $$
Proof We implement the inner product with the dot product:
$$\begin{align*} \Big(\sum_{j=1}^na_jb_j\Big)^2 &= \normBgg{\sum_{j=1}^na_jb_j\Prn{\frac{\sqrt{j}}{\sqrt{j}}}}^2 \\ &= \normBgg{\sum_{j=1}^n\prn{\sqrt{j}a_j}\Prn{\frac{b_j}{\sqrt{j}}}}^2 \\ &= \normBgg{\innprdBg{\prn{\sqrt{1}a_1,\sqrt{2}a_2,\dots,\sqrt{n}a_n}}{\Prn{\frac{b_1}{\sqrt{1}},\frac{b_2}{\sqrt{2}},\dots,\frac{b_n}{\sqrt{n}}}}}^2 \\ &\leq \dnormB{\prn{\sqrt{1}a_1,\sqrt{2}a_2,\dots,\sqrt{n}a_n}}^2\dnormBgg{\Prn{\frac{b_1}{\sqrt{1}},\frac{b_2}{\sqrt{2}},\dots,\frac{b_n}{\sqrt{n}}}}^2 \\ &=\Bigg(\sum_{j=1}^n\prn{\sqrt{j}a_j}^2\Bigg)\Bigg(\sum_{j=1}^n\Prn{\frac{b_j}{\sqrt{j}}}^2\Bigg) \\ &=\Big(\sum_{j=1}^nja_j^2\Big)\Big(\sum_{j=1}^n\frac{b_j^2}{j}\Big) \end{align*}$$
where the inequality comes from the Cauchy-Schwarz inequality. $\blacksquare$
(16) Suppose $u,v\in V$ are such that
$$ \dnorm{u}=3 \quad\quad\quad \dnorm{u+v}=4 \quad\quad\quad \dnorm{u-v}=6 $$
What number does $\dnorm{v}$ equal?
Solution From the parallelogram equality, we have
$$\begin{align*} \dnorm{v}^2 &= \frac{\dnorm{u+v}^2+\dnorm{u-v}^2-2\dnorm{u}^2}{2} \\ &= \frac{16+36-18}{2} \\ &= 17 \end{align*}$$
Since the norm is always nonnegative, then $\dnorm{v}=\sqrt{17}$. $\blacksquare$
(17) Prove or disprove: there is an inner product on $\mathbb{R}^2$ such that the associated norm is given by
$$ \dnormb{(x,y)}=\max\{x,y\} $$
for all $(x,y)\in\mathbb{R}^2$.
Counterexample The norm of such an inner product would have to satisfy the Parallelogram Equality:
$$ \dnorm{u+v}^2+\dnorm{u-v}^2=2\prn{\dnorm{u}^2+\dnorm{v}^2} $$
Set $u=(1,0)$ and $v=(0,1)$. Then $u+v=(1,1)$ and $u-v=(1,-1)$ and
$$\begin{align*} \dnorm{u+v}^2+\dnorm{u-v}^2 &= \dnorm{(1,1)}^2+\dnorm{(1,-1)}^2 \\ &= \prn{\max\{1,1\}}^2+\prn{\max\{1,-1\}}^2 \\ &= 1^2+1^2 \\ &= 2 \end{align*}$$
But
$$\begin{align*} 2\prn{\dnorm{u}^2+\dnorm{v}^2} &= 2\Prn{\prn{\max\{1,0\}}^2+\prn{\max\{0,1\}}^2} \\ &= 2(1+1) \\ &= 4 \quad\blacksquare \end{align*}$$
(18) Suppose $p>0$. Then there is an inner product on $\mathbb{R}^2$ such that the associated norm is given by
$$ \dnormb{(x,y)}=(x^p+y^p)^{1/p} $$
for all $(x,y)\in\mathbb{R}^2$ if and only if $p=2$.
Proof
(19) Suppose $V$ is a real inner product space. Then
$$ \innprd{u}{v}=\frac{\dnorm{u+v}^2-\dnorm{u-v}^2}{4} $$
for all $u,v\in V$.
Proof For any $u,v\in V$, we have
$$\begin{align*} \dnorm{u+v}^2 &= \innprd{u+v}{u+v} \\ &= \innprd{u}{u+v}+\innprd{v}{u+v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{v}{u}+\dnorm{v}^2 \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{u}{v}+\dnorm{v}^2 \\ &= \dnorm{u}^2+2\innprd{u}{v}+\dnorm{v}^2 \end{align*}$$
Similarly
$$\begin{align*} \dnorm{u-v}^2 &= \innprd{u-v}{u-v} \\ &= \innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{v}{u}+\dnorm{v}^2 \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{u}{v}+\dnorm{v}^2 \\ &= \dnorm{u}^2-2\innprd{u}{v}+\dnorm{v}^2 \end{align*}$$
Hence
$$ \frac{\dnorm{u+v}^2-\dnorm{u-v}^2}{4} = \frac{4\innprd{u}{v}}{4} = \innprd{u}{v} \quad\blacksquare $$
(20) Suppose $V$ is a complex inner product space. Then
$$ \innprd{u}{v}=\frac{\dnorm{u+v}^2-\dnorm{u-v}^2+\dnorm{u+iv}^2i-\dnorm{u-iv}^2i}{4} $$
for all $u,v\in V$.
Proof For any $u,v\in V$, we have
$$\begin{align*} \dnorm{u+v}^2 &= \innprd{u+v}{u+v} \\ &= \innprd{u}{u+v}+\innprd{v}{u+v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{v}{u}+\dnorm{v}^2 \\ \end{align*}$$
Similarly
$$\begin{align*} \dnorm{u-v}^2 &= \innprd{u-v}{u-v} \\ &= \innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{v}{u}+\dnorm{v}^2 \\ \end{align*}$$
Hence
$$ \dnorm{u+v}^2-\dnorm{u-v}^2 = 2\innprd{u}{v}+2\innprd{v}{u}\tag{6.A.20.1} $$
Next
$$\begin{align*} i\dnorm{u+iv}^2 &= i\innprd{u+iv}{u+iv} \\ &= i\innprd{u}{u+iv}+i\innprd{iv}{u+iv} \\ &= i\innprd{u}{u}+i\innprd{u}{iv}+i\innprd{iv}{u}+i\innprd{iv}{iv} \\ &= i\innprd{u}{u}+i\overline{i}\innprd{u}{v}+i^2\innprd{v}{u}+i^2\overline{i}\innprd{v}{v} \\ &= i\innprd{u}{u}+i(-i)\innprd{u}{v}-\innprd{v}{u}-(-i)\innprd{v}{v} \\ &= i\innprd{u}{u}-i^2\innprd{u}{v}-\innprd{v}{u}+i\innprd{v}{v} \\ &= i\dnorm{u}^2+\innprd{u}{v}-\innprd{v}{u}+i\dnorm{v}^2 \\ \end{align*}$$
Similarly
$$\begin{align*} i\dnorm{u-iv}^2 &= i\innprd{u-iv}{u-iv} \\ &= i\innprd{u}{u-iv}+i\innprd{-iv}{u-iv} \\ &= i\innprd{u}{u}+i\innprd{u}{-iv}+i\innprd{-iv}{u}+i\innprd{-iv}{-iv} \\ &= i\innprd{u}{u}+i(\overline{-i})\innprd{u}{v}+i(-i)\innprd{v}{u}+i(-i)(\overline{-i})\innprd{v}{v} \\ &= i\innprd{u}{u}+ii\innprd{u}{v}-i^2\innprd{v}{u}-i^2i\innprd{v}{v} \\ &= i\innprd{u}{u}-\innprd{u}{v}+\innprd{v}{u}+i\innprd{v}{v} \\ &= i\dnorm{u}^2-\innprd{u}{v}+\innprd{v}{u}+i\dnorm{v}^2 \\ \end{align*}$$
Hence
$$ i\dnorm{u+iv}^2-i\dnorm{u-iv}^2 = 2\innprd{u}{v}-2\innprd{v}{u}\tag{6.A.20.2} $$
Combining 6.A.20.1 and 6.A.20.2, we get
$$\begin{align*} \frac{\dnorm{u+v}^2-\dnorm{u-v}^2+\dnorm{u+iv}^2i-\dnorm{u-iv}^2i}{4} &= \frac{2\innprd{u}{v}+2\innprd{v}{u}+2\innprd{u}{v}-2\innprd{v}{u}}{4} \\ &= \frac{4\innprd{u}{v}}{4} \\ &= \innprd{u}{v}\quad\blacksquare \end{align*}$$
(22) The square of an average is less than or equal to the average of the squares. More precisely, for any $x_1,\dots,x_n\in\mathbb{R}$, we have
$$ \Prn{\frac1n\sum_{j=1}^nx_j}^2\leq\frac1n\sum_{j=1}^nx_j^2 $$
Proof Exercise 6.A.12 gives the inequality:
$$ \Prn{\frac1n\sum_{j=1}^nx_j}^2=\frac1{n^2}\Prn{\sum_{j=1}^nx_j}^2\leq\frac1{n^2}\cdot n\cdot\sum_{j=1}^nx_j^2=\frac1n\sum_{j=1}^nx_j^2 $$
$\blacksquare$
(23) Suppose $V_1,\dots,V_m$ are inner product spaces. Then the equation
$$ \innprdbg{(u_1,\dots,u_m)}{(v_1,\dots,v_m)} \equiv \sum_{j=1}^m\innprd{u_j}{v_j} $$
defines an inner product on $V_1\times\dotsb\times V_m$.
In the expression above on the right, $\innprd{u_1}{v_1}$ denotes the inner product on $V_1$,…, $\innprd{u_m}{v_m}$ denotes the inner product on $V_m$. Each of the spaces $V_1,\dots,V_m$ may have a different inner product, even though the same notation is used here.
Proof Let $u,v,w\in V_1\times V_m$. Then $u=(u_1,\dots,u_m)$ for some $u_j\in V_j$. And similarly for $v$ and $w$. Then definition 3.71, p.91 gives
$$\begin{align*} u+v &= (u_1,\dots,u_m)+(v_1,\dots,v_m)=(u_1+v_1,\dots,u_m+v_m) \\\\ \lambda u &= \lambda (u_1,\dots,u_m) = (\lambda u_1,\dots,\lambda u_m) \end{align*}$$
Positivity: the inequality holds because $\innprd{v_j}{v_j}\geq0$ for $j=1,\dots,m$:
$$ \innprd{v}{v} = \innprdbg{(v_1,\dots,v_m)}{(v_1,\dots,v_m)} = \sum_{j=1}^m\innprd{v_j}{v_j}\geq0 \\ $$
Definiteness: Suppose $v=0$. Then $v_j=0$ for $j=1,\dots,m$. Hence $\innprd{v_j}{v_j}=0$ for $j=1,\dots,m$ and
$$ \innprd{v}{v}=\innprdbg{(v_1,\dots,v_m)}{(v_1,\dots,v_m)} = \sum_{j=1}^m\innprd{v_j}{v_j}=0 $$
Conversely, suppose $\innprd{v}{v}=0$. Then
$$ 0=\innprd{v}{v}=\innprdbg{(v_1,\dots,v_m)}{(v_1,\dots,v_m)} = \sum_{j=1}^m\innprd{v_j}{v_j} $$
Note that the positivity of each $V_j$ implies $\innprd{v_j}{v_j}\geq0$ for $j=1,\dots,m$. Hence if $\innprd{v_k}{v_k}>0$ for some $k$, then the above equality fails. So it must be that $\innprd{v_j}{v_j}=0$ for $j=1,\dots,m$. Then the definiteness of each $V_j$ implies that $v_j=0$ for $j=1,\dots,m$. Hence $v=(v_1,\dots,v_m)=(0,\dots,0)=0$.
Additivity in the first slot: the third equality holds because $\innprd{u_j+v_j}{w_j}=\innprd{u_j}{w_j}+\innprd{v_j}{w_j}$ for $j=1,\dots,m$:
$$\begin{align*} \innprd{u+v}{w} &= \innprdbg{(u_1+v_1,\dots,u_m+v_m)}{(w_1,\dots,w_m)} \\ &= \sum_{j=1}^m\innprd{u_j+v_j}{w_j} \\ &= \sum_{j=1}^m\prn{\innprd{u_j}{w_j}+\innprd{v_j}{w_j}} \\ &= \sum_{j=1}^m\innprd{u_j}{w_j}+\sum_{j=1}^m\innprd{v_j}{w_j} \\ &= \innprdbg{(u_1,\dots,u_m)}{(w_1,\dots,w_m)}+\innprdbg{(v_1,\dots,v_m)}{(w_1,\dots,w_m)} \\ &= \innprd{u}{w}+\innprd{v}{w} \end{align*}$$
Homogeneity in the first slot:
$$\begin{align*} \innprd{\lambda u}{v} &= \innprdbg{(\lambda u_1,\dots,\lambda u_m)}{(v_1,\dots,v_m)} \\ &= \sum_{j=1}^m\innprd{\lambda u_j}{v_j} \\ &= \sum_{j=1}^m\lambda\innprd{u_j}{v_j} \\ &= \lambda\sum_{j=1}^m\innprd{u_j}{v_j} \\ &= \lambda\innprdbg{(u_1,\dots,u_m)}{(v_1,\dots,v_m)} \\ &= \lambda\innprd{u}{v} \end{align*}$$
Conjugate symmetry:
$$\begin{align*} \innprd{u}{v} &= \innprdbg{(u_1,\dots,u_m)}{(v_1,\dots,v_m)} \\ &= \sum_{j=1}^m\innprd{u_j}{v_j} \\ &= \sum_{j=1}^m\overline{\innprd{v_j}{u_j}} \\ &= \overline{\sum_{j=1}^m\innprd{v_j}{u_j}}\tag{by 4.5, p.119} \\ &= \overline{\innprdbg{(v_1,\dots,v_m)}{(u_1,\dots,u_m)}} \\ &= \overline{\innprd{v}{u}}\quad\blacksquare \end{align*}$$
(24) Suppose $S\in\lnmpsb(V)$ is an injective operator on $V$. Define $\innprd{\cdot}{\cdot}_1$ by
$$ \innprd{u}{v}_1\equiv\innprd{Su}{Sv} $$
for $u,v\in V$. Then $\innprd{\cdot}{\cdot}_1$ is an inner product on $V$.
Proof Positivity: Let $v\in V$. Then the positivity of $\innprd{\cdot}{\cdot}$ implies that $\innprd{v}{v}_1=\innprd{Sv}{Sv}\geq0$.
Definiteness: The linearity of $S$ implies that $S(0)=0$ (by 3.11). And the definiteness of $\innprd{\cdot}{\cdot}$ gives the last equality:
$$ \innprd{0}{0}_1=\innprd{S(0)}{S(0)}=\innprd{0}{0}=0 $$
If $0=\innprd{v}{v}_1=\innprd{Sv}{Sv}$, then the definiteness of $\innprd{\cdot}{\cdot}$ implies that $Sv=0$. Then the injectivity of $S$ implies that $v=0$ (by 3.16).
Additivity in the first slot: The third equality follows from first slot additivity of $\innprd{\cdot}{\cdot}$:
$$\begin{align*} \innprd{u+v}{w}_1 &= \innprd{S(u+v)}{Sw} \\ &= \innprd{Su+Sv}{Sw} \\ &= \innprd{Su}{Sw}+\innprd{Sv}{Sw} \\ &= \innprd{u}{w}_1+\innprd{v}{w}_1 \\ \end{align*}$$
Homogeneity in the first slot:
$$\begin{align*} \innprd{\lambda u}{w}_1 &= \innprd{S(\lambda u)}{Sw} \\ &= \innprd{\lambda Su}{Sw} \\ &= \lambda\innprd{Su}{Sw} \\ &= \lambda\innprd{u}{w}_1 \\ \end{align*}$$
Conjugate symmetry: $\innprd{u}{v}_1=\innprd{Su}{Sv}=\overline{\innprd{Sv}{Su}}=\overline{\innprd{v}{u}_1}$. $\blacksquare$
(25) Suppose $S\in\lnmpsb(V)$ is not injective. Define $\innprd{\cdot}{\cdot}_1$ as in the previous exercise. Explain why $\innprd{\cdot}{\cdot}_1$ is not an inner product on $V$.
Explanation Since $S$ is not injective, then there exists a nonzero $u\in V$ such that $Su=0$. Hence $\innprd{u}{u}_1=\innprd{Su}{Su}=0$. Hence $\innprd{\cdot}{\cdot}_1$ doesn’t satisfy definiteness. $\blacksquare$
(26) Suppose $f,g$ are differentiable functions from $\mathbb{R}$ to $\mathbb{R}^n$.
(a) Then
$$ \innprdbg{f(t)}{g(t)}'=\innprdbg{f'(t)}{g(t)}+\innprdbg{f(t)}{g'(t)} $$
(b) Suppose $c>0$ and $\dnorm{f(t)}=c$ for every $t\in\mathbb{R}$. Then $\innprdbg{f’(t)}{f(t)}=0$ for every $t\in\mathbb{R}$.
(c) Interpret the result in part (b) geometrically in terms of the tangent vector to a curve lying on a sphere in $\mathbb{R}^n$ centered at the origin.
For the exercise above, a function $f:\mathbb{R}\mapsto\mathbb{R}^n$ is called differentiable if there exists differentiable functions $f_1,\dots,f_n$ from $\mathbb{R}$ to $\mathbb{R}$ such that $f(t)=\prn{f_1(t),\dots,f_n(t)}$ for each $t\in\mathbb{R}$. Furthermore, for each $t\in\mathbb{R}$, the derivative $f’(t)\in\mathbb{R}^n$ is defined by
$$ f'(t)\equiv\prn{f_1'(t),\dots,f_1'(t)} $$
Proof Part (a):
$$\begin{align*} \innprdbg{f'(t)}{g(t)}+\innprdbg{f(t)}{g'(t)} &= \innprdbg{\prn{f_1'(t),\dots,f_n'(t)}}{\prn{g_1(t),\dots,g_n(t)}} \\ &+ \innprdbg{\prn{f_1(t),\dots,f_n(t)}}{\prn{g_1'(t),\dots,g_n'(t)}} \\ &= \sum_{j=1}^nf_j'(t)g_j(t)+\sum_{j=1}^nf_j(t)g_j'(t) \\ &= \sum_{j=1}^n\prn{f_j'(t)g_j(t)+f_j(t)g_j'(t)} \\ &= \sum_{j=1}^n(f_jg_j)'(t)\tag{by the product rule} \\ &= \Prn{\sum_{j=1}^n(f_jg_j)(t)}' \\ &= \Prn{\sum_{j=1}^nf_j(t)g_j(t)}' \\ &= \innprdbg{\prn{f_1(t),\dots,f_n(t)}}{\prn{g_1(t),\dots,g_n(t)}}' \\ &= \innprdbg{f(t)}{g(t)}' \end{align*}$$
Part (b):
$$\begin{align*} 2\innprdbg{f'(t)}{f(t)} &= \innprdbg{f'(t)}{f(t)}+\innprdbg{f'(t)}{f(t)} \\ &= \innprdbg{f'(t)}{f(t)}+\overline{\innprdbg{f(t)}{f'(t)}} \\ &= \innprdbg{f'(t)}{f(t)}+\innprdbg{f(t)}{f'(t)} \\ &= \innprdbg{f(t)}{f(t)}'\tag{by part (a)} \\ &= \prn{\dnorm{f(t)}^2}' \\ &= (c^2)' \\ &= 0 \end{align*}$$
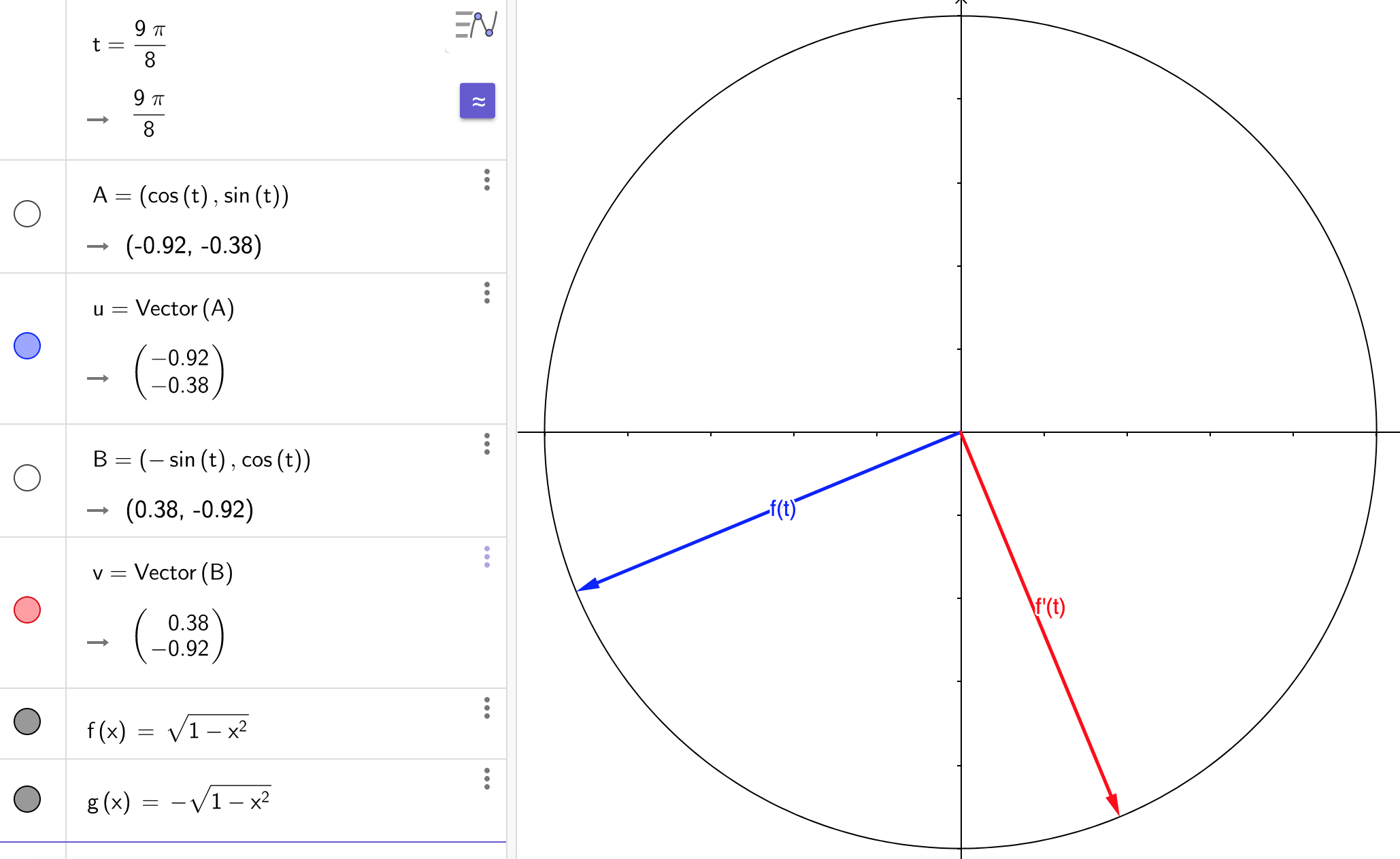
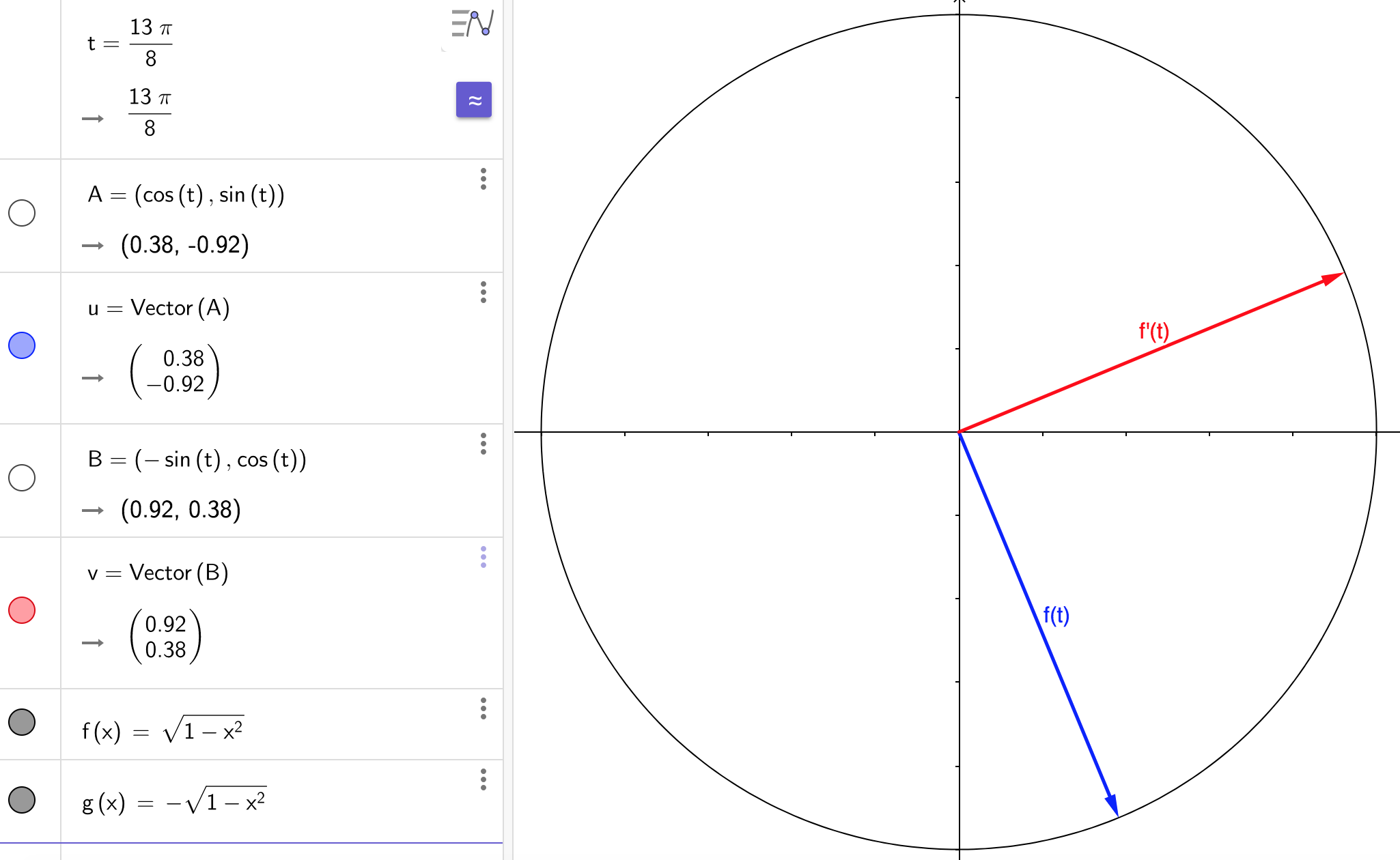
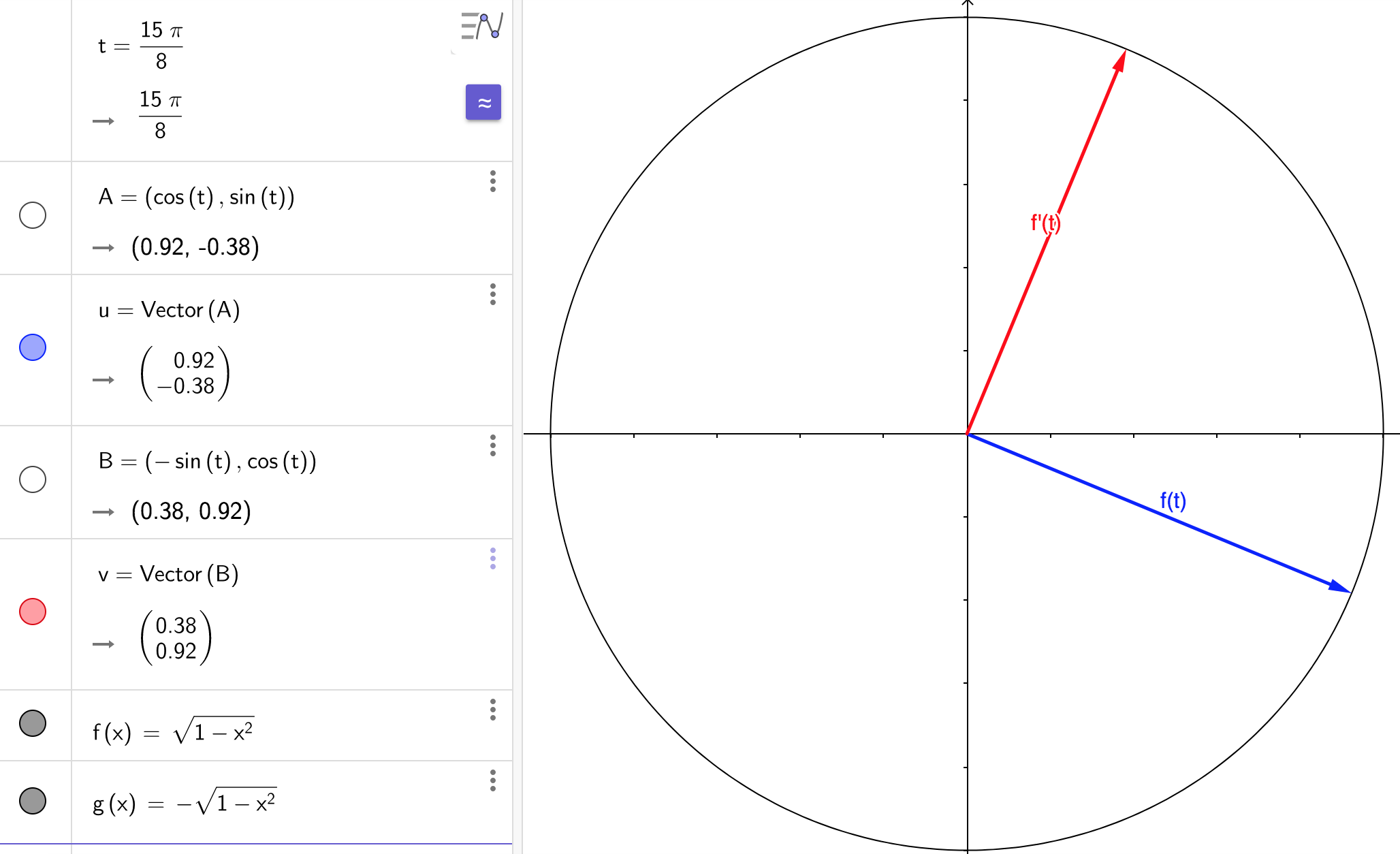
Part (c): Let $S$ be a sphere in $\mathbb{R}^n$ centered at the origin. Then every point on $S$ is equidistant to the origin. Let the distance to the origin be $c$. Let $C$ be a curve lying on $S$. Then every point $s$ on $C$ has $\dnorm{s}=c$. I cannot prove this yet, but I think $C$ can be parametered by a surjective, differentiable function $f:\mathbb{R}\mapsto C$. That is, for every point $s\in C$, there exists $t\in\mathbb{R}$ such that $f(t)=s$. Then $f’(t)\in\mathbb{R}^n$ is the tangent vector. Let’s look at an example in $\mathbb{R}^2$.
Define $f(t)\equiv(\cos{t},\sin{t})$. Then for every $t\in\mathbb{R}$, we have
$$ \dnorm{f(t)}=\dnorm{(\cos{t},\sin{t})}=\sqrt{\cos^2{t}+\sin^2{t}}=1 $$
Then the tangent vector is $f’(t)=(\cos’{t},\sin’{t})=(-\sin{t},\cos{t})$. Part (b) implies that $f(t)$ and $f’(t)$ are orthogonal. Let’s check:
$$\begin{align*} \innprdbg{f'(t)}{f(t)} &= \innprdbg{(-\sin{t},\cos{t})}{(\cos{t},\sin{t})} \\ &= -\sin{t}\cos{t}+\cos{t}\sin{t} \\ &= -\sin{t}\cos{t}+\sin{t}\cos{t} \\ &= 0 \end{align*}$$
And let’s see some graphs of these perpendicular vectors:
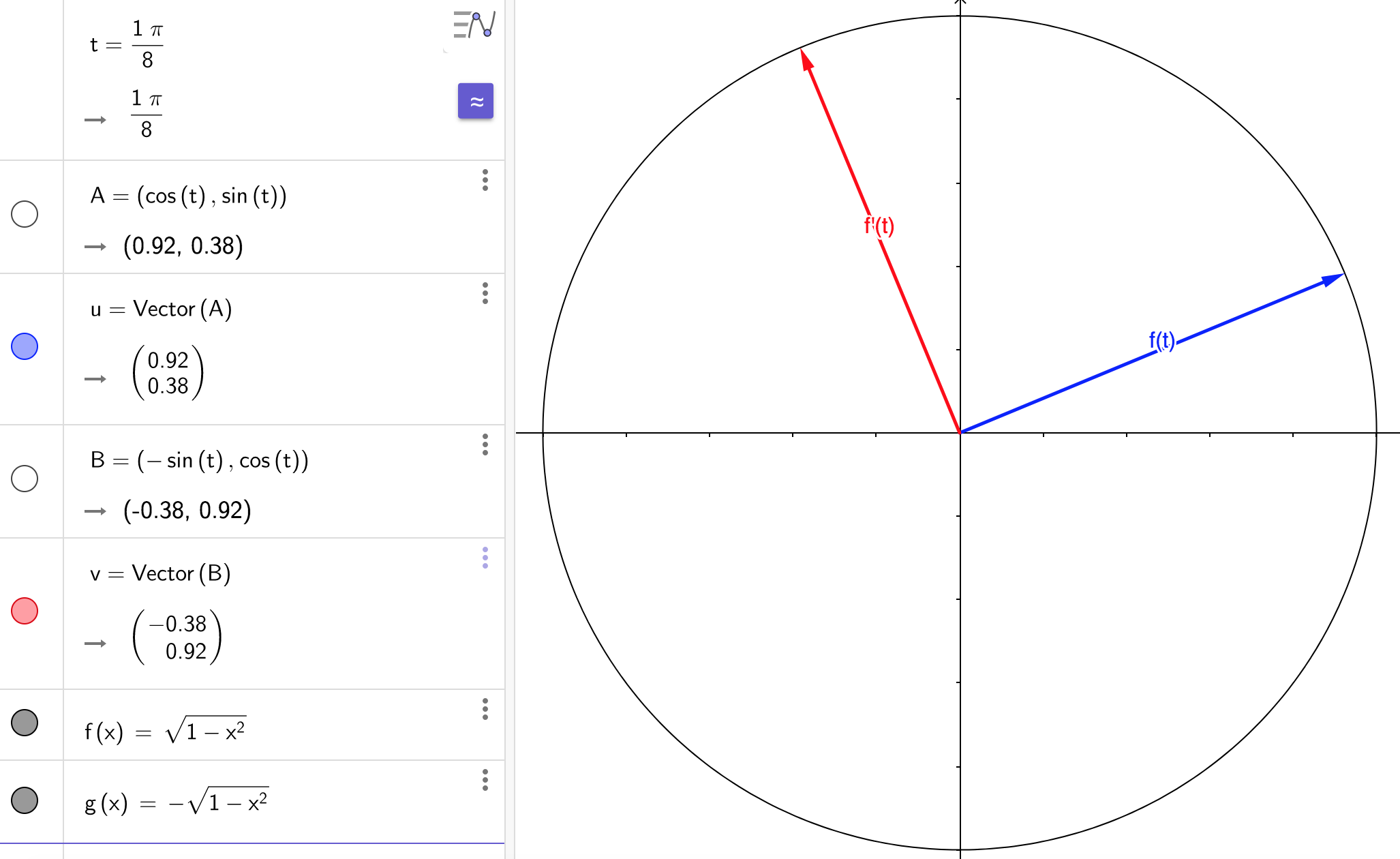
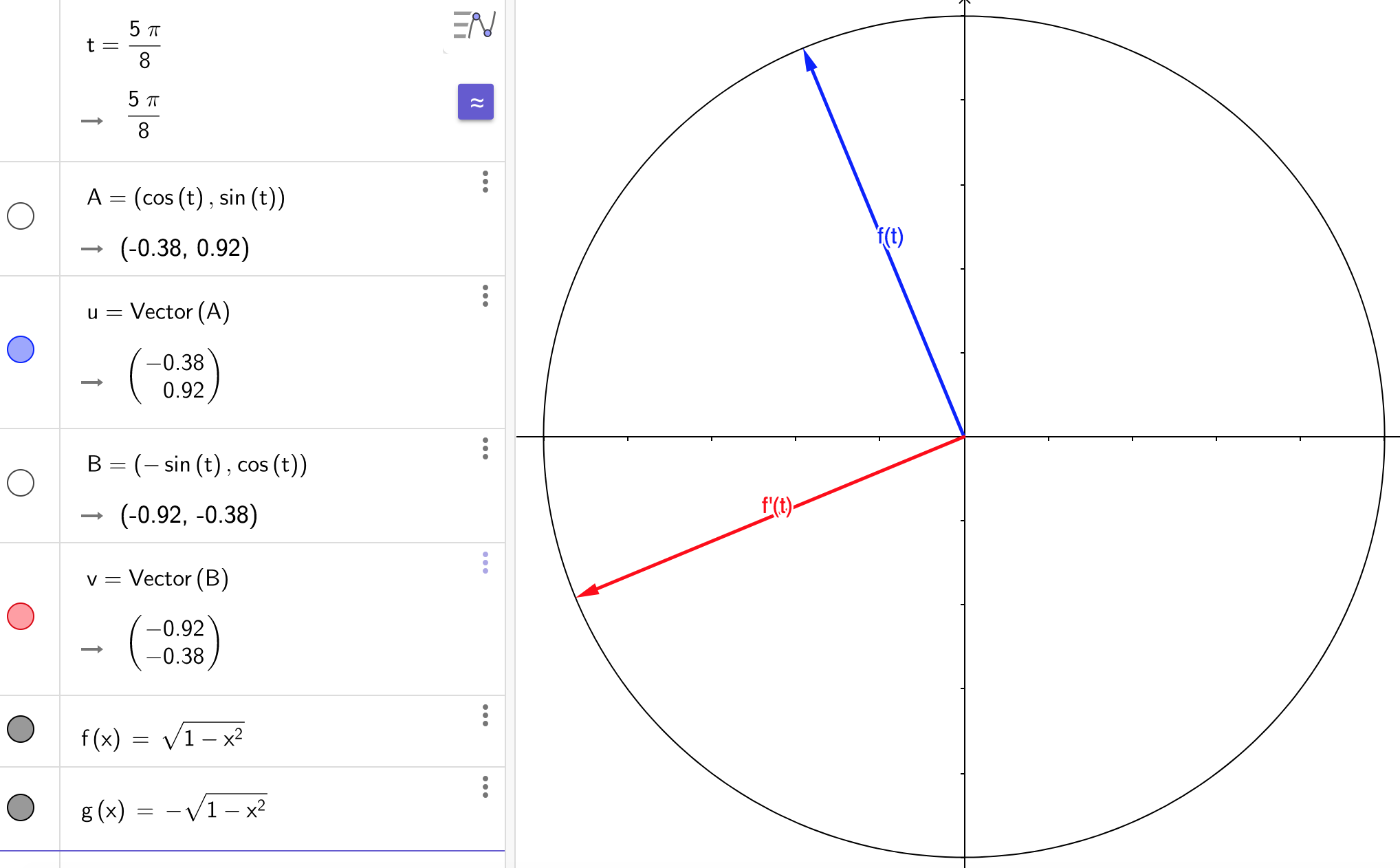
(27) Suppose $u,v,w\in V$. Then
$$ \dnorm{w-\frac12(u+v)}^2 = \frac{\dnorm{w-u}^2+\dnorm{w-v}^2}{2}-\frac{\dnorm{u-v}^2}{4} $$
Proof Define
$$ a\equiv\frac12w-\frac12u\in V \quad\quad\quad\quad b\equiv\frac12w-\frac12v\in V $$
Then
$$\begin{align*} \dnorm{w-\frac12(u+v)}^2 &= \dnorm{\frac12w+\frac12w-\frac12u-\frac12v}^2 \\ &= \dnorm{a+b}^2 \\ &= 2\dnorm{a}^2+2\dnorm{b}^2-\dnorm{a-b}^2 \\ &= 2\dnorm{\frac12w-\frac12u}^2+2\dnorm{\frac12w-\frac12v}^2-\dnorm{\frac12v-\frac12u}^2 \\ &= 2\normw{\frac12}^2\dnorm{w-u}^2+2\normw{\frac12}^2\dnorm{w-v}^2-\normw{\frac12}^2\dnorm{v-u}^2 \\ &= \frac{\dnorm{w-u}^2+\dnorm{w-v}^2}{2}-\frac{\dnorm{v-u}^2}{4} \\ &= \frac{\dnorm{w-u}^2+\dnorm{w-v}^2}{2}-\frac{\dnorm{u-v}^2}{4} \\ \end{align*}$$
where the last equality follows from
$$ \dnorm{u-v}=\dnorm{-1\cdot(v-u)}=\norm{-1}\dnorm{v-u}=\dnorm{v-u} $$
$\blacksquare$
(28) Suppose $C$ is a subset of $V$ with the property that $u,v\in C$ implies $\frac12(u+v)\in C$. Let $w\in V$. Then there is at most one point in $C$ that is closest to $w$. In other words, there is at most one $u\in C$ such that
$$ \dnorm{w-u}\leq\dnorm{w-v}\quad\text{for all }v\in C $$
Hint: Use the previous exercise.
Proof Suppose $u,t\in C$ with $u\neq t$ both satisfy
$$ \dnorm{w-u}\leq\dnorm{w-v}\quad\text{for all }v\in C \\ \dnorm{w-t}\leq\dnorm{w-v}\quad\text{for all }v\in C $$
Hence
$$ \dnorm{w-u}\leq\dnorm{w-t} \quad\quad\text{and}\quad\quad \dnorm{w-t}\leq\dnorm{w-u} $$
Hence $\dnorm{w-u}=\dnorm{w-t}$. Exercise 6.A.27 gives
$$\begin{align*} \dnorm{w-\frac12(u+t)}^2 &= \frac{\dnorm{w-u}^2+\dnorm{w-t}^2}{2}-\frac{\dnorm{u-t}^2}{4} \\ &= \frac{\dnorm{w-u}^2+\dnorm{w-u}^2}{2}-\frac{\dnorm{u-t}^2}{4} \\ &= \frac{2\dnorm{w-u}^2}{2}-\frac{\dnorm{u-t}^2}{4} \\ &= \dnorm{w-u}^2-\frac{\dnorm{u-t}^2}{4} \\ &< \dnorm{w-u}^2 \end{align*}$$
But $\frac12(u+t)\in C$ by definition. So it must be that $\dnorm{w-u}^2\leq\dnorm{w-\frac12(u+t)}^2$. This contradicts the above inequality. $\blacksquare$
Exercises 6.B
(1)
(a) Suppose $\theta\in\mathbb{R}$. Then $(\cos{\theta},\sin{\theta})$, $(-\sin{\theta},\cos{\theta})$, and $(\cos{\theta},\sin{\theta})$, $(\sin{\theta},-\cos{\theta})$ are orthonormal bases of $\mathbb{R}^2$.
(b) Show that each orthonormal basis of $\mathbb{R}^2$ is of the form given by one of the two possibilities of part (a).
Proof We have
$$\begin{align*} &\innprdbg{(\cos{\theta},\sin{\theta})}{(\cos{\theta},\sin{\theta})} = \cos^2{\theta}+\sin^2{\theta}=1 \\ &\innprdbg{(-\sin{\theta},\cos{\theta})}{(-\sin{\theta},\cos{\theta})} = (-1)^2\sin^2{\theta}+\cos^2{\theta}=1 \\ &\innprdbg{(\cos{\theta},\sin{\theta})}{(-\sin{\theta},\cos{\theta})} = -\cos{\theta}\sin{\theta}+\sin{\theta}\cos{\theta}=0 \end{align*}$$
Hence $(\cos{\theta},\sin{\theta})$, $(-\sin{\theta},\cos{\theta})$ is an orthonormal list in $\mathbb{R}^2$ and hence is a basis of $\mathbb{R}^2$ (by 6.28).
Similarly
$$\begin{align*} &\innprdbg{(\sin{\theta},-\cos{\theta})}{(\sin{\theta},-\cos{\theta})} = \sin^2{\theta}+(-1)^2\cos^2{\theta}=1 \\ &\innprdbg{(\cos{\theta},\sin{\theta})}{(\sin{\theta},-\cos{\theta})} = \cos{\theta}\sin{\theta}-\sin{\theta}\cos{\theta}=0 \end{align*}$$
Hence $(\cos{\theta},\sin{\theta})$, $(\sin{\theta},-\cos{\theta})$ is an orthonormal list in $\mathbb{R}^2$ and hence is a basis of $\mathbb{R}^2$ (by 6.28).
Let $f_1,f_2$ be an orthonormal basis of $\mathbb{R}^2$ and let $e_1,e_2$ be the standard basis of $\mathbb{R}^2$. Note that $e_1,e_2$ is orthonormal. Hence proposition 6.30 implies
$$\begin{align*} f_1=\innprd{f_1}{e_1}e_1+\innprd{f_1}{e_2}e_2 \tag{6.B.1.1} \\ f_2=\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2 \tag{6.B.1.2} \end{align*}$$
Then
$$\begin{align*} 1 &= \innprd{f_1}{f_1} \\ &= \innprdbg{f_1}{\innprd{f_1}{e_1}e_1+\innprd{f_1}{e_2}e_2} \\ &= \innprdbg{f_1}{\innprd{f_1}{e_1}e_1}+\innprdbg{f_1}{\innprd{f_1}{e_2}e_2} \\ &= \overline{\innprd{f_1}{e_1}}\innprdbg{f_1}{e_1}+\overline{\innprd{f_1}{e_2}}\innprdbg{f_1}{e_2} \\ &= \innprd{f_1}{e_1}\innprdbg{f_1}{e_1}+\innprd{f_1}{e_2}\innprdbg{f_1}{e_2} \\ &= \innprd{f_1}{e_1}^2+\innprd{f_1}{e_2}^2\tag{6.B.1.3} \end{align*}$$
Also note that Cauchy-Schwarz gives
$$ \normw{\innprd{f_1}{e_1}}\leq\dnorm{f_1}\dnorm{e_1}=1 $$
Since the cosine function is surjective from $[0,\pi]$ to $[-1,1]$, then there exists $\phi\in[0,\pi]$ such that $\innprd{f_1}{e_1}=\cos{\phi}$. Hence 6.B.1.3 gives
$$ \innprd{f_1}{e_2}^2=1-\innprd{f_1}{e_1}^2=1-\cos^2{\phi} $$
Hence $\innprd{f_1}{e_2}=\pm\sin{\phi}$. Recall that the sine function is odd. Hence $\innprd{f_1}{e_2}=\sin{\phi}$ or $\innprd{f_1}{e_2}=-\sin{\phi}=\sin{(-\phi)}$. Then define
$$ \theta\equiv\begin{cases}\phi&\text{if }\innprd{f_1}{e_2}=\sin{\phi}\\-\phi&\text{if }\innprd{f_1}{e_2}=\sin{(-\phi)}\end{cases} $$
so that $\innprd{f_1}{e_2}=\sin{\theta}$. Also recall that the cosine function is even. Hence
$$ \innprd{f_1}{e_1}=\cos{\phi}=\cos{(-\phi)}=\cos{\theta} $$
Hence 6.B.1.1 becomes
$$\begin{align*} f_1 &=\innprd{f_1}{e_1}e_1+\innprd{f_1}{e_2}e_2 \\ &= (\cos{\theta})e_1+(\sin{\theta})e_2 \\ &= (\cos{\theta},\sin{\theta}) \tag{6.B.1.4} \end{align*}$$
and
$$\begin{align*} 0 &= \innprd{f_1}{f_2} \\ &= \innprdbg{(\cos{\theta})e_1+(\sin{\theta})e_2}{f_2} \\ &= \innprdbg{(\cos{\theta})e_1}{f_2}+\innprdbg{(\sin{\theta})e_2}{f_2} \\ &= \cos{\theta}\innprd{e_1}{f_2}+\sin{\theta}\innprd{e_2}{f_2} \\ &= \cos{\theta}\innprd{f_2}{e_1}+\sin{\theta}\innprd{f_2}{e_2} \end{align*}$$
Notice that for any $\beta\in\mathbb{R}$, a solution to the above is $\innprd{f_2}{e_1}=-\beta\sin{\theta}$ and $\innprd{f_2}{e_2}=\beta\cos{\theta}$. Also note that
$$\begin{align*} 1 &= \dnorm{f_2}^2 \\ &= \innprd{f_2}{f_2} \\ &= \innprdbg{\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2}{\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2} \\ &= \innprdbg{\innprd{f_2}{e_1}e_1}{\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2}+\innprdbg{\innprd{f_2}{e_2}e_2}{\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2} \\ &= \innprdbg{\innprd{f_2}{e_1}e_1}{\innprd{f_2}{e_1}e_1}+\innprdbg{\innprd{f_2}{e_1}e_1}{\innprd{f_2}{e_2}e_2}+\innprdbg{\innprd{f_2}{e_2}e_2}{\innprd{f_2}{e_1}e_1}+\innprdbg{\innprd{f_2}{e_2}e_2}{\innprd{f_2}{e_2}e_2} \\ &= \innprd{f_2}{e_1}^2\innprdbg{e_1}{e_1}+\innprd{f_2}{e_1}\innprd{f_2}{e_2}\innprdbg{e_1}{e_2}+\innprd{f_2}{e_2}\innprd{f_2}{e_1}\innprdbg{e_2}{e_1}+\innprd{f_2}{e_2}^2\innprdbg{e_2}{e_2} \\ &= \innprd{f_2}{e_1}^2\cdot1+\innprd{f_2}{e_1}\innprd{f_2}{e_2}\cdot0+\innprd{f_2}{e_2}\innprd{f_2}{e_1}\cdot0+\innprd{f_2}{e_2}^2\cdot1 \\ &= \innprd{f_2}{e_1}^2+\innprd{f_2}{e_2}^2 \\ &= \prn{-\beta\sin{\theta}}^2+\prn{\beta\cos{\theta}}^2 \\ &= \beta^2\sin^2{\theta}+\beta^2\cos^2{\theta} \\ &= \beta^2\prn{\sin^2{\theta}+\cos^2{\theta}} \\ &= \beta^2 \end{align*}$$
Instead of using the inner product properties to compute this, we could use the simpler dot product since we’re working in $\mathbb{R}^n$:
$$\begin{align*} 1 &= \dnorm{f_2}^2 \\ &= \dnorm{\innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2}^2 \\ &= \dnorm{\prn{\innprd{f_2}{e_1},\innprd{f_2}{e_2}}}^2 \\ &= \innprd{f_2}{e_1}^2+\innprd{f_2}{e_2}^2 \\ &= \prn{-\beta\sin{\theta}}^2+\prn{\beta\cos{\theta}}^2 \\ &= \beta^2\sin^2{\theta}+\beta^2\cos^2{\theta} \\ &= \beta^2\prn{\sin^2{\theta}+\cos^2{\theta}} \\ &= \beta^2 \end{align*}$$
Hence $\beta=\pm1$ and 6.B.1.2 becomes
$$\begin{align*} f_2 &= \innprd{f_2}{e_1}e_1+\innprd{f_2}{e_2}e_2 \\ &= -\beta(\sin{\theta})e_1+\beta(\cos{\theta})e_2 \\ &= \beta\prn{-(\sin{\theta})e_1+(\cos{\theta})e_2} \\ &= \pm1\cdot\prn{-(\sin{\theta})e_1+(\cos{\theta})e_2} \\ &= \pm1\cdot(-\sin{\theta},\cos{\theta}) \tag{6.B.1.5} \end{align*}$$
Succintly, 6.B.1.4 and 6.B.1.5 are
$$\begin{align*} &f_1 = (\cos{\theta},\sin{\theta}) \\ &f_2 = \pm1\cdot(-\sin{\theta},\cos{\theta}) \end{align*}$$
Since $f_1$ and $f_2$ were arbitrary, then every orthonormal basis of $\mathbb{R}^2$ is of the form given by one of the two possibilities of part (a). $\blacksquare$
(2) Suppose $e_1,\dots,e_m$ is an orthonormal list of vectors in $V$. Let $v\in V$. Then
$$ \dnorm{v}^2=\sum_{k=1}^m\norm{\innprd{v}{e_k}}^2 $$
if and only if $v\in\text{span}(e_1,\dots,e_m)$.
Proof Suppose $v\in\text{span}(e_1,\dots,e_m)$. Since $e_1,\dots,e_m$ is linearly independent (by 6.26), then it’s a basis of $\text{span}(e_1,\dots,e_m)$ (by 2.27). Hence $e_1,\dots,e_m$ is an orthonormal basis of $\text{span}(e_1,\dots,e_m)$. Then 6.30 gives $\dnorm{v}^2=\sum_k^m\norm{\innprd{v}{e_k}}^2$.
Suppose $\dnorm{v}^2=\sum_k^m\norm{\innprd{v}{e_k}}^2$. Define
$$ u\equiv v-\sum_{k=1}^m\innprd{v}{e_k}e_k $$
Note that
$$\begin{align*} \innprdBg{u}{\sum_{k=1}^m\innprd{v}{e_k}e_k} &= \innprdBg{v-\sum_{j=1}^m\innprd{v}{e_j}e_j}{\sum_{k=1}^m\innprd{v}{e_k}e_k} \\ &= \innprdBg{v}{\sum_{k=1}^m\innprd{v}{e_j}e_j}-\innprdBg{\sum_{j=1}^m\innprd{v}{e_j}e_j}{\sum_{k=1}^m\innprd{v}{e_k}e_k} \\ &= \sum_{j=1}^m\innprdbg{v}{\innprd{v}{e_j}e_j}-\sum_{j=1}^m\innprdBg{\innprd{v}{e_j}e_j}{\sum_{k=1}^m\innprd{v}{e_k}e_k} \\ &= \sum_{j=1}^m\overline{\innprd{v}{e_j}}\innprd{v}{e_j}-\sum_{j=1}^m\sum_{k=1}^m\innprdbg{\innprd{v}{e_j}e_j}{\innprd{v}{e_k}e_k} \\ &= \sum_{j=1}^m\norm{\innprd{v}{e_j}}^2-\sum_{j=1}^m\sum_{k=1}^m\innprd{v}{e_j}\overline{\innprd{v}{e_k}}\innprd{e_j}{e_k} \\ &= \sum_{j=1}^m\norm{\innprd{v}{e_j}}^2-\sum_{j=1}^m\sum_{k=1}^m\innprd{v}{e_j}\overline{\innprd{v}{e_k}}\mathbb{1}_{j=k} \\ &= \sum_{j=1}^m\norm{\innprd{v}{e_j}}^2-\sum_{j=1}^m\innprd{v}{e_j}\overline{\innprd{v}{e_j}} \\ &= \sum_{j=1}^m\norm{\innprd{v}{e_j}}^2-\sum_{j=1}^m\norm{\innprd{v}{e_j}}^2 \\ &= 0 \end{align*}$$
A simpler way to do the above computation is to recognise that $\sum_k^m\innprd{v}{e_k}e_k$ is an orthonormal linear combination and use 6.25:
$$ \innprdBg{\sum_{j=1}^m\innprd{v}{e_j}e_j}{\sum_{k=1}^m\innprd{v}{e_k}e_k} = \dnorm{\sum_{j=1}^m\innprd{v}{e_j}e_j}^2=\sum_{j=1}^m\normw{\innprd{v}{e_j}}^2 $$
So $u$ and $\sum_{k}^m\innprd{v}{e_k}e_k$ are orthogonal and the Pythagorean Theorem (6.13) gives
$$\begin{align*} \dnorm{v}^2 &= \dnorm{u+\sum_{k=1}^m\innprd{v}{e_k}e_k}^2 \\ &= \dnorm{u}^2+\dnorm{\sum_{k=1}^m\innprd{v}{e_k}e_k}^2 \\ &= \dnorm{u}^2+\sum_{k=1}^m\normw{\innprd{v}{e_k}}^2 \\ &= \dnorm{u}^2+\dnorm{v}^2 \\ \end{align*}$$
Hence $\dnorm{u}=0$ and hence $u=0$ (by definiteness). Hence $v=\sum_k^m\innprd{v}{e_k}e_k\in\text{span}(e_1,\dots,e_m)$. $\blacksquare$
(3) Suppose $T\in\lnmpsb(\mathbb{R}^3)$ has an upper-triangular matrix with respect to the basis $(1,0,0),(1,1,1),(1,1,2)$. Find an orthonormal basis of $\mathbb{R}^3$ (use the usual inner product on $\mathbb{R}^3$) with respect to which $T$ has an upper-triangular matrix.
Solution Define
$$\begin{align*} &v_1\equiv(1,0,0) \\ &v_2\equiv(1,1,1) \\ &v_3\equiv(1,1,2) \end{align*}$$
We perform Gram-Schmidt on $v_1,v_2,v_3$:
$$ e_1=\frac{v_1}{\dnorm{v_1}}=\frac{v_1}{\sqrt{1^2+0^2+0^2}}=v_1 $$
Note that
$$\begin{align*} v_2-\innprd{v_2}{e_1}e_1 &= v_2-(1,1,1)\cdot(1,0,0)v_1 \\ &= (1,1,1)-1\cdot(1,0,0) \\ &= (0,1,1) \end{align*}$$
So
$$ e_2 = \frac{v_2-\innprd{v_2}{e_1}e_1}{\dnorm{v_2-\innprd{v_2}{e_1}e_1}} = \frac{(0,1,1)}{\sqrt2}=\Big(0,\frac1{\sqrt2},\frac1{\sqrt2}\Big) $$
Note that
$$\begin{align*} v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2 &= v_3-(1,1,2)\cdot(1,0,0)e_1-(1,1,2)\cdot\Big(0,\frac1{\sqrt2},\frac1{\sqrt2}\Big)e_2 \\ &= v_3-1\cdot e_1-\Big(\frac1{\sqrt2}+\frac2{\sqrt2}\Big)e_2 \\ &= v_3-v_1-\frac3{\sqrt2}e_2 \\ &= (0,1,2)-\Big(0,\frac32,\frac32\Big) \\ &= \Big(0,-\frac12,\frac12\Big) \end{align*}$$
So
$$\begin{align*} e_3 &= \frac{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}{\dnorm{v_3-\innprd{v_3}{e_1}e_1-\innprd{v_3}{e_2}e_2}} \\ &= \frac{\big(0,-\frac12,\frac12\big)}{\sqrt{0^2+\prn{-\frac12}^2+\prn{\frac12}^2}} \\ &= \frac{\prn{0,-\frac12,\frac12}}{\sqrt{\frac14+\frac14}} \\ &= \frac{\prn{0,-\frac12,\frac12}}{\frac1{\sqrt2}} \\ &= \sqrt{2}\Prn{0,-\frac12,\frac12} \\ &= \Prn{0,-\frac{\sqrt{2}}2,\frac{\sqrt{2}}2} \end{align*}$$
Since $e_1,e_2,e_3$ is linearly independent (by 6.26), then it’s a basis for $\mathbb{R}^3$. Since $T$ has an upper-triangular matrix with respect to $v_1,v_2,v_3$, then $\mathbb{R}^3=\text{span}(v_1,v_2,v_3)$ is invariant under $T$ (by 5.26). Hence $\text{span}(e_1,e_2,e_3)=\mathbb{R}^3$ is invariant under $T$. Hence the matrix of $T$ with respect to $e_1,e_2,e_3$ is upper-triangular (by 5.26). $\blacksquare$
(4) Suppose $n$ is a positive integer. Then
$$ L\equiv\frac{1}{\sqrt{2\pi}},\frac{\cos{x}}{\sqrt{\pi}},\frac{\cos{2x}}{\sqrt{\pi}},\dots,\frac{\cos{nx}}{\sqrt{\pi}}, \frac{\sin{x}}{\sqrt{\pi}},\frac{\sin{2x}}{\sqrt{\pi}},\dots,\frac{\sin{nx}}{\sqrt{\pi}} $$
is an orthonormal list of vectors in $\mathscr{C}[-\pi,\pi]$, the vector space of continuous real-valued functions on $[-\pi,\pi]$ with inner product
$$ \innprd{f}{g}\equiv\int_{-\pi}^{\pi}f(x)g(x)dx $$
The orthonormal list above is often used for modeling periodic phenomena such as tides.
Proof Note that the function $f_{k,l}(x)\equiv\sin{(kx)}\cos{(lx)}$ is odd for all $k=1,\dots,n$ and all $l=1,\dots,n$:
$$ f_{k,l}(-x)=\sin{(-kx)}\cos{(-lx)}=-\sin{(kx)}\cos{(lx)}=-f_{k,l}(x) $$
Hence, for all $k=1,\dots,n$ and all $l=1,\dots,n$, we have
$$ \innprdBg{\frac{\sin{(kx)}}{\sqrt{\pi}}}{\frac{\cos{(lx)}}{\sqrt{\pi}}}=\int_{-\pi}^{\pi}\frac{\sin{(kx)}}{\sqrt{\pi}}\frac{\cos{(lx)}}{\sqrt{\pi}}dx=\frac1\pi\int_{-\pi}^{\pi}f_{k,l}(x)dx=0 \tag{6.B.4.1} $$
since we’re integrating an odd function over a symmetric domain. Similarly, since the function $\sin{(kx)}$ is odd, then
$$ \innprdBg{\frac{\sin{(kx)}}{\sqrt{\pi}}}{\frac{1(x)}{\sqrt{2\pi}}}=\int_{-\pi}^{\pi}\frac{\sin{(kx)}}{\sqrt{\pi}}\frac{1}{\sqrt{2\pi}}dx=\frac1{\pi\sqrt2}\int_{-\pi}^{\pi}\sin{(kx)}dx=0 \tag{6.B.4.2} $$
Also note that for any nonzero integer $k$, we have
$$\align{ \innprd{\cos{(kx)}}{1(x)} &= \int_{-\pi}^{\pi}\cos{(kx)}1(x)dx \\ &= \int_{-\pi}^{\pi}\cos{(kx)}dx \\ &= 2\int_{0}^{\pi}\cos{(kx)}dx\tag{cosine is even} \\ &= 2\int_{0}^{k\pi}\cos{(u)}\frac{du}{k} \\ &= \frac2k\int_{0}^{k\pi}\cos{(u)}du \\ &= \frac2k\Prn{\sin{u}\eval0{k\pi}} \\ &= 0\tag{6.B.4.3} }$$
where we performed the substitution
$$ u=k x \quad\quad du=k dx \quad\quad dx=\frac{du}{k} \quad\quad u_0=k x_0=k\cdot0=0 \quad\quad u_1=k x_1=k\pi $$
Hence
$$ \innprdBg{\frac{\cos{(kx)}}{\sqrt{\pi}}}{\frac{1(x)}{\sqrt{2\pi}}} = \frac1{\sqrt{\pi}}\frac1{\sqrt{2\pi}}\innprd{\cos{(kx)}}{1(x)}=0 \tag{6.B.4.4} $$
Recall the trig identities
$$ \cos{(\theta)}\cos{(\phi)}=\frac{\cos{(\theta-\phi)}+\cos{(\theta+\phi)}}2 $$
$$ \sin{(\theta)}\sin{(\mathscr{\phi})}=\frac{\cos{(\theta-\phi)}-\cos{(\theta+\phi)}}2 $$
Then for any integers $j$ and $k$, we have
$$ \cos{(jx)}\cos{(kx)}=\frac{\cos{(jx-kx)}+\cos{(jx+kx)}}2=\frac{\cos{\prn{[j-k]x}}+\cos{\prn{[j+k]x}}}2 $$
Hence for $j\neq k$, the integers $j-k$ and $j+k$ are nonzero and we have
$$\align{ \innprd{\cos{(jx)}}{\cos{(kx)}} &= \int_{-\pi}^{\pi}\cos{(jx)}\cos{(kx)}dx \\ &= \int_{-\pi}^{\pi}\frac{\cos{\prn{[j-k]x}}+\cos{\prn{[j+k]x}}}2dx \\ &= \frac12\int_{-\pi}^{\pi}\cos{\prn{[j-k]x}}dx+\frac12\int_{-\pi}^{\pi}\cos{\prn{[j+k]x}}dx \\ &= \frac12\innprdbg{\cos{\prn{[j-k]x}}}{1(x)}+\frac12\innprdbg{\cos{\prn{[j+k]x}}}{1(x)} \\ &= \frac12\cdot0+\frac12\cdot0\tag{by 6.B.4.3} \\ &= 0 }$$
Hence for $j\neq k$, we have
$$ \innprdBg{\frac{\cos{(jx)}}{\sqrt{\pi}}}{\frac{\cos{(kx)}}{\sqrt{\pi}}} = \frac1{\sqrt{\pi}}\frac1{\sqrt{\pi}}\innprd{\cos{(jx)}}{\cos{(kx)}}=0 \tag{6.B.4.5} $$
Similarly, for any integers $j$ and $k$, we have
$$ \sin{(jx)}\sin{(kx)}=\frac{\cos{(jx-kx)}-\cos{(jx+kx)}}2=\frac{\cos{\prn{[j-k]x}}-\cos{\prn{[j+k]x}}}2 $$
Hence for $j\neq k$, the integers $j-k$ and $j+k$ are nonzero and we have
$$\align{ \innprd{\sin{(jx)}}{\sin{(kx)}} &= \int_{-\pi}^{\pi}\sin{(jx)}\sin{(kx)}dx \\ &= \int_{-\pi}^{\pi}\frac{\cos{\prn{[j-k]x}}-\cos{\prn{[j+k]x}}}2dx \\ &= \frac12\int_{-\pi}^{\pi}\cos{\prn{[j-k]x}}dx-\frac12\int_{-\pi}^{\pi}\cos{\prn{[j+k]x}}dx \\ &= \frac12\innprdbg{\cos{\prn{[j-k]x}}}{1(x)}-\frac12\innprdbg{\cos{\prn{[j+k]x}}}{1(x)} \\ &= \frac12\cdot0-\frac12\cdot0\tag{by 6.B.4.3} \\ &= 0 }$$
Hence for $j\neq k$, we have
$$ \innprdBg{\frac{\sin{(jx)}}{\sqrt{\pi}}}{\frac{\sin{(kx)}}{\sqrt{\pi}}} = \frac1{\sqrt{\pi}}\frac1{\sqrt{\pi}}\innprd{\sin{(jx)}}{\sin{(kx)}}=0 \tag{6.B.4.6} $$
Hence 6.B.4.1, 6.B.4.2, 6.B.4.4, 6.B.4.5, and 6.B.4.6 give the orthogonality of the list $L$.
Let’s check the norms:
$$ \dnorm{1}^2 = \innprd{1}{1} = \int_{-\pi}^{\pi}1(x)1(x)dx=\int_{-\pi}^{\pi}dx=x\eval{-\pi}{\pi}=\pi-(-\pi)=2\pi \tag{6.B.4.7} $$
Hence
$$ \dnorm{\frac1{\sqrt{2\pi}}}^2 = \normw{\frac1{\sqrt{2\pi}}}^2\dnorm{1}^2 =\frac1{2\pi}\cdot2\pi=1 \tag{6.B.4.8} $$
Note that for any integer $k$, we have
$$ \cos{(kx)}\cos{(kx)}=\frac{\cos{(kx-kx)}+\cos{(kx+kx)}}2=\frac{\cos{(0)}+\cos{(2kx)}}2=\frac12+\frac12\cos{(2kx)} $$
Hence for $k=1,\dots,n$, we have
$$\align{ \innprd{\cos{(kx)}}{\cos{(kx)}} &= \int_{-\pi}^{\pi}\cos{(kx)}\cos{(kx)}dx \\ &= \frac12\int_{-\pi}^{\pi}dx+\frac12\int_{-\pi}^{\pi}\cos{(2kx)}dx \\ &= \frac12\innprd{1}{1}+\frac12\innprd{\cos{(2kx)}}{1(x)} \\ &= \frac12\dnorm{1}^2+\frac12\cdot0\tag{by 6.B.4.3} \\ &= \pi\tag{by 6.B.4.7} }$$
Hence for $k=1,\dots,n$, we have
$$ \dnorm{\frac{\cos{(kx)}}{\sqrt\pi}}^2=\innprdBg{\frac{\cos{(kx)}}{\sqrt\pi}}{\frac{\cos{(kx)}}{\sqrt\pi}}=\frac1{\sqrt\pi}\frac1{\sqrt\pi}\innprd{\cos{(kx)}}{\cos{(kx)}}=\frac1\pi\cdot\pi=1 \tag{6.B.4.9} $$
Similarly, for any integer $k$, we have
$$ \sin{(kx)}\sin{(kx)}=\frac{\cos{(kx-kx)}-\cos{(kx+kx)}}2=\frac{\cos{(0)}-\cos{(2kx)}}2=\frac12-\frac12\cos{(2kx)} $$
Hence for $k=1,\dots,n$, we have
$$\align{ \innprd{\sin{(kx)}}{\sin{(kx)}} &= \int_{-\pi}^{\pi}\sin{(kx)}\sin{(kx)}dx \\ &= \frac12\int_{-\pi}^{\pi}dx-\frac12\int_{-\pi}^{\pi}\cos{(2kx)}dx \\ &= \frac12\innprd{1}{1}-\frac12\innprd{\cos{(2kx)}}{1(x)} \\ &= \frac12\dnorm{1}^2-\frac12\cdot0\tag{by 6.B.4.3} \\ &= \pi\tag{by 6.B.4.7} }$$
Hence for $k=1,\dots,n$, we have
$$ \dnorm{\frac{\sin{(kx)}}{\sqrt\pi}}^2=\innprdBg{\frac{\sin{(kx)}}{\sqrt\pi}}{\frac{\sin{(kx)}}{\sqrt\pi}}=\frac1{\sqrt\pi}\frac1{\sqrt\pi}\innprd{\sin{(kx)}}{\sin{(kx)}}=\frac1\pi\cdot\pi=1 \tag{6.B.4.10} $$
Hence 6.B.4.8, 6.B.4.9, and 6.B.4.10 give that $L$ is normalized. Hence $L$ is orthonormal. $\blacksquare$
(5) On $\polyrn{2}$, consider the inner product given by
$$ \innprd{p}{q}\equiv\int_0^1p(x)q(x)dx $$
Apply the Gram-Schmidt procedure to the basis $1,x,x^2$ to produce an orthonormal basis of $\polyrn{2}$.
Proof We have
$$ e_1\equiv\frac{1}{\dnorm{1}}=\frac{1}{\sqrt{\int_0^11(t)1(t)dt}}=\frac1{\sqrt{\int_0^1dt}}=\frac1{\sqrt{t\eval01}}=\frac11=1 $$
Next, note that
$$ x-\innprd{x}{e_1}e_1=x-\int_0^1x(t)1(t)dt\cdot1=x-\int_0^1tdt\cdot1=x-\frac12\Prn{t^2\eval01}\cdot1=x-\frac12\cdot1 $$
and
$$\align{ \dnorm{x-\innprd{x}{e_1}e_1} &= \dnorm{x-\frac12\cdot1} \\ &= \sqrt{\int_0^1\Prn{x-\frac12\cdot1}(t)\Prn{x-\frac12\cdot1}(t)dt} \\ &= \sqrt{\int_0^1\Prn{x-\frac12\cdot1}^2(t)dt} \\ &= \sqrt{\int_0^1\Prn{t-\frac12}^2dt} \\ &= \sqrt{\int_0^1\Prn{t^2-\frac12t-\frac12t+\frac14}dt} \\ &= \sqrt{\int_0^1\Prn{t^2-t+\frac14}dt} \\ &= \sqrt{\int_0^1t^2dt-\int_0^1tdt+\frac14\int_0^1dt} \\ &= \sqrt{\frac13\Prn{t^3\eval01}-\frac12\Prn{t^2\eval01}+\frac14\Prn{t\eval01}} \\ &= \sqrt{\frac13-\frac12+\frac14} \\ &= \sqrt{\frac13-\frac14} \\ &= \sqrt{\frac4{12}-\frac3{12}} \\ &= \sqrt{\frac1{12}} \\ &= \frac1{\sqrt{12}} \\ &= \frac1{\sqrt{4\cdot3}} \\ &= \frac1{2\sqrt{3}} }$$
Hence
$$ e_2\equiv\frac{x-\innprd{x}{e_1}e_1}{\dnorm{x-\innprd{x}{e_1}e_1}}=2\sqrt3\Prn{x-\frac12\cdot1}=\sqrt3(2x-1) $$
Next, note that
$$\align{ x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2 &= x^2-\int_0^1x^2(t)1(t)dt\cdot1 \\ &- \int_0^1x^2(t)2\sqrt3\Prn{x-\frac12\cdot1}(t)dt\cdot2\sqrt3\Prn{x-\frac12\cdot1} \\ &= x^2-\int_0^1t^2dt\cdot1 \\ &- 2\sqrt3\int_0^1t^2\Prn{t-\frac12}dt\cdot2\sqrt3\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\Prn{t^3\eval01}\cdot1 \\ &- \Cbr{\int_0^1\Prn{t^3-\frac12t^2}dt}\cdot4\cdot3\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1 \\ &- \Cbr{\int_0^1t^3dt-\frac12\int_0^1t^2dt}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\Cbr{\frac14\Prn{t^4\eval01}-\frac12\frac13\Prn{t^3\eval01}}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\Cbr{\frac14-\frac12\frac13}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\Cbr{\frac14-\frac16}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\Cbr{\frac3{12}-\frac2{12}}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\frac1{12}\cdot12\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-\Prn{x-\frac12\cdot1} \\ &= x^2-\frac13\cdot1-x+\frac12\cdot1 \\ &= x^2-x+\frac12\cdot1-\frac13\cdot1 \\ &= x^2-x+\Prn{\frac12-\frac13}\cdot1 \\ &= x^2-x+\Prn{\frac36-\frac26}\cdot1 \\ &= x^2-x+\frac16\cdot1 \\ }$$
and
$$\align{ \dnorm{x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2} &= \dnorm{x^2-x+\frac16\cdot1} \\ &= \sqrt{\int_0^1\Prn{x^2-x+\frac16\cdot1}(t)\Prn{x^2-x+\frac16\cdot1}(t)dt} \\ &= \sqrt{\int_0^1\Prn{x^2-x+\frac16\cdot1}^2(t)dt} \\ &= \sqrt{\int_0^1\Prn{t^2-t+\frac16}^2dt} \\ &= \sqrt{\int_0^1\Prn{t^4-t^3+\frac16t^2-t^3+t^2-\frac16t+\frac16t^2-\frac16t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1\Prn{t^4-2t^3+\frac16t^2+t^2-\frac16t+\frac16t^2-\frac16t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1\Prn{t^4-2t^3+\Prn{\frac16+1+\frac16}t^2-\frac16t-\frac16t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1\Prn{t^4-2t^3+\frac86t^2-\frac16t-\frac16t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1\Prn{t^4-2t^3+\frac86t^2-\Prn{\frac16+\frac16}t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1\Prn{t^4-2t^3+\frac86t^2-\frac13t+\frac1{36}}dt} \\ &= \sqrt{\int_0^1t^4dt-2\int_0^1t^3dt+\frac86\int_0^1t^2dt-\frac13\int_0^1tdt+\frac1{36}\int_0^1dt} \\ &= \sqrt{\frac15\Prn{t^5\eval01}-2\cdot\frac14\Prn{t^4\eval01}+\frac86\frac13\Prn{t^3\eval01}-\frac13\frac12\Prn{t^2\eval01}+\frac1{36}\Prn{t\eval01}} \\ &= \sqrt{\frac15-2\cdot\frac14+\frac86\frac13-\frac13\frac12+\frac1{36}} \\ &= \sqrt{\frac15-\frac12+\frac8{18}-\frac16+\frac1{36}} \\ &= \sqrt{\frac15-\frac9{18}+\frac8{18}-\frac3{18}+\frac1{36}} \\ &= \sqrt{\frac15+\frac{-9+8-3}{18}+\frac1{36}} \\ &= \sqrt{\frac15-\frac{4}{18}+\frac1{36}} \\ &= \sqrt{\frac15-\frac{8}{36}+\frac1{36}} \\ &= \sqrt{\frac15+\frac{-8+1}{36}} \\ &= \sqrt{\frac15-\frac{7}{36}} \\ &= \sqrt{\frac15\frac{36}{36}-\frac{7}{36}\frac55} \\ &= \sqrt{\frac{36}{36\cdot5}-\frac{7\cdot5}{36\cdot5}} \\ &= \sqrt{\frac{36-35}{36\cdot5}} \\ &= \sqrt{\frac{1}{36\cdot5}} \\ &= \frac1{\sqrt{36\cdot5}} \\ &= \frac1{\sqrt{36}\sqrt{5}} \\ &= \frac1{6\sqrt{5}} \\ }$$
Hence
$$\align{ e_3 &\equiv \frac{x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2}{\dnorm{x^2-\innprd{x^2}{e_1}e_1-\innprd{x^2}{e_2}e_2}} \\ &= \frac{x^2-x+\frac16\cdot1}{\frac1{6\sqrt{5}}} \\ &= 6\sqrt{5}\Prn{x^2-x+\frac16\cdot1} \\ &= \sqrt5(6x^2-6x+1) \\ }$$
In summary:
$$\align{ &e_1\equiv 1 \\ &e_2\equiv \sqrt3(2x-1) \\ &e_3\equiv \sqrt5(6x^2-6x+1) }$$
$\blacksquare$
(6) Find an orthonormal basis of $\polyrn{2}$ (with inner product as in Exercise 5) such that the differentiation operator (the operator that takes $p$ to $p’$) on $\polyrn{2}$ has an upper-triangular matrix with respect to this basis.
Proof Let $D\in\operb{\polyrn{2}}$ denote the differentiation operator defined by $Dp\equiv p’$. First we will show that the matrix of $D$ with respect to the standard basis $1,x,x^2$ of $\polyrn{2}$ is upper-triangular.
The entries $A_{j,k}$ of $\mtrxof{D}$ for the standard basis are defined by
$$\align{ & D1 =0 = 0\cdot 1+0\cdot x+0\cdot x^2 = A_{1,1}1+A_{2,1}x+A_{3,1}x^2 \\ & Dx =1 = 1\cdot1+0\cdot x+0\cdot x^2 = A_{1,2}1+A_{2,2}x+A_{3,2}x^2 \\ & Dx^2 =2x = 0\cdot 1+2\cdot x+0\cdot x^2 = A_{1,3}1+A_{2,3}x+A_{3,3}x^2 }$$
Hence
$$ \mtrxofb{D,(1,x,x^2)}\equiv\begin{bmatrix}A_{1,1}&A_{1,2}&A_{1,3}\\A_{2,1}&A_{2,2}&A_{2,3}\\A_{3,1}&A_{3,2}&A_{3,3}\end{bmatrix} =\begin{bmatrix}0&1&0\\0&0&2\\0&0&0\\\end{bmatrix} $$
But $1,x,x^2$ is not an orthonormal basis. For example
$$ \innprd{1}{x}=\int_0^11(t)x(t)dt=\int_0^1tdt=\frac12\Prn{t^2\eval01}=\frac12\neq0 $$
However, in the proof of 6.37, we see that the matrix of $D$ will be upper-triangular for the orthonormal basis produced by applying Gram-Schmidt to $1,x,x^2$. Let’s verify this. We computed this orthonormal basis in the previous exercise:
$$\align{ &e_1\equiv 1 \\ &e_2\equiv \sqrt3(2x-1)=2\sqrt{3}\cdot x-\sqrt{3}\cdot1 \\ &e_3\equiv \sqrt5(6x^2-6x+1)=6\sqrt{5}\cdot x^2-6\sqrt{5}\cdot x+\sqrt{5}\cdot1 }$$
Then
$$\align{ & De_1 =0 = 0\cdot 1+0\cdot x+0\cdot x^2 \\ & De_2 =2\sqrt3\cdot1 = 2\sqrt3\cdot1+0\cdot x+0\cdot x^2 \\ & De_3 =6\sqrt{5}\cdot x -6\sqrt{5}\cdot 1= -6\sqrt{5}\cdot 1+6\sqrt{5}\cdot x+0\cdot x^2 }$$
Hence
$$ \mtrxofb{D,(e_1,e_2,e_3)}\equiv\begin{bmatrix}A_{1,1}&A_{1,2}&A_{1,3}\\A_{2,1}&A_{2,2}&A_{2,3}\\A_{3,1}&A_{3,2}&A_{3,3}\end{bmatrix} =\begin{bmatrix}0&2\sqrt3&-6\sqrt{5}\\0&0&6\sqrt{5}\\0&0&0\\\end{bmatrix} $$
$\blacksquare$
(7) Find a polynomial $q\in\polyrn{2}$ such that
$$ p\Prn{\frac12}=\int_0^1p(x)q(x)dx $$
for every $p\in\polyrn{2}$.
Solution We require an orthonormal basis of $\polyrn{2}$. We computed such a basis in exercise 6.B.5:
$$\align{ &e_1\equiv 1 \\ &e_2\equiv \sqrt3(2x-1) \\ &e_3\equiv \sqrt5(6x^2-6x+1) }$$
Define a linear functional on $\polyrn{2}$ by
$$\align{ \varphi(p)\equiv p\Prn{\frac12} }$$
Since $\innprd{p}{q}\equiv\int_0^1p(t)q(t)dt$ defines an inner product on $\polyrn{2}$, then we want to find $q\in\polyrn{2}$ such that
$$ \varphi(p)=p\Prn{\frac12}=\int_0^1p(t)q(t)dt=\innprd{p}{q} $$
for every $p\in\polyrn{2}$. Formula 6.43 gives
$$ q=\varphi(e_1)e_1+\varphi(e_2)e_2+\varphi(e_3)e_3 $$
Hence
$$\align{ q(t) &= \varphi(e_1)e_1(t)+\varphi(e_2)e_2(t)+\varphi(e_3)e_3(t) \\ &= e_1\Prn{\frac12}1(t)+e_2\Prn{\frac12}\sqrt3(2x-1)(t)+e_3\Prn{\frac12}\sqrt5(6x^2-6x+1)(t) \\ &= 1\Prn{\frac12}+\sqrt3(2x-1)\Prn{\frac12}\sqrt3(2t-1)+\sqrt5(6x^2-6x+1)\Prn{\frac12}\sqrt5(6t^2-6t+1) \\ &= 1+3\Prn{2\cdot\frac12-1}(2t-1)+5\Prn{6\Prn{\frac12}^2-6\cdot\frac12+1}(6t^2-6t+1) \\ &= 1+5\Prn{6\cdot\frac14-3+1}(6t^2-6t+1) \\ &= 1+\Prn{\frac32-2}(30t^2-30t+5) \\ &= 1-\frac12(30t^2-30t+5) \\ &= 1-15t^2+15t-\frac52 \\ &= -15t^2+15t-\frac52+\frac22 \\ &= -15t^2+15t+\frac{-5+2}2 \\ &= -15t^2+15t-\frac32 \\ }$$
$\blacksquare$
(8) Find a polynomial $q\in\polyrn{2}$ such that
$$ \int_0^1p(x)(\cos\pi x)dx=\int_0^1p(x)q(x)dx $$
for every $p\in\polyrn{2}$.
Solution We require an orthonormal basis of $\polyrn{2}$. We computed such a basis in exercise 6.B.5:
$$\align{ &e_1\equiv 1 \\ &e_2\equiv \sqrt3(2x-1) \\ &e_3\equiv \sqrt5(6x^2-6x+1) }$$
Define a linear functional on $\polyrn{2}$ by
$$\align{ \varphi(p)\equiv \int_0^1p(t)(\cos\pi t)dt }$$
Since $\innprd{p}{q}\equiv\int_0^1p(t)q(t)dt$ defines an inner product on $\polyrn{2}$, then we want to find $q\in\polyrn{2}$ such that
$$ \varphi(p)=\int_0^1p(t)(\cos\pi t)dt=\int_0^1p(t)q(t)dt=\innprd{p}{q} $$
for every $p\in\polyrn{2}$. Formula 6.43 gives
$$ q=\varphi(e_1)e_1+\varphi(e_2)e_2+\varphi(e_3)e_3 $$
Let’s compute
$$ \int_0^1(\cos{\pi t})dt = \int_0^\pi(\cos{u})\frac{du}{\pi} = \frac{1}{\pi}\int_0^\pi(\cos{u})du = \frac{1}{\pi}\Prn{\sin{u}\eval0\pi} = \frac1\pi(0-0) = 0 $$
where we performed the substitution
$$ u=\pi t \quad\quad du=\pi dt \quad\quad dt=\frac{du}{\pi} \quad\quad u_0=\pi t_0=\pi\cdot0=0 \quad\quad u_1=\pi t_1=\pi\cdot1=\pi $$
Similarly
$$ \int_0^1(\sin{\pi t})dt = \int_0^\pi(\sin{u})\frac{du}{\pi} = \frac{1}{\pi}\int_0^\pi(\sin{u})du = -\frac{1}{\pi}\Prn{\cos{u}\eval0\pi} = -\frac1\pi(-1-1) =\frac2\pi $$
where we performed the same substitution as above. In the next computation, we perform this integration by parts:
$$ u=t \quad\quad du=dt \quad\quad dv=(\cos{\pi t})dt \quad\quad v=\frac1\pi\sin{\pi t} $$
$$\align{ \int_0^1t(\cos{\pi t})dt &= \Prn{uv\eval01}-\int_0^1vdu \\ &= \Prn{t\frac1\pi(\sin{\pi t})\eval01}-\int_0^1\frac1\pi(\sin{\pi t})dt \\ &= \frac1\pi\Prn{t(\sin{\pi t})\eval01}-\frac1\pi\int_0^1(\sin{\pi t})dt \\ &= \frac1\pi\sin{\pi}-\frac1\pi\frac2\pi \\ &= -\frac2{\pi^2} }$$
In the next computation, we perform this integration by parts:
$$ u=t \quad\quad du=dt \quad\quad dv=(\sin{\pi t})dt \quad\quad v=-\frac1\pi\cos{\pi t} $$
$$\align{ \int_0^1t(\sin{\pi t})dt &= \Prn{uv\eval01}-\int_0^1vdu \\ &= \Prn{-t\frac1\pi(\cos{\pi t})\eval01}-\int_0^1-\frac1\pi(\cos{\pi t})dt \\ &= -\frac1\pi\Prn{t(\cos{\pi t})\eval01}+\frac1\pi\int_0^1(\cos{\pi t})dt \\ &= -\frac1\pi\cos{\pi}+\frac1\pi\cdot0 \\ &= \frac1\pi }$$
In the next computation, we perform this integration by parts:
$$ u=t^2 \quad\quad du=2tdt \quad\quad dv=(\cos{\pi t})dt \quad\quad v=\frac1\pi\sin{\pi t} $$
$$\align{ \int_0^1t^2(\cos{\pi t})dt &= \Prn{uv\eval01}-\int_0^1vdu \\ &= \Prn{t^2\frac1\pi(\sin{\pi t})\eval01}-\int_0^1\frac1\pi(\sin{\pi t})2tdt \\ &= \frac1\pi\Prn{t^2(\sin{\pi t})\eval01}-\frac2\pi\int_0^1t(\sin{\pi t})dt \\ &= \frac1\pi\sin{\pi}-\frac2\pi\frac1\pi \\ &= -\frac2{\pi^2} }$$
Hence
$$\align{ q(t) &= \varphi(e_1)e_1(t)+\varphi(e_2)e_2(t)+\varphi(e_3)e_3(t) \\ &= \int_0^1e_1(t)(\cos\pi t)dt\cdot1(t)+\int_0^1e_2(t)(\cos\pi t)dt\cdot\sqrt3(2x-1)(t) \\ &+ \int_0^1e_3(t)(\cos\pi t)dt\cdot\sqrt5(6x^2-6x+1)(t) \\ &= \int_0^11(t)(\cos\pi t)dt+\int_0^1\sqrt3(2x-1)(t)(\cos\pi t)dt\cdot\sqrt3(2t-1) \\ &+ \int_0^1\sqrt5(6x^2-6x+1)(t)(\cos\pi t)dt\cdot\sqrt5(6t^2-6t+1) \\ &= \int_0^1(\cos\pi t)dt+\sqrt3\int_0^1(2t-1)(\cos\pi t)dt\cdot\sqrt3(2t-1) \\ &+ \sqrt5\int_0^1(6t^2-6t+1)(\cos\pi t)dt\cdot\sqrt5(6t^2-6t+1) \\ &= 3\int_0^1(2t-1)(\cos\pi t)dt\cdot(2t-1) \\ &+ 5\int_0^1(6t^2-6t+1)(\cos\pi t)dt\cdot(6t^2-6t+1) \\ &= 3\Cbr{2\int_0^1t(\cos\pi t)dt-\int_0^1(\cos\pi t)dt}\cdot(2t-1) \\ &+ 5\Cbr{6\int_0^1t^2(\cos\pi t)dt-6\int_0^1t(\cos\pi t)dt+\int_0^1(\cos\pi t)dt}\cdot(6t^2-6t+1) \\ &= 3\Cbr{2\Prn{-\frac2{\pi^2}}}\cdot(2t-1)+ 5\Cbr{6\Prn{-\frac2{\pi^2}}-6\Prn{-\frac2{\pi^2}}}\cdot(6t^2-6t+1) \\ &= -\frac{12}{\pi^2}\cdot(2t-1) }$$
$\blacksquare$
(9) What happens if the Gram-Schmidt procedure is applied to a list of vectors that is not linearly independent?
Solution Suppose $v_1,\dots,v_n$ is linearly dependent.
If $v_1=0$, then at the first step of applying Gram-Schmidt to $v_1,\dots,v_n$ we will get
$$ e_1\equiv\frac{v_1}{\dnorm{v_1}}=\frac00 $$
That is, we get division by zero, which is not allowed and undefined. Hence Gram-Schdmit breaks.
If $v_1\neq0$, then by the Linear Dependence Lemma (2.21), there exists some $k$ such that $v_{k+1}\in\span{v_1,\dots,v_k}$. Here we choose the smallest such $k$. That is, the list $v_1,\dots,v_k$ is linearly independent.
Suppose we apply Gram-Schdmit to $v_1,\dots,v_k,v_{k+1}$. At the $k^{th}$ step, proposition 6.31 implies that $\span{e_1,\dots,e_k}=\span{v_1,\dots,v_k}$. Hence we get an orthonormal basis $e_1,\dots,e_k$ for $\span{v_1,\dots,v_k}$. And since $v_{k+1}\in\span{v_1,\dots,v_k}$, then 6.30 implies
$$ v_{k+1}=\sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j $$
Then at step $k+1$, we get
$$ e_{k+1}\equiv\frac{v_{k+1}-\sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j}{\dnorm{v_{k+1}-\sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j}}=\frac0{\dnorm{0}}=\frac00 $$
Hence Gram-Schmidt breaks down when applied to a linearly dependent list. It’s interesting to note that, at step $k+1$ in the Gram-Schmidt procedure, the term $\sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j$ is the orthogonal projection of $v_{k+1}$ onto $\span{v_1,\dots,v_k}$ (by 6.55(i)). That is
$$ \sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j=P_{\span{v_1,\dots,v_k}}v_{k+1} $$
Then proposition 6.47 gives the inclusion
$$ v_{k+1}-\sum_{j=1}^k\innprd{v_{k+1}}{e_j}e_j=v_{k+1}-P_{\span{v_1,\dots,v_k}}v_{k+1}\in\span{v_1,\dots,v_k}^\perp $$
This of course is one of the purposes of the Gram Schmidt procedure (the other being normalization). $\blacksquare$
(10) Suppose $V$ is a real inner product space and $v_1,\dots,v_m$ is a linearly independent list of vectors in $V$. Then there exist exactly $2^m$ orthonormal lists $e_1,\dots,e_m$ of vectors in $V$ such that
$$ \span{v_1,\dots,v_j}=\span{e_1,\dots,e_j} $$
for all $j\in\set{1,\dots,m}$.
Proof For intuition, pick the linearly independent list $(0,1),(1,0)$ in $\wR^2$. Notice that there are an infinite number of orthonormal lists $e_1,e_2$ in $\wR^2$ such that
$$ \spanb{(1,0),(0,1)}=\span{e_1,e_2} $$
But there are only $4$ such orthonormal lists where we also have $\spanb{(1,0)}=\span{e_1}$. Namely, they are
$$ (0,1),(1,0) \quad\quad\quad (0,1),(-1,0) \quad\quad\quad (0,-1),(-1,0) \quad\quad\quad (0,-1),(1,0) $$
We will prove this by induction. Notice that there are only two vectors in $\span{v_1}$ with norm $1$. Those two vectors are $\frac{v_1}{\dnorm{v_1}}$ and $-\frac{v_1}{\dnorm{v_1}}$ (by W.6.G.6). Hence there are $2=2^1$ choices for $e_1$. Both choices satisfy $\span{v_1}=\span{e_1}$ since $\dim{\span{v_1}}=1$ and $e_1\neq0$.
Our induction assumption is that, for any $j=2,\dots,m$, there are exactly $2^{j-1}$ orthonormal lists $e_1,\dots,e_{j-1}$ such that
$$ \span{v_1,\dots,v_k}=\span{e_1,\dots,e_k} $$
for $k\in\set{1,\dots,j-1}$. Then the Gram-Schmidt procedure produces $e_j\in V$ such that
$$ \span{v_1,\dots,v_{j-1},v_j}=\span{e_1,\dots,e_{j-1},e_j} \tag{6.B.10.1} $$
This equality holds from 6.31.
Suppose $e_j’\in V$ is another vector with these properties, meaning that $e_1,\dots,e_{j-1},e_j’$ is an orthonormal list and
$$ \span{v_1,\dots,v_{j-1},v_j}=\span{e_1,\dots,e_{j-1},e_j'} \tag{6.B.10.2} $$
Combining 6.B.10.1 and 6.B.10.2, we see that
$$ \span{e_1,\dots,e_{j-1},e_j'}=\span{e_1,\dots,e_{j-1},e_j} $$
In particular, $e_j’\in\span{e_1,\dots,e_{j-1},e_j}$. Then 6.30 gives the first equality
$$ e_j'=\sum_{k=1}^j\innprd{e_j'}{e_k}e_k=\innprd{e_j'}{e_j}e_j \tag{6.B.10.3} $$
and the second equality holds because $e_1,\dots,e_{j-1},e_j’$ is an orthonormal list. Taking the norms of both sides, we get
$$ 1=\dnorm{e_j'}=\dnorm{\innprd{e_j'}{e_j}e_j}=\normw{\innprd{e_j'}{e_j}}\dnorm{e_j}=\normw{\innprd{e_j'}{e_j}} $$
since $e_j$ and $e_j’$ are both unit-norm vectors. Hence $\innprd{e_j’}{e_j}=\pm1$. Plugging this back into 6.B.10.3, we get
$$ e_j'=\innprd{e_j'}{e_j}e_j=\pm e_j $$
Hence there are exactly $2$ choices for $e_j$. Hence there are exactly $2^{j-1}2=2^j$ orthonormals lists $e_1,\dots,e_j$ such that
$$ \span{v_1,\dots,v_k}=\span{e_1,\dots,e_k} $$
for $k\in\set{1,\dots,j}$. Since this is true for any $j=2,\dots,m$, then we can choose $j=m$. $\blacksquare$
(11) Suppose $\innprd{\cdot}{\cdot}_1$ and $\innprd{\cdot}{\cdot}_2$ are inner products on $V$ such that $\innprd{v}{w}_1=0$ if and only if $\innprd{v}{w}_2=0$. Then there is a positive number $c$ such that $\innprd{v}{w}_1=c\innprd{v}{w}_2$ for every $v,w\in V$.
Proof Let $v,w\in V$. The hypothesis states that $v$ and $w$ are orthogonal relative to $\innprd{\cdot}{\cdot}_1$ if and only if they’re orthogonal relative to $\innprd{\cdot}{\cdot}_2$.
First suppose that $v$ and $w$ are orthogonal relative to $\innprd{\cdot}{\cdot}_1$. Then $\innprd{v}{w}_1=0$ and $\innprd{v}{w}_2=0$. Then any positive number $c$ will satisfy $\innprd{v}{w}_1=c\innprd{v}{w}_2$.
Now suppose that $v$ and $w$ are not orthogonal relative to $\innprd{\cdot}{\cdot}_1$. Then $\innprd{v}{w}_1\neq0$ and $\innprd{v}{w}_2\neq0$. Hence $v\neq0$ (by 6.7(b)) and $w\neq0$ (by 6.7.(c)). Then the definiteness of an inner product implies that
$$ \innprd{v}{v}_1\neq0 \quad\quad\quad \innprd{v}{v}_2\neq0 \quad\quad\quad \innprd{w}{w}_1\neq0 \quad\quad\quad \innprd{w}{w}_2\neq0 $$
Hence
$$\align{ 0 &= \innprd{v}{w}_1-\innprd{v}{w}_1 \\ &= \innprd{v}{w}_1-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}\innprd{v}{v}_1 \\ &= \innprd{v}{w}_1+\innprdBg{v}{\overline{\Prn{-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}}}v}_1 \\ &= \innprdBg{v}{w+\overline{\Prn{-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}}}v}_1 \\ &= \innprdBg{v}{w+\overline{\Prn{-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}}}v}_2\tag{by supposition} \\ &= \innprd{v}{w}_2+\innprdBg{v}{\overline{\Prn{-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}}}v}_2 \\ &= \innprd{v}{w}_2-\frac{\innprd{v}{w}_1}{\innprd{v}{v}_1}\innprd{v}{v}_2 \\ &= \innprd{v}{w}_2-\frac{\innprd{v}{v}_2}{\innprd{v}{v}_1}\innprd{v}{w}_1 \\ }$$
Hence
$$ \frac{\innprd{v}{v}_2}{\innprd{v}{v}_1}\innprd{v}{w}_1=\innprd{v}{w}_2 $$
or
$$ \innprd{v}{w}_1=\frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}\innprd{v}{w}_2 \tag{6.B.11.1} $$
Similarly
$$\align{ 0 &= \innprd{v}{w}_1-\innprd{v}{w}_1 \\ &= \innprd{v}{w}_1-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}\innprd{w}{w}_1 \\ &= \innprd{v}{w}_1+\innprdBg{-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}w}{w}_1 \\ &= \innprdBg{v-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}w}{w}_1 \\ &= \innprdBg{v-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}w}{w}_2\tag{by supposition} \\ &= \innprd{v}{w}_2+\innprdBg{-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}w}{w}_2 \\ &= \innprd{v}{w}_2-\frac{\innprd{v}{w}_1}{\innprd{w}{w}_1}\innprd{w}{w}_2 \\ &= \innprd{v}{w}_2-\frac{\innprd{w}{w}_2}{\innprd{w}{w}_1}\innprd{v}{w}_1 \\ }$$
Hence
$$ \frac{\innprd{w}{w}_2}{\innprd{w}{w}_1}\innprd{v}{w}_1=\innprd{v}{w}_2 $$
or
$$ \innprd{v}{w}_1=\frac{\innprd{w}{w}_1}{\innprd{w}{w}_2}\innprd{v}{w}_2 $$
Combining this with 6.B.11.1, we get
$$ \frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}\innprd{v}{w}_2=\innprd{v}{w}_1=\frac{\innprd{w}{w}_1}{\innprd{w}{w}_2}\innprd{v}{w}_2 $$
By assumption, we have $\innprd{v}{w}_1\neq0$ and $\innprd{v}{w}_2\neq0$. Hence
$$ \frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}=\frac{\innprd{w}{w}_1}{\innprd{w}{w}_2} $$
Hence we can define
$$ c\equiv\frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}=\frac{\innprd{w}{w}_1}{\innprd{w}{w}_2} $$
Notice that if we performed the same steps as above with $v$ and another abritrary nonzero vector in $V$, say $a$, then we would get
$$ \frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}\innprd{v}{a}_2=\innprd{v}{a}_1=\frac{\innprd{a}{a}_1}{\innprd{a}{a}_2}\innprd{v}{a}_2 $$
and
$$ c=\frac{\innprd{v}{v}_1}{\innprd{v}{v}_2}=\frac{\innprd{a}{a}_1}{\innprd{a}{a}_2} $$
That is, $c$ does not depend on $v$, $w$, or any other nonzero vector. Also note that $c>0$ by the positivity and definiteness properties of an inner product. $\blacksquare$
(12) Suppose $V$ is finite-dimensional and $\innprd{\cdot}{\cdot}_1,\innprd{\cdot}{\cdot}_2$ are inner products on $V$ with corresponding norms $\dnorm{\cdot}_1$ and $\dnorm{\cdot}_2$. Then there exists a positive number $c$ such that
$$ \dnorm{v}_1\leq c\dnorm{v}_2 $$
for every $v\in V$.
Proof Let $e_1,\dots,e_n$ be an orthonormal basis of $V$ relative to $\innprd{\cdot}{\cdot}_1$. Let $f_1,\dots,f_n$ be an orthonormal basis of $V$ relative to $\innprd{\cdot}{\cdot}_2$. Is there some linear functional $\varphi\in\linmap{V}{\mathbb{F}}$ such that
$$ \sum_{k=1}^n\normw{\innprd{v}{e_k}_1}^2\leq\normw{\varphi(v)}^2 $$
If so, then we have
$$\align{ \dnorm{v}_1^2 &= \sum_{k=1}^n\normw{\innprd{v}{e_k}_1}^2\tag{by 6.30} \\ &\leq \normw{\varphi(v)}^2 \\ &= \normw{\innprdBg{v}{\sum_{k=1}^n\overline{\varphi(f_k)}f_k}_2}^2\tag{by Riesz Representation 6.42} \\ &\leq \dnorm{v}_2^2\dnorm{\sum_{k=1}^n\overline{\varphi(f_k)}f_k}_2^2\tag{by Cauchy-Schwarz 6.15} \\ }$$
(13) Suppose $v_1,\dots,v_m$ is a linearly independent list in $V$. Then there exists $w\in V$ such that $\innprd{w}{v_j}>0$ for all $j\in\set{1,\dots,m}$.
Proof Proposition 3.5 gives the existence of the linear functional $\varphi\in\linmap{\span{v_1,\dots,v_m}}{\wF}$ defined by $\varphi(v_j)\equiv1$ for $j=1,\dots,m$. Then the Riesz Representation Theorem (6.42) gives the existence of $w\in\span{v_1,\dots,v_m}\subset V$ such that $\varphi(v)=\innprd{v}{w}$ for every $v\in\span{v_1,\dots,v_m}$. In particular
$$ \innprd{w}{v_j}=\overline{\innprd{v_j}{w}}=\overline{\varphi(v_j)}=\overline{1}=1>0 $$
for all $j\in\set{1,\dots,m}$. $\blacksquare$
(14) Suppose $e_1,\dots,e_n$ is an orthonormal basis of $V$ and $v_1,\dots,v_n$ are vectors in $V$ such that
$$ \dnorm{e_j-v_j}<\frac1{\sqrt{n}} $$
for each $j$. Then $v_1,\dots,v_n$ is a basis of $V$.
Proof Since $e_1,\dots,e_n$ is an orthonormal basis of $V$, then $\dim{V}=n$. To show that $v_1,\dots,v_n$ is a basis of $V$, it suffices to show that $v_1,\dots,v_n$ is linearly independent (by 2.39). We will prove this by contradiction.
Suppose $v_1,\dots,v_n$ is linearly dependent. Then there exist $a_1,\dots,a_n\in\wF$ not all zero such that
$$ \sum_{j=1}^na_jv_i=0 $$
By 6.25, we have
$$ \dnorm{\sum_{j=1}^na_j(e_j-v_j)}^2=\dnorm{\sum_{j=1}^na_je_j-\sum_{j=1}^na_jv_j}^2=\dnorm{\sum_{j=1}^na_je_j}^2=\sum_{j=1}^n\normw{a_j}^2 \tag{6.B.14.1} $$
On the other hand, we have
$$\align{ \dnorm{\sum_{j=1}^na_j(e_j-v_j)}^2 &= \innprdBg{\sum_{j=1}^na_j(e_j-v_j)}{\sum_{k=1}^na_k(e_k-v_k)} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprdbg{a_j(e_j-v_j)}{a_k(e_k-v_k)}\tag{by additivity in each slot} \\ &= \sum_{j=1}^n\sum_{k=1}^n\normB{\innprdbg{a_j(e_j-v_j)}{a_k(e_k-v_k)}}\tag{by 6.3 positivity} \\ &= \sum_{j=1}^n\sum_{k=1}^n\dnormb{a_j(e_j-v_j)}\dnormb{a_k(e_k-v_k)}\tag{by 6.15 Cauchy-Schwarz} \\ &= \sum_{j=1}^n\sum_{k=1}^n\norm{a_j}\norm{a_k}\dnormb{(e_j-v_j)}\dnormb{(e_k-v_k)}\tag{by 6.10(b)} \\ &< \sum_{j=1}^n\sum_{k=1}^n\norm{a_j}\norm{a_k}\frac1{\sqrt{n}}\frac1{\sqrt{n}}\tag{6.B.14.2} \\ &= \sum_{j=1}^n\sum_{k=1}^n\norm{a_j}\norm{a_k}\frac1{n} \\ &= \frac1{n}\sum_{j=1}^n\sum_{k=1}^n\norm{a_j}\norm{a_k} \\ &= \frac1{n}\sum_{j=1}^n\norm{a_j}\sum_{k=1}^n\norm{a_k} \\ &= \frac1{n}\Prn{\sum_{k=1}^n\norm{a_k}}\Prn{\sum_{j=1}^n\norm{a_j}} \\ &= \frac1{n}\Prn{\sum_{j=1}^n\norm{a_j}}^2 \\ &\leq \sum_{j=1}^n\norm{a_j}^2\tag{by exercise 6.A.12} \\ }$$
Note that 6.B.14.2 holds for two reasons. We assumed that not all of the $a_j$’s are zero. If they were all zero, then the strict inequality would not hold. Instead it would be the equality $0=0$. The other reason this holds is because of the hypothesis that $\dnorm{e_j-v_j}<1/\sqrt{n}$.
Then 6.B.14.1 gives the next equality and the above gives the next inequality:
$$ \sum_{j=1}^n\normw{a_j}^2=\dnorm{\sum_{j=1}^na_j(e_j-v_j)}^2<\sum_{j=1}^n\norm{a_j}^2 $$
Hence we have a contradiction. $\blacksquare$
Exercises 6.C
(1) Suppose $v_1,\dots,v_m\in V$. Then
$$ \cbr{v_1,\dots,v_m}^\perp=\prn{\span{v_1,\dots,v_m}}^\perp $$
Proof Let $u\in\cbr{v_1,\dots,v_m}^\perp$. And let $v\in\span{v_1,\dots,v_m}$. Then
$$\begin{align*} \innprd{u}{v} = \innprdBg{u}{\sum_{j=1}^ma_jv_j} = \sum_{j=1}^m\innprd{u}{a_jv_j} = 0 \end{align*}$$
The last equality holds because $u$ is orthogonal to each of the $v_1,\dots,v_m$ and scaling preserves orthogonality. Hence $u\in\prn{\span{v_1,\dots,v_m}}^\perp$ and $\cbr{v_1,\dots,v_m}^\perp\subset\prn{\span{v_1,\dots,v_m}}^\perp$.
In the other direction, let $v\in\prn{\span{v_1,\dots,v_m}}^\perp$ and let $v_k\in\cbr{v_1,\dots,v_m}$. Then $v_k\in\span{v_1,\dots,v_m}$. Hence $v$ is orthogonal to $v_k$ and $\prn{\span{v_1,\dots,v_m}}^\perp\subset\cbr{v_1,\dots,v_m}^\perp$. $\blacksquare$
(2) Suppose $U$ is a finite-dimensional subspace of $V$. Then $U^\perp=\cb{0}$ if and only if $U=V$.
Exercise 14(a) shows that this result is not true without the hypothesis that $U$ is finite-dimensional.
Proof Suppose $U=V$ and let $u\in U^\perp\subset V$. Then $u$ is orthogonal to every vector in $V=U$. Hence $u$ is orthogonal to itself. Hence $u=0$ (by 6.12.b).
Suppose $U^\perp=\cb{0}$ and let $v\in V$. Since $V=U\oplus U^\perp$ (by 6.47), then $v=u+0=u$ for some $u\in U$. Hence $V\subset U$. $\blacksquare$
(3) Suppose $U$ is a subspace of $V$ with basis $u_1,\dots,u_m$ and
$$ u_1,\dots,u_m,w_1,\dots,w_n $$
is a basis of $V$. If the Gram-Schmidt procedure is applied to this basis of $V$, producing a list $e_1,\dots,e_m,f_1,\dots,f_n$, then $e_1,\dots,e_m$ is an orthonormal basis of $U$ and $f_1,\dots,f_n$ is an orthonormal basis of $U^\perp$
Proof We will show by induction that $e_k\in U$. Clearly $e_1=u_1/\dnorm{u_1}\in U$ since $u_1\in U$. Our induction assumption is that $e_1,\dots,e_{k-1}\in U$ for $1<k<m$. Hence
$$ e_k=\frac{u_k-\sum_{j=1}^{k-1}\innprd{u_k}{e_j}e_j}{\dnorm{u_k-\sum_{j=1}^{k-1}\innprd{u_k}{e_j}e_j}}\in\span{u_k,e_1,\dots,e_{k-1}}\subset U $$
Since $\dim{U}=m$ and $e_1,\dots,e_m\in U$ is an orthonormal list of the right length, then it’s an orthonormal basis (by 6.28) of $U$.
To show that $f_i\in U^\perp$, it’s suffices (by W.6.G.1) to show that $f_i$ is orthogonal to each vector in the orthonormal basis $e_1,\dots,e_m$ of $U$. But $e_1,\dots,e_m,f_1,\dots,f_n$ is an orthonormal list so this must be true.
Hence $f_1,\dots,f_n$ is an orthonormal list in $U^\perp$ and it suffices (by 6.28) to show that $\dim{U^\perp}=n$:
$$ \dim{U^\perp}=\dim{V}-\dim{U}=\len{e_1,\dots,e_m,f_1,\dots,f_n}-m=m+n-m=n $$
The first equality follows from 6.50. $\blacksquare$
(4) Suppose $U$ is the subspace of $\mathbb{R}^4$ defined by
$$ U\equiv\spanb{(1,2,3,-4),(-5,4,3,2)} $$
Find an orthonormal basis of $U$ and an orthonormal basis of $U^\perp$.
Solution Let’s first check if $v_1\equiv(1,2,3,-4)$ and $v_2\equiv(-5,4,3,2)$ are linearly independent.
$$ 0=a_1v_1+a_2v_2=(a_1,2a_1,3a_1,-4a_1)+(-5a_2,4a_2,3a_2,2a_2) $$
This becomes the system
$$\begin{align*} a_1-5 a_2 & = 0 \\ 2 a_1+4 a_2 & = 0 \\ 3 a_1+3 a_2 & = 0 \\ -4 a_1+2 a_2 & = 0 \end{align*}$$
Let’s compute:
$$ \bmtrx{1&-5&0\\2&4&0\\3&3&0\\-4&2&0} \rightarrow \bmtrx{1&-5&0\\0&10+4&0\\0&15+3&0\\0&2-20&0} \rightarrow \bmtrx{1&-5&0\\0&14&0\\0&18&0\\0&-18&0} \rightarrow \bmtrx{1&-5&0\\0&14&0\\0&18&0\\0&0&0} $$
$$ \rightarrow \bmtrx{1&-5&0\\0&14&0\\0&18-\frac{18}{14}14&0\\0&0&0} \rightarrow \bmtrx{1&-5&0\\0&14&0\\0&0&0\\0&0&0} \rightarrow \bmtrx{1&-5&0\\0&1&0\\0&0&0\\0&0&0} \rightarrow \bmtrx{1&0&0\\0&1&0\\0&0&0\\0&0&0} $$
So $v_1,v_2$ is linearly independent. By the preceding problem, it will be easiest to first extend this list to a basis of $\mathbb{R}^4$. It seems likely that $w_1\equiv(0,0,1,0)$ and $w_2\equiv(0,0,0,1)$ will be linearly independent with $v_1,v_2$:
$$\begin{align*} a_1-5 a_2 +0a_3+0a_4 & = 0 \\ 2 a_1+4 a_2 +0a_3+0a_4 & = 0 \\ 3 a_1+3 a_2 +1a_3+0a_4 & = 0 \\ -4 a_1+2 a_2 +0a_3+1a_4 & = 0 \end{align*}$$
Hence
$$ \bmtrx{1&-5&0&0&0\\2&4&0&0&0\\3&3&1&0&0\\-4&2&0&1&0} \rightarrow \bmtrx{1&-5&0&0&0\\0&10+4&0&0&0\\0&15+3&1&0&0\\0&2-20&0&1&0} \rightarrow \bmtrx{1&-5&0&0&0\\0&14&0&0&0\\0&18&1&0&0\\0&-18&0&1&0} $$
$$ \rightarrow \bmtrx{1&-5&0&0&0\\0&1&0&0&0\\0&18&1&0&0\\0&-18&0&1&0} \rightarrow \bmtrx{1&-5+5\cdot1&0&0&0\\0&1&0&0&0\\0&18-18\cdot1&1&0&0\\0&-18+18\cdot1&0&1&0} \rightarrow \bmtrx{1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0} $$
Then applying Gram-Schmidt, we get
$$ e_1=\frac{v_1}{\dnorm{v_1}}=\frac{(1,2,3,-4)}{\sqrt{1+4+9+16}}=\frac{(1,2,3,-4)}{\sqrt{30}} $$
$$ e_2=\frac{v_2-\innprd{v_2}{e_1}e_1}{\dnorm{v_2-\innprd{v_2}{e_1}e_1}} $$
$$ f_1=\frac{w_1-\innprd{w_1}{e_1}e_1-\innprd{w_1}{e_2}e_2}{\dnorm{w_1-\innprd{w_1}{e_1}e_1-\innprd{w_1}{e_2}e_2}} $$
$$ f_2=\frac{w_2-\innprd{w_2}{e_1}e_1-\innprd{w_2}{e_2}e_2-\innprd{w_2}{w_1}w_1}{\dnorm{w_2-\innprd{w_2}{e_1}e_1-\innprd{w_2}{e_2}e_2-\innprd{w_2}{w_1}w_1}} $$
By the preceding exercise, $e_1,e_2$ is an orthonormal basis of $U$ and $f_1,f_2$ is an orthonormal basis of $U^\perp$. $\blacksquare$
(5) Suppose $V$ is finite-dimensional and $U$ is a subspace of $V$. Then $P_{U^\perp}=I-P_U$.
Proof Let $v\in V$. Then $v=u+w$ for some $u\in U$ and some $w\in U^\perp$ (by 6.47). Note that $u\in U=(U^\perp)^\perp$ (by 6.51). Hence $P_{U^\perp}v=w$ and
$$ (I-P_U)v=Iv-P_Uv=v-u=u+w-u=w=P_{U^\perp}v $$
$\blacksquare$
(6) Suppose $U$ and $W$ are finite-dimensional subspaces of $V$. Then $P_UP_W=0$ if and only if $\innprd{u}{w}=0$ for all $u\in U$ and all $w\in W$.
Proof Suppose $\innprd{u}{w}=0$ for all $u\in U$ and all $w\in W$. Then every vector in $W$ is orthogonal to every vector in $U$. Hence $W\subset U^\perp$. Let $v\in V$. Since $\mathscr{R}(P_W)=W$ (by 6.55(d)), then $P_Wv\in W\subset U^\perp$. Then 6.55(c) gives $P_U(P_Wv)=0$. Alternatively, we can uniquely write $P_Wv=0+P_Wv$ where $0\in U$ and $P_Wv\in U^\perp$ (by 6.47). Then
$$ P_UP_Wv=P_U(0+P_Wv)=0 $$
Conversely, suppose $P_UP_W=0$. Let $w\in W$. Then $P_Uw=w$ (by 6.55(b) or W.6.G.3) and $0=P_U(P_Ww)=P_Uw$. Hence $w\in\mathscr{N}(P_U)=U^\perp$ (by 6.55(a)). Hence $w$ is orthogonal to every $u\in U$. Hence $\innprd{u}{w}=0$ for every $u\in U$. Since $w$ was chosen arbitrarily, then $\innprd{u}{w}=0$ for all $u\in U$ and all $w\in W$. $\blacksquare$.
(7) Suppose $V$ is finite-dimensional and $P\in\oper{V}$ is such that $P^2=P$ and every vector in $\nullsp{P}$ is orthogonal to every vector in $\rangsp{P}$. Then there exists a subspace $U$ of $V$ such that $P=P_U$.
Note Cross-reference with counterexample W.6.G.4.
Proof Theorem 3.22 gives $\dim{\nullsp{P}}=\dim{V}-\dim{\rangsp{P}}$. And 6.50 gives $\dim{\rangsp{P}^\perp}=\dim{V}-\dim{\rangsp{P}}$. Hence $\dim{\nullsp{P}}=\dim{\rangsp{P}^\perp}$. Since every vector in $\nullsp{P}$ is orthogonal to $\rangsp{P}$, then $\nullsp{P}\subset\rangsp{P}^\perp$. Hence $\nullsp{P}=\rangsp{P}^\perp$ (by W.2.12).
We will show that $P=P_{\rangsp{P}}$. Let $v\in V$. Then $v=u+w$ for some $u\in\rangsp{P}$ and some $w\in\rangsp{P}^\perp$ (by 6.47). Then $P_{\rangsp{P}}v=u$ and
$$ Pv=P(u+w)=Pu+Pw=Pu $$
since $w\in\rangsp{P}^\perp=\nullsp{P}$. But $u\in\rangsp{P}$, so $u=Pz$ for some $z\in V$. Hence
$$ Pv=Pu=P(Pz)=P^2z=Pz=u=P_{\rangsp{P}}v $$
$\blacksquare$
Alternate Proof Let $v\in V$. Then (similar to exercise 5.B.4)
$$ v=Pv+(v-Pv) \tag{6.C.7.1} $$
Clearly $Pv\in\rangsp{P}$. Also, $P(v-Pv)=Pv-P^2v=0$ hence $v-Pv\in\nullsp{P}\subset\rangsp{P}^\perp$. Then 6.C.7.1 writes $v$ as a sum of a vector in $\rangsp{P}$ and a vector in $\rangsp{P}^\perp$. In this unique (by 6.47) decomposition, the vector in $\rangsp{P}$ equals, by definition, $P_{\rangsp{P}}v$. $\blacksquare$
(8) Suppose $V$ is finite-dimensional and $P\in\oper{V}$ is such that $P^2=P$ and
$$ \dnorm{Pv}\leq\dnorm{v} $$
for every $v\in V$. Then there exists a subspace $U$ of $V$ such that $P=P_U$.
Note Cross-reference with counterexample W.6.G.4.
Proof Let $u\in\rangsp{P}$ and $w\in\nullsp{P}$. By the previous exercise, it suffices to show that $\innprd{u}{w}=0$. Since $u\in\rangsp{P}$, then there exists $z\in V$ such that $u=Pz$. Applying $P$ to both sides of this equation, we get
$$ Pu=P(Pz)=P^2z=Pz=u $$
And because $w\in\nullsp{P}$, we get
$$ P(u+aw)=Pu+aPw=Pu=u $$
for every $a\in\wF$. Hence
$$ \dnorm{u}^2=\dnorm{P(u+aw)}^2\leq\dnorm{u+aw}^2 $$
for every $a\in\wF$. The inequality follows from the hypothesis that $\dnorm{Pv}\leq\dnorm{v}$ for every $v\in V$. And this inequality implies that $\innprd{u}{v}=0$ (by exercise 6.A.6). $\blacksquare$
(9) Suppose $T\in\oper{V}$ and $U$ is a finite-dimensional subspace of $V$. Then $U$ is invariant under $T$ if and only if $P_UTP_U=TP_U$.
Proof Suppose $P_UTP_U=TP_U$ and let $u\in U$. Then
$$ Tu=T(P_Uu)=(TP_U)u=(P_UTP_U)u=(P_UT)(P_Uu)=(P_UT)u=P_U(Tu) $$
Since $P_U(Tu)=Tu$, then the definition of orthogonal projection (6.53) implies that the orthogonal decomposition of $Tu$ is $Tu=Tu+0$ where $Tu\in U$ and $0\in U^\perp$.
Conversely, suppose $U$ is invariant under $T$ and let $v\in V$. Then $v=u+w$ for some $u\in U$ and some $w\in U^\perp$ (by 6.47). Hence
$$\align{ (P_UTP_U)v &= (P_UTP_U)(u+w) \\ &= (P_UTP_U)u+(P_UTP_U)w \\ &= (P_UT)(P_Uu)+(P_UT)(P_Uw) \\ &= (P_UT)u+(P_UT)(0) \\ &= P_U(Tu)+P_U(T(0)) \\ &= Tu+P_U(0) \\ &= Tu }$$
Similarly
$$\align{ (TP_U)v &= (TP_U)(u+w) \\ &= (TP_U)u+(TP_U)w \\ &= T(P_Uu)+T(P_Uw) \\ &= Tu+T(0) \\ &= Tu\quad\blacksquare }$$
(10) Suppose $V$ is finite-dimensional, $T\in\oper{V}$, and $U$ is a subspace of $V$. Then $U$ and $U^\perp$ are both invariant under $T$ if and only if $P_UT=TP_U$.
Proof Suppose $P_UT=TP_U$. Recall $P_U^2=P_U$ (by 6.55(g)). Then
$$ P_UTP_U=(P_UT)P_U=(TP_U)P_U=T(P_UP_U)=TP_U^2=TP_U $$
Then the previous exercise implies that $U$ is invariant under $T$. Now recall that exercise 6.C.5 gives $P_{U^\perp}=I-P_U$. Hence
$$\align{ P_{U^\perp}TP_{U^\perp} &= \prn{(I-P_U)T}P_{U^\perp} \\ &= (T-P_UT)P_{U^\perp}\tag{by W.3.20.1} \\ &= (T-TP_U)P_{U^\perp} \\ &= T(I-P_U)P_{U^\perp}\tag{by W.3.20.2} \\ &= TP_{U^\perp}P_{U^\perp} \\ &= TP_{U^\perp}^2 \\ &= TP_{U^\perp}\tag{by 6.55.g} }$$
Then the previous exercise implies that $U^\perp$ is invariant under $T$.
Conversely, suppose $U$ and $U^\perp$ are both invariant under $T$. Then the previous exercise implies that
$$ P_UTP_U=TP_U \tag{6.C.10.1} $$
and
$$ P_{U^\perp}TP_{U^\perp}=TP_{U^\perp} \tag{6.C.10.2} $$
Also note that
$$\align{ T-TP_U &= T(I-P_U)\tag{by W.3.20.2} \\ &= TP_{U^\perp}\tag{by exer 6.C.5} \\ &= P_{U^\perp}TP_{U^\perp}\tag{by 6.C.10.2} \\ &= (I-P_U)T(I-P_U) \\ &= (T-P_UT)(I-P_U)\tag{by W.3.20.1} \\ &= T-TP_U-P_UT+P_UTP_U\tag{by W.3.20.3} }$$
Subtracting $T-TP_U$ from both sides, we get $0=-P_UT+P_UTP_U$. Equivalently $P_UT=P_UTP_U$. Hence
$$ P_UT=P_UTP_U=TP_U\tag{by 6.C.10.1} $$
$\blacksquare$
(11) In $\wR^4$, define
$$ U\equiv\spanb{(1,1,0,0),(1,1,1,2)} $$
Find $u\in U$ such that $\dnorm{u-(1,2,3,4)}$ is as small as possible.
Proof Proposition 6.56 implies that for any $v\in U$, we have
$$ \dnorm{(1,2,3,4)-P_U(1,2,3,4)}\leq\dnorm{(1,2,3,4)-v} $$
So let’s compute $P_U(1,2,3,4)$. Proposition 6.55(a) gives us a convenient formula to do that:
$$ P_U(1,2,3,4)=\innprdbg{(1,2,3,4)}{e_1}e_1+\innprdbg{(1,2,3,4)}{e_2}e_2 \tag{6.C.11.1} $$
where $e_1,e_2$ is any orthonormal basis of $U$ (assuming that $\dim{U}=2$, which we will see is true). As we saw in exercise 6.B.9, if $(1,1,0,0),(1,1,1,2)$ is not linearly independent, then Gram-Schmidt won’t work. So let’s first check that and also conclude that $\dim{U}=2$.
$$\align{ (0,0,0,0) &= a(1,1,0,0)+b(1,1,1,2) \\ &= (a,a,0,0)+(b,b,b,2b) \\ &= (a+b,a+b,b,2b) }$$
Hence $b=0$ and $a+b=0$. Hence $a=0$ and $(1,1,0,0),(1,1,1,2)$ is linearly independent. Now we apply Gram-Schmidt:
$$ e_1\equiv\frac{(1,1,0,0)}{\dnorm{(1,1,0,0)}}=\frac{(1,1,0,0)}{\sqrt{2}}=\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} $$
Note that
$$\align{ (1,1,1,2)-\innprdbg{(1,1,1,2)}{e_1}e_1 &= (1,1,1,2)-\innprdBg{(1,1,1,2)}{\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0}}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= (1,1,1,2)-\Cbr{\frac1{\sqrt2}+\frac1{\sqrt2}}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= (1,1,1,2)-\frac2{\sqrt2}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= (1,1,1,2)-\Prn{\frac2{\sqrt2}\frac1{\sqrt2},\frac2{\sqrt2}\frac1{\sqrt2},0,0} \\\\ &= (1,1,1,2)-(1,1,0,0) \\ &= (0,0,1,2) }$$
Hence
$$\align{ e_2 &\equiv \frac{(1,1,1,2)-\innprdbg{(1,1,1,2)}{e_1}e_1}{\dnorm{(1,1,1,2)-\innprdbg{(1,1,1,2)}{e_1}e_1}} \\\\ &= \frac{(0,0,1,2)}{\dnorm{(0,0,1,2)}} \\\\ &= \frac{(0,0,1,2)}{\sqrt{1+4}} \\\\ &= \Prn{0,0,\frac1{\sqrt5},\frac2{\sqrt5}} }$$
Note that
$$\align{ \innprdbg{(1,2,3,4)}{e_1}e_1 &= \innprdBg{(1,2,3,4)}{\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0}}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= \Cbr{\frac1{\sqrt2}+\frac2{\sqrt2}}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= \frac3{\sqrt2}\Prn{\frac1{\sqrt2},\frac1{\sqrt2},0,0} \\\\ &= \Prn{\frac3{\sqrt2}\frac1{\sqrt2},\frac3{\sqrt2}\frac1{\sqrt2},0,0} \\\\ &= \Prn{\frac32,\frac32,0,0} }$$
Hence
$$\align{ \innprdbg{(1,2,3,4)}{e_2}e_2 &= \innprdBg{(1,2,3,4)}{\Prn{0,0,\frac1{\sqrt5},\frac2{\sqrt5}}}\Prn{0,0,\frac1{\sqrt5},\frac2{\sqrt5}} \\\\ &= \Cbr{\frac3{\sqrt5}+\frac8{\sqrt5}}\Prn{0,0,\frac1{\sqrt5},\frac2{\sqrt5}} \\\\ &= \frac{11}{\sqrt5}\Prn{0,0,\frac1{\sqrt5},\frac2{\sqrt5}} \\\\ &= \Prn{0,0,\frac{11}{\sqrt5}\frac1{\sqrt5},\frac{11}{\sqrt5}\frac2{\sqrt5}} \\\\ &= \Prn{0,0,\frac{11}5,\frac{22}5} }$$
Then our orthogonal projection vector $P_U(1,2,3,4)$ from 6.C.11.1 is
$$\align{ P_U(1,2,3,4) &= \innprdbg{(1,2,3,4)}{e_1}e_1+\innprdbg{(1,2,3,4)}{e_2}e_2 \\\\ &= \Prn{\frac32,\frac32,0,0}+\Prn{0,0,\frac{11}5,\frac{22}5} \\\\ &= \Prn{\frac32,\frac32,\frac{11}5,\frac{22}5}\quad\blacksquare }$$
(12) Find $p\in\polyrn{3}$ such that $p(0)=0,p’(0)=0$, and
$$ \int_0^1\norm{2+3x-p(x)}^2dx $$
is as small as possible.
Proof Let $\mathscr{C}_{\wR}[0,1]$ denote the real inner product space of continuous real-valued functions on $[0,1]$ with inner product
$$ \innprd{f}{g}\equiv\int_0^1f(t)g(t)dt $$
Let $U$ denote the subspace of $\mathscr{C}_{\wR}[0,1]$ consisting of polynomials $u$ with degree at most $3$ and such that $u(0)=0,u’(0)=0$. Then $U$ is equivalent to the set of polynomials with degree at most $3$ and no terms with degrees $0$ or $1$. That is, every $u\in U$ is of the form $u=ax^2+bx^3$. It’s simple to verify that $U$ is closed under addition and scalar multiplication. And it seems clear that $x^2,x^3$ is a basis of $U$.
Define $v\in\mathscr{C}_{\wR}[0,1]$ by $v\equiv2x^0+3x^1$. That is, for $t\in[0,1]$, we have
$$ v(t)\equiv2x^0(t)+3x^1(t)=2+3t $$
Proposition 6.56 implies that for any $u\in U$, we have
$$ \dnorm{v-P_Uv}\leq\dnorm{v-u} $$
So let’s compute $P_Uv$. Proposition 6.55(a) gives us a convenient formula to do that:
$$ P_Uv=\innprd{v}{e_2}e_2+\innprd{v}{e_3}e_3 \tag{6.C.12.1} $$
where $e_2,e_3$ is any orthonormal basis of $U$. Let’s compute such a basis with Gram-Schmidt.
$$\align{ \dnorm{x^2} &= \sqrt{\innprd{x^2}{x^2}} \\ &= \sqrt{\int_0^1x^2(t)x^2(t)dt} \\ &= \sqrt{\int_0^1t^2t^2dt} \\ &= \sqrt{\int_0^1t^4dt} \\ &= \sqrt{\frac15\Prn{t^5\eval{0}{1}}} \\ &= \sqrt{\frac15(1^5-0^5)} \\ &= \frac1{\sqrt5} }$$
Hence
$$ e_2\equiv\frac{x^2}{\dnorm{x^2}}=\frac{x^2}{\frac1{\sqrt5}}=\sqrt5x^2 $$
and
$$\align{ \innprd{x^3}{e_2}e_2 &= \int_0^1x^3(t)e_2(t)dt\cdot e_2 \\ &= \sqrt5\int_0^1x^3(t)x^2(t)dt\cdot e_2 \\ &= \sqrt5\int_0^1x^5(t)dt\cdot e_2 \\ &= \sqrt5\int_0^1t^5dt\cdot e_2 \\ &= \sqrt5\cdot\frac16\Prn{t^6\eval01}\cdot e_2 \\ &= \sqrt5\cdot\frac16\cdot e_2 \\ &= \sqrt5\cdot\frac16\cdot\sqrt5x^2 \\ &= \frac56x^2 }$$
and
$$\align{ \dnorm{x^3-\innprd{x^3}{e_2}e_2} &= \dnorm{x^3-\frac56x^2} \\ &= \sqrt{\innprdBg{x^3-\frac56x^2}{x^3-\frac56x^2}} \\ &= \sqrt{\innprd{x^3}{x^3}+\innprdBg{x^3}{-\frac56x^2}+\innprdBg{-\frac56x^2}{x^3}+\innprdBg{-\frac56x^2}{-\frac56x^2}} \\ &= \sqrt{\innprd{x^3}{x^3}-\frac56\innprd{x^3}{x^2}-\frac56\innprd{x^2}{x^3}+\frac56\frac56\innprd{x^2}{x^2}} \\ &= \sqrt{\innprd{x^3}{x^3}-\frac{10}6\innprd{x^2}{x^3}+\frac{25}{36}\innprd{x^2}{x^2}} \\ &= \sqrt{\int_0^1x^6(t)dt-\frac{10}6\int_0^1x^5(t)dt+\frac{25}{36}\int_0^1x^4(t)dt} \\ &= \sqrt{\frac17-\frac{10}6\frac16+\frac{25}{36}\frac15} \\ &= \sqrt{\frac17-\frac{10}{36}+\frac5{36}} \\ &= \sqrt{\frac17-\frac5{36}} \\ &= \sqrt{\frac17\frac{36}{36}-\frac5{36}\frac77} \\ &= \sqrt{\frac{36}{7\cdot 36}-\frac{35}{7\cdot 36}} \\ &= \sqrt{\frac{36-35}{7\cdot 36}} \\ &= \sqrt{\frac{1}{7\cdot 36}} \\ &= \sqrt{\frac{1}{7}}\sqrt{\frac{1}{36}} \\ &= \frac1{\sqrt7}\frac16 \\ &= \frac1{6\sqrt7} }$$
Hence
$$\align{ e_3 &\equiv \frac{x^3-\innprd{x^3}{e_2}e_2}{\dnorm{x^3-\innprd{x^3}{e_2}e_2}} \\ &= \frac{x^3-\frac56x^2}{\frac1{6\sqrt7}} \\ &= 6\sqrt7\Prn{x^3-\frac56x^2} \\ &= \sqrt7\prn{6x^3-5x^2} \\ }$$
Note that
$$\align{ \innprd{v}{e_2} &= \int_0^1(2+3x)(t)(\sqrt5x^2)(t)dt \\ &= \sqrt5\int_0^1(2x^2+3x^3)(t)dt \\ &= \sqrt5\int_0^1(2t^2+3t^3)dt \\ &= \sqrt5\Cbr{\int_0^12t^2dt+\int_0^13t^3dt} \\ &= \sqrt5\Cbr{2\int_0^1t^2dt+3\int_0^1t^3dt} \\ &= \sqrt5\Cbr{2\cdot\frac13+3\cdot\frac14} \\ &= \sqrt5\Cbr{\frac23+\frac34} \\ &= \sqrt5\Cbr{\frac23\frac44+\frac34\frac33} \\ &= \sqrt5\Cbr{\frac{8}{12}+\frac{9}{12}} \\ &= \sqrt5\cdot\frac{17}{12} }$$
and
$$\align{ \innprd{v}{e_3} &= \int_0^1(2+3x)(t)\prn{\sqrt7(6x^3-5x^2)}(t)dt \\ &= \sqrt7\int_0^1(2+3x)(t)(6x^3-5x^2)(t)dt \\ &= \sqrt7\int_0^1\prn{(2+3x)(6x^3-5x^2)}(t)dt \\ &= \sqrt7\int_0^1(12x^3-10x^2+18x^4-15x^3)(t)dt \\ &= \sqrt7\int_0^1(-3x^3-10x^2+18x^4)(t)dt \\ &= \sqrt7\int_0^1(-3t^3-10t^2+18t^4)dt \\ &= \sqrt7\Cbr{\int_0^1(-3t^3)dt+\int_0^1(-10t^2)dt+\int_0^1(18t^4)dt} \\ &= \sqrt7\Cbr{-3\int_0^1t^3dt-10\int_0^1t^2dt+18\int_0^1t^4dt} \\ &= \sqrt7\Cbr{-3\cdot\frac14-10\cdot\frac13+18\cdot\frac15} \\ &= \sqrt7\Cbr{18\cdot\frac15-3\cdot\frac14-10\cdot\frac13} \\ &= \sqrt7\Cbr{\frac{18}5-\frac34-\frac{10}3} \\ &= \sqrt7\Cbr{\frac{18}5\frac{12}{12}-\frac34\frac{15}{15}-\frac{10}3\frac{20}{20}} \\ &= \sqrt7\Cbr{\frac{18\cdot12-45-200}{60}} \\ &= \sqrt7\Cbr{\frac{216-45-200}{60}} \\ &= \sqrt7\Cbr{\frac{16-45}{60}} \\ &= \sqrt7\Cbr{\frac{-29}{60}} \\ &= -\frac{29\sqrt7}{60} \\ }$$
Then our orthogonal projection vector $P_Uv$ in 6.C.12.1 becomes
$$\align{ P_Uv &= \innprd{v}{e_2}e_2+\innprd{v}{e_3}e_3 \\ &= \frac{17}{12}\sqrt5\sqrt5x^2-\frac{29\sqrt7}{60}\sqrt7(6x^3-5x^2) \\ &= \frac{17}{12}\cdot5\cdot x^2-\frac{29\cdot7}{60}(6x^3-5x^2) \\ &= \frac{17\cdot5}{12}x^2-\frac{29\cdot7\cdot6}{60}x^3+\frac{29\cdot7\cdot5}{60}x^2 \\ &= \frac{85}{12}x^2-\frac{29\cdot7}{10}x^3+\frac{29\cdot7}{12}x^2 \\ &= \frac{85}{12}x^2+\frac{29\cdot7}{12}x^2-\frac{29\cdot7}{10}x^3 \\ &= \frac{85}{12}x^2+\frac{203}{12}x^2-\frac{203}{10}x^3 \\ &= \frac{85+203}{12}x^2-\frac{203}{10}x^3 \\ &= \frac{288}{12}x^2-\frac{203}{10}x^3 \\ &= 24x^2-\frac{203}{10}x^3\quad\blacksquare }$$