One of my favorite books is Sheldon Axler’s Linear Algebra Done Right. I can’t say enough good things about this book. The clarity with which Professor Axler describes complex material is remarkable. Careful reading of the text and completion of most of the exercises vastly elevated my understanding of linear algebra. I strongly recommend this book to anyone with a suitable background.
Having said that, the author gives limited treatment to Singular Value Decomposition and Polar Decomposition. I presume the author’s intention was to keep a tight focus. But considering the breadth and strength of its applications, I really wanted to learn what SVD means, theoretically and geometrically.
This post is my attempt to describe the theory underlying Polar Decomposition and SVD. After a brief geometric description, I present the key propositions. We will work with abitrary inner product spaces $($not necessarily $\wR^n$ or $\wC^n)$ and the linear maps between them. When we work with matrices, it will always be with respect to a linear map and a basis or pair of bases. Later, I will present a couple of examples in $\wR^n$ to illustrate the computations and the geometry.
References & Notation
Throughout this post, I frequently reference various propositions and definitions from Axler’s book. I do this simply by number. For instance, the number 6.30 references proposition 6.30 on p.182 labeled “Writing a vector as linear combination of orthonormal basis”.
The key propositions presented here also reference a number of supporting propositions, all of which can be found in the Appendix, along with their proofs. These references are indicated by App.25, for example.
I generally use the notation from Professor Axler’s book. $\wF$ denotes either $\wR$ or $\wC$. $U$, $V$, and $W$ are inner product spaces. $U$ and $V$ are finite-dimensional and $W$ may be either finite or infinite-dimensional unless specified to one of them.
$\linmap{U}{V}$ is the vector space of linear maps from $U$ to $V$. If $u_1,\dots,u_n$ is a basis of $U$ and $v_1,\dots,v_n$ is a basis of $V$, then $\mtrxofb{T,(u_1,\dots,u_n),(v_1,\dots,v_n)}$ denotes the matrix of the linear map $T\in\linmap{U}{V}$ with respect to these bases. For brevity, I often denote a basis by $u\equiv u_1,\dots,u_n$. Hence $\mtrxof{T,u,v}=\mtrxofb{T,(u_1,\dots,u_n),(v_1,\dots,v_n)}$. The vector space of all $m\times n$ matrices with entries in $\wF$ is denoted by $\wF^{m\times n}$.
The range space of a linear map $T$ is denoted by $\rangsp{T}$. The null space of $T$ is denoted by $\nullsp{T}$. And, for $\lambda\in\wF$, the eigenspace of $T$ corresponding to $\lambda$ is denoted by $\eignsp{\lambda}{T}$.
The symbol $\adjt{}$ denotes either the conjugate transpose of a matrix or the adjoint of a linear map. Chapter 7 of Axler’s book describes the adjoint and its various properties. I also provide a brief description in the section titled Adjoint $\adjtT$. The transpose of a matrix will be denoted by a superscript lowercase $t$.
If $T$ is a positive operator, the symbol $\sqrt{T}$ denotes the unique positive square root of $T$ as defined by 7.33 and 7.44. Axler proves existence and uniqueness in 7.36.
Geometry of Polar Decomposition & SVD
Typically, Polar Decomposition is stated in terms of matrices: Any matrix $A\in\wF^{m\times n}$ with $m\geq n$ can be factored as $A=UP$ where $U\in\wF^{m\times n}$ has orthonormal columns and $P\in\wF^{n\times n}$ is positive semi-definite. When $\wF=\wR$ and $m=n$, Polar Decomposition expresses any matrix $A\in\wR^{n\times n}$ as a dilation $(P)$ followed by a rotation or reflection $(U)$.
Professor Axler describes this geometrical intepretation with an analogy between $\wC$ and $\oper{V}$. You can find this at the beginning of Section 7.D, p.233 or you can watch the video. This analogy makes clear the geometry of Polar Decomposition. It’s nothing more than the representation of an arbitrary linear map as a dilation and a rotation. But when we’re working with operators or linear maps, we speak in terms of positive operators and isometries.
Similarly, SVD is typically stated in terms of matrices: Any matrix $A\in\wF^{m\times n}$ with $m\geq n$ can be factored as $A=UD\adjt{V}$ where $U\in\wF^{m\times n}$ and $V\in\wF^{n\times n}$ have orthonormal columns and $D\in\wF^{n\times n}$ is diagonal. The geometric interpretation is similar to that of Polar Decomposition. $U$ and $V$ are rotations and $D$ is a dilation.
Let’s take an example. Define $A\in\wF^{2\times2}$ by
$$ A\equiv\pmtrx{1&\frac12\\\frac12&2} $$
Taking the SVD of $A$, we get
A = np.array( [1,1/2,1/2,2] ).reshape(2,2)
U,D,V=np.linalg.svd(A)
U
array([[ 0.38268343, 0.92387953],
[ 0.92387953, -0.38268343]])
D = np.diag(D)
D
array([[ 2.20710678, 0. ],
[ 0. , 0.79289322]])
V.T
array([[ 0.38268343, 0.92387953],
[ 0.92387953, -0.38268343]])
We see that $V^t$ and $U$ are rotation matrices since
c=np.arccos(V[0,0])
np.round(np.sin(c), 8)
0.92387953
To see how each of these matrices effects a vector, let’s look at some vectors in $\wR^2$ with the tail on the unit circle and the head pointing in the same direction as the tail but twice the length:
When we multiply $V^T$ by these vectors, we get
We see that the original vectors have been rotated but have not yet been stretched or compressed. To do that, we multiply by $D$:
We see that the horizontal vectors have been stretched by a factor of about $2.2$. To see this more clearly, you can zoom in on a particular section by selecting that section. Note that $2.2$ is the largest eigenvalue from the matrix $D$. And we see that the vertical vectors have been compressed by a factor of about $0.8$, which is the smallest eigenvalue. To get the full effect of $A$, we multiply by $U$:
Polar Decomposition & SVD
Proposition PLRDC.1 Let $T\in\linmap{V}{W}$ and let $f_1,\dots,f_n$ denote an orthonormal basis of $V$ consisting of eigenvectors of $\tat$ corresponding to eigenvalues $\lambda_1,\dots,\lambda_n$ (existence given by the Spectral Theorem). App.2 and 7.35(b) imply that all of the $\lambda$’s are nonnegative. Without loss of generality, assume that $\lambda_1,\dots,\lambda_r$ are positive and that $\lambda_{r+1},\dots,\lambda_n$ are zero (re-index if necessary). Then
(A) $f_1,\dots,f_r$ is an orthonormal basis of $\rangspb{\sqrttat}$
(B) $f_{r+1},\dots,f_n$ is an orthonormal basis of $\rangspb{\sqrttat}^\perp=\nullspb{\sqrttat}=\nullsp{T}$
(C) $\rangsp{T}=\span{Tf_1,\dots,Tf_r}$
(D) $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ is an orthonormal basis of $\rangsp{T}$
(E) $\dim{\rangspb{\sqrttat}}=\dim{\rangsp{T}}=r$
(F) If $\dim{W}\geq\dim{V}$, then $\dim{\rangsp{T}^\perp}\geq\dim{V}-r$
(G) $\adjtT h=0$ for all $h\in\rangsp{T}^\perp$
Proof of (A) & (B) App.8 gives $\nullspb{\sqrttat}=\rangspb{\sqrttat}^\perp=\nullsp{T}$. So to prove (B), it suffices to show that $f_{r+1},\dots,f_n$ is an orthonormal basis of $\nullspb{\sqrttat}$.
Note that
$$ \tat f_j\equiv\lambda_j f_j\qd\text{for }j=1,\dots,n $$
App.2 gives
$$ \sqrttat f_j\equiv\sqrt{\lambda_j}f_j\qd\text{for }j=1,\dots,n $$
In particular, for $j=r+1,\dots,n$, we have $\sqrttat f_j=0\cdot f_j=0$. Hence
$$ f_{r+1},\dots,f_n\in\nullspb{\sqrttat} $$
Also note that App.9 gives
$$ \dim{\nullspb{\sqrttat}}=\dim{\eignspb{0}{\sqrttat}}=\text{number of }\lambda_j\text{'s equal to }0=n-r $$
Hence $f_{r+1},\dots,f_n$ is an orthonormal basis of $\nullspb{\sqrttat}$ (by 6.28). Hence
$$ \nullspb{\sqrttat}=\span{f_{r+1},\dots,f_n} $$
Also, since $f_1,\dots,f_n$ is orthonormal, then $f_j\in\setb{f_{r+1},\dots,f_n}^\perp$ for $j=1,\dots,r$. Then App.24 gives the first equality:
$$ f_j\in\setb{f_{r+1},\dots,f_n}^\perp=\prn{\span{f_{r+1},\dots,f_n}}^\perp=\nullspb{\sqrttat}^\perp\qd\text{for }j=1,\dots,r $$
Also note that $\sqrttat$ is positive, by definition 7.44 (also can be seen from App.1). Hence $\sqrttat$ is self-adjoint. This gives the second equality and the first equality follows from 7.7(b):
$$ f_1,\dots,f_r\in\nullspb{\sqrttat}^\perp = \rangspb{\adjt{\prn{\sqrttat}}} = \rangspb{\sqrttat} $$
Lastly, the Fundamental Theorem of Linear Maps (3.22) gives
$$ \dim{\rangspb{\sqrttat}}=\dim{V}-\dim{\nullspb{\sqrttat}}=n-(n-r)=r $$
Hence $f_1,\dots,f_r$ is an orthonormal basis of $\rangspb{\sqrttat}$ (by 6.28). $\wes$
Proof of (C) & (D) & (E) Let $w\in\rangsp{T}$. Then $w=Tv$ for some $v\in V$ and $v=\sum_{j=1}^n\innprd{v}{f_j}f_j$ (by 6.30). Hence
$$ w=Tv=T\Prngg{\sum_{j=1}^n\innprd{v}{f_j}f_j}=\sum_{j=1}^n\innprd{v}{f_j}Tf_j=\sum_{j=1}^r\innprd{v}{f_j}Tf_j\in\span{Tf_1,\dots,Tf_r} $$
The last equality holds because part (B) gives $Tf_j=0$ for $j=r+1,\dots,n$. Hence $\rangsp{T}\subset\span{Tf_1,\dots,Tf_r}$.
Conversely, we have $Tf_1,\dots,Tf_r\in\rangsp{T}$. Since $\rangsp{T}$ is closed under addition and scalar multiplication, then $\rangsp{T}$ contains any linear combination of $Tf_1,\dots,Tf_r$. Hence $\span{Tf_1,\dots,Tf_r}\subset\rangsp{T}$.
For $j,k=1,\dots,r$, we have
$$\align{ \innprdBgg{\frac1{\sqrt{\lambda_j}}Tf_j}{\frac1{\sqrt{\lambda_k}}Tf_k}_W &= \frac1{\sqrt{\lambda_j}}\frac1{\sqrt{\lambda_k}}\innprdbg{Tf_j}{Tf_k}_W \\ &= \frac1{\sqrt{\lambda_j}}\frac1{\sqrt{\lambda_k}}\innprdbg{f_j}{\tat f_k}_V \\ &= \frac1{\sqrt{\lambda_j}}\frac1{\sqrt{\lambda_k}}\innprdbg{f_j}{\lambda_kf_k}_V \\ &= \frac1{\sqrt{\lambda_j}}\frac{\lambda_k}{\sqrt{\lambda_k}}\innprd{f_j}{f_k}_V \\ &= \frac{\sqrt{\lambda_k}}{\sqrt{\lambda_j}}\innprd{f_j}{f_k}_V \\ &= \cases{1&j=k\\0&j\neq k} }$$
Hence $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ is an orthonormal list in $\rangsp{T}$. By 6.26, $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ is linearly independent. By part (C), $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ spans $\rangsp{T}$. Hence $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ is an orthonormal basis of $\rangsp{T}$.
Hence $\dim{\rangspb{\sqrttat}}=\dim{\rangsp{T}}=r$. $\wes$
Proof of (F) & (G) 6.50 gives
$$ \dim{\rangsp{T}^\perp}=\dim{W}-\dim{\rangsp{T}}\geq \dim{V}-r $$
and Adj.3 gives
$$ \adjtT h=\sum_{j=1}^n\innprd{h}{Tf_j}f_j=0 $$
since $h\in\rangsp{T}^\perp$ and $Tf_j\in\rangsp{T}$ for $j=1,\dots,n$. $\wes$
Example PLRDC.1.a Define $T\in\linmap{\wR}{\wR^2}$ by
$$ Te_1\equiv g_1+g_2 \dq\text{or}\dq \mtrxof{T,e,g}\equiv\pmtrx{1\\1} $$
where $e\equiv e_1=(1)$ is the standard basis of $\wR$ and $g\equiv g_1,g_2$ is the standard basis of $\wR^2$. Then
$$ Tx=T(xe_1)=xTe_1=x(g_1+g_2)=xg_1+xg_2=(x,x) \dq\text{or}\dq \mtrxof{T,e,g}\pmtrx{x}=\pmtrx{1\\1}\pmtrx{x}=\pmtrx{x\\x} $$
Hence $\rangsp{T}=\setb{(x,x)\in\wR^2:x\in\wR}$. Hence $\rangsp{T}^\perp=\setb{(x,-x)\in\wR^2:x\in\wR}$. Also
$$ \innprdbg{(x)}{\adjtT(y_1,y_2)}_{\wR} = \innprdbg{T(x)}{(y_1,y_2)}_{\wR^2} = \innprdbg{(x,x)}{(y_1,y_2)}_{\wR^2} = xy_1+xy_2 = \innprdbg{(x)}{(y_1+y_2)}_{\wR} $$
Hence $\adjtT(y_1,y_2)=y_1+y_2$. Hence $\tat x=\adjtT(x,x)=2x$. Or
$$ \mtrxof{\tat,e,e}=\mtrxof{\adjtT,g,e}\mtrxof{T,e,g}=\adjt{\mtrxof{T,e,g}}\mtrxof{T,e,g}=\pmtrx{1&1}\pmtrx{1\\1}=\pmtrx{2} $$
So $e_1$ is an orthonormal basis of $\wR$ consisting of eigenvectors of $\tat$ corresponding to eigenvalue $\lambda_1=2$. And
$$ \frac1{\sqrt2}Te_1=\frac1{\sqrt2}(g_1+g_2)=\frac1{\sqrt2}(1,1)=\Prn{\frac1{\sqrt2},\frac1{\sqrt2}} $$
is an orthonormal basis of $\rangsp{T}$. Note that $\dim{\rangsp{T}}=1$ and $\dim{\rangsp{T}}^\perp=1\geq 0=\dim{\wR}-\dim{\rangsp{T}}$.
Proposition PLRDC.2 Let $T\in\linmap{V}{W}$ and let $f_1,\dots,f_n$ denote an orthonormal basis of $V$ consisting of eigenvectors of $\tat$ corresponding to eigenvalues $\lambda_1,\dots,\lambda_n$ (existence given by the Spectral Theorem). And let $f_1,\dots,f_r$ denote the sublist that is an orthonormal basis of $\rangspb{\sqrttat}$ (existence given by PLRDC.1).
Define $S_1\in\linmapb{\rangspb{\sqrttat}}{\rangsp{T}}$ by
$$ S_1f_j\equiv\frac1{\sqrt{\lambda_j}}Tf_j\qd\text{for }j=1,\dots,r $$
And define $S_1’\in\linmapb{\rangspb{\sqrttat}}{\rangsp{T}}$ by
$$ S_1'\prn{\sqrttat v}\equiv Tv\qd\text{for all }v\in V $$
Then $S_1=S_1’$ and $\dnorm{S_1\alpha}_W=\dnorm{\alpha}_V$ for all $\alpha\in\rangspb{\sqrttat}$.
Proof PLRDC.1 shows that $\sqrt{\lambda_j}$, the eigenvalue of $\sqrttat$ corresponding to $f_j$, is positive for $j=1,\dots,r$. Since $f_1,\dots,f_r$ is a basis of $\rangspb{\sqrttat}$ (by PLRDC.1.A), then $S_1$ is a well-defined linear map (by 3.5).
We must show that $S_1’$ is a well-defined function. Suppose $v_1,v_2\in V$ are such that $\sqrttat v_1=\sqrttat v_2$. If it’s the case $Tv_1\neq Tv_2$, then $S_1’$ is not well-defined. But we have
$$ \dnorm{Tv_1-Tv_2}_W=\dnorm{T(v_1-v_2)}_W=\dnorm{\sqrttat(v_1-v_2)}_V=\dnorm{\sqrttat v_1-\sqrttat v_2}_V=0 $$
where the second equality follows from App.7. Hence, by 6.10(a), $Tv_1=Tv_2$.
$S_1’$ is also linear: Let $u_1,u_2\in\rangspb{\sqrttat}$. Then there exist $v_1,v_2\in V$ such that $u_1=\sqrttat v_1$ and $u_2=\sqrttat v_2$. Also let $\lambda\in\wF$. Then
$$\align{ S_1'(\lambda u_1+u_2) &= S_1'\prn{\lambda\sqrttat v_1+\sqrttat v_2} \\ &= S_1'\prn{\sqrttat(\lambda v_1)+\sqrttat v_2} \\ &= S_1'\prn{\sqrttat(\lambda v_1+v_2)} \\ &= T(\lambda v_1+v_2) \\ &= T(\lambda v_1)+Tv_2 \\ &= \lambda Tv_1+Tv_2 \\ &= \lambda S_1'\prn{\sqrttat v_1}+S_1'\prn{\sqrttat v_2} \\ &= \lambda S_1'u_1+S_1'u_2 }$$
Hence, for $j=1,\dots,r$, we have
$$ S_1'f_j = \frac{\sqrt{\lambda_j}}{\sqrt{\lambda_j}}S_1'f_j = \frac1{\sqrt{\lambda_j}}S_1'\prn{\sqrt{\lambda_j}f_j} = \frac1{\sqrt{\lambda_j}}S_1'\prn{\sqrttat f_j} = \frac1{\sqrt{\lambda_j}}Tf_j = S_1f_j $$
Since $f_1,\dots,f_r$ is a basis of $\rangspb{\sqrttat}$, then $S_1=S_1’$ (by 3.5 or App.14).
Lastly, let $\alpha\in\rangspb{\sqrttat}$. Then there exists $v\in V$ such that $\alpha=\sqrttat v$. Hence
$$ \dnorm{S_1\alpha}_W=\dnorm{S_1'\alpha}_W=\dnorm{S_1'\prn{\sqrttat v}}_W=\dnorm{Tv}_W=\dnorm{\sqrttat v}_V=\dnorm{\alpha}_V $$
where the next-to-last equality follows from App.7. $\wes$
Proposition PLRDC.3 - Polar Decomposition Let $T\in\linmap{V}{W}$.
If $\dim{W}\geq\dim{V}$, then there exist a subspace $U$ of $W$ with $\dim{U}=\dim{V}$, an isometry $S\in\linmap{V}{U}$, and an orthonormal basis $f\equiv f_1,\dots,f_n$ of $V$ consisting of eigenvectors of $\tat$ such that
$$ Tv=S\sqrttat v\qd\text{for all }v\in V \tag{PLRDC.3.1} $$
and
$$ Sf_j=\cases{\frac1{\sqrt{\lambda_j}}Tf_j&\text{for }j=1,\dots,\dim{\rangsp{T}}\\h_j&\text{for }j=\dim{\rangsp{T}}+1,\dots,n} \tag{PLRDC.3.2} $$
where $h_{\dim{\rangsp{T}}+1},\dots,h_n$ is any orthonormal list in $\rangsp{T}^\perp$ of length $n-\dim{\rangsp{T}}$.
If $\dim{W}\leq\dim{V}$, then there exist a subspace $U$ of $V$ with $\dim{U}=\dim{W}$ and an isometry $S\in\linmap{U}{W}$ such that
$$ Tv=\sqrttta Sv\qd\text{for all }v\in V $$
Proof First suppose that $\dim{W}\geq\dim{V}$.
Let $f_1,\dots,f_n$ denote an orthonormal basis of $V$ consisting of eigenvectors of $\tat$ corresponding to eigenvalues $\lambda_1,\dots,\lambda_n$ (existence given by the Spectral Theorem). And let $f_1,\dots,f_r$ denote the sublist that is an orthonormal basis of $\rangspb{\sqrttat}$ (existence given by PLRDC.1 - re-index if necessary) so that $\lambda_1,\dots,\lambda_r$ are positive. By PLRDC.1(E), we have $r=\dim{\rangsp{T}}$. Define $S_1\in\linmapb{\rangspb{\sqrttat}}{\rangsp{T}}$ by
$$ S_1f_j\equiv\frac1{\sqrt{\lambda_j}}Tf_j\qd\text{for }j=1,\dots,r $$
By PLRDC.1(B), $f_{r+1},\dots,f_n$ is an orthonormal basis of $\rangspb{\sqrttat}^\perp$. Since $\dim{W}\geq\dim{V}$, then PLRDC.1(F) implies that $\dim{\rangsp{T}}^\perp\geq n-r$. Let $h_{r+1},\dots,h_n$ be an orthonormal list in $\rangsp{T}^\perp$. Define $S_2\in\linmapb{\rangspb{\sqrttat}^\perp}{\span{h_{r+1},\dots,h_n}}$ by
$$ S_2f_j\equiv h_j\qd\text{for }j=r+1,\dots,n $$
Note that for any $\beta\in\rangspb{\sqrttat}^\perp$, we have $\beta=\sum_{j=r+1}^n\innprd{\beta}{f_j}f_j$ and
$$ \dnorm{S_2\beta}_W^2=\dnorm{S_2\Prngg{\sum_{j=r+1}^n\innprd{\beta}{f_j}f_j}}_W^2 =\dnorm{\sum_{j=r+1}^n\innprd{\beta}{f_j}S_2f_j}_W^2 =\dnorm{\sum_{j=r+1}^n\innprd{\beta}{f_j}h_j}_W^2 =\sum_{j=r+1}^n\normw{\innprd{\beta}{f_j}}^2 =\dnorm{\beta}_V^2 $$
The next-to-last equality follows from 6.25 and the last equality follows from 6.30. Put
$$ U \equiv \spanB{\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r,h_{r+1},\dots,h_n} \tag{PLRDC.3.3} $$
By PLRDC.1, $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r$ is an orthonormal basis of $\rangsp{T}$. And, by construction, $h_{r+1},\dots,h_n$ is an orthonormal list in $\rangsp{T}^\perp$. Hence $\frac1{\sqrt{\lambda_1}}Tf_1,\dots,\frac1{\sqrt{\lambda_r}}Tf_r,h_{r+1},\dots,h_n$ is orthonormal and hence linearly independent. Hence $\dim{U}=n=\dim{V}$.
By 6.47, $V=\rangspb{\sqrttat}\oplus\rangspb{\sqrttat}^\perp$. Hence any $v\in V$ can be uniquely decomposed as $v=\alpha+\beta$ where $\alpha\in\rangspb{\sqrttat}$ and $\beta\in\rangspb{\sqrttat}^\perp$. Define $S\in\linmap{V}{U}$ by
$$ Sv\equiv S_1\alpha+S_2\beta \tag{PLRDC.3.4} $$
Then
$$ \dnorm{Sv}_W^2=\dnorm{S_1\alpha+S_2\beta}_W^2=\dnorm{S_1\alpha}_W^2+\dnorm{S_2\beta}_W^2=\dnorm{\alpha}_V^2+\dnorm{\beta}_V^2=\dnorm{\alpha+\beta}_V^2=\dnorm{v}_V^2 $$
The second equality holds because $S_1\alpha\in\rangsp{T}$ and $S_2\beta\in\rangsp{T}^\perp$.
Next, define $S_1’$ as in PLRDC.2. Then, for any $v\in V$, we have
$$ S\sqrttat v = S\prn{\sqrttat v} = S_1\prn{\sqrttat v} = S_1'\prn{\sqrttat v} = Tv $$
The second equality holds because $\sqrttat v\in\rangspb{\sqrttat}$ and the third equality holds because $S_1=S_1’$ (by PLRDC.2). Also note that
$$ Sf_j=\cases{S_1f_j+S_2(0)&\text{for }j=1,\dots,r\\S_1(0)+S_2f_j&\text{for }j=r+1,\dots,n}=\cases{\frac1{\sqrt{\lambda_j}}Tf_j&\text{for }j=1,\dots,r\\h_j&\text{for }j=r+1,\dots,n}\in U $$
Now suppose that $\dim{W}\leq\dim{V}$. Since $\adjtT\in\linmap{W}{V}$, then there exist a subspace $U$ of $V$ with $\dim{U}=\dim{W}$ and an isometry $\adjt{S}\in\linmap{W}{U}$ such that
$$ \adjtT w=\adjt{S}\sqrt{\adjt{(\adjtT)}\adjtT}w=\adjt{S}\sqrttta w $$
for all $w\in W$. Hence, for all $v\in V$, we have
$$ Tv=\adjt{(\adjtT)}v=\adjt{\prn{\adjt{S}\sqrttta}}v=\adjt{\prn{\sqrttta}}\adjt{(\adjt{S})}v=\sqrttta Sv $$
By App.5, $S\in\linmap{U}{W}$ is also an isometry. $\wes$
We will briefly defer the matrix form of and an example of Polar Decomposition. First we will extend Axler’s Spectral Theorems 7.24 (complex) and 7.29 (real). Then we will present and prove SVD. Then we’ll return to Polar Decomposition.
Proposition SPECT.1 - Real (Complex) Spectral Decomposition Let $T\wiov$. Then $T$ is self-adjoint (normal) if and only if $V$ has an orthonormal basis $f$ consisting of eigenvectors of $T$ such that, for any orthonormal basis $e$ of $V$, we have
$$ \mtrxof{T,e}=\mtrxof{I,f,e}\mtrxof{T,f}\adjt{\mtrxof{I,f,e}} \tag{SPECT.1.1} $$
where $\mtrxof{T,f}$ is diagonal and $\mtrxof{I,f,e}$ has orthonormal columns and rows.
Note If $\mtrxof{T,f}$ is diagonal, then 5.32 implies that the eigenvalues of $T$ are precisely the entries on the diagonal of $\mtrxof{T,f}$. And App.9 implies that each eigenvalue $\lambda$ of $T$ appears on the diagonal precisely $\dim{\eignsp{\lambda}{T}}$ times.
Proof Suppose $T$ is self-adjoint (normal). By 7.24(c) or 7.29(c), $T$ has a diagonal matrix with respect to some orthonormal basis $f$ of $V$. Hence, for any orthonormal basis $e$ of $V$, we have
$$\align{ \mtrxof{T,e} &= \mtrxof{I,f,e}\mtrxof{T,f}\mtrxof{I,e,f}\tag{by App.6} \\ &= \mtrxof{I,f,e}\mtrxof{T,f}\mtrxof{\adjt{I},e,f}\tag{by 7.6(d)} \\ &= \mtrxof{I,f,e}\mtrxof{T,f}\adjt{\mtrxof{I,f,e}}\tag{by App.4} }$$
Note that $\dnorm{Iv}=\dnorm{v}$. Hence $I\wiov$ is an isometry and App.25 implies that $\mtrxof{I,f,e}$ has orthonormal columns and rows.
Conversely, suppose that $V$ has an orthonormal basis $f$ consisting of eigenvectors of $T$ such that, for any orthonormal basis $e$ of $V$, we have
$$ \mtrxof{T,e}=\mtrxof{I,f,e}\mtrxof{T,f}\adjt{\mtrxof{I,f,e}} $$
and $\mtrxof{T,f}$ is diagonal. Hence, by 7.24(c) or 7.29(c), $T$ is self-adjoint (normal).
$\wes$
Proposition SVD.1 Singular Value Decomposition Let $T\in\linmap{V}{W}$, let $e\equiv e_1,\dots,e_n$ denote any orthonormal basis of $V$, and let $g\equiv g_1,\dots,g_m$ denote an orthonormal basis of $W$.
If $\dim{W}\geq\dim{V}$, then (A)-(G) hold:
(A) There exist a subspace $U$ of $W$ with $\dim{U}=\dim{V}$, an isometry $S\in\linmap{V}{U}$, and an orthonormal basis $f$ of $V$ such that
$$ \mtrxof{T,e,g}=\mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \tag{SVD.1.1} $$
where $\mtrxofb{\sqrttat,f}$ is diagonal and
$$ \mtrxofb{\sqrttat,f}^2=\pmtrx{\sqrt{\lambda_1}&&\\&\ddots&\\&&\sqrt{\lambda_n}}^2 =\pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n}=\mtrxof{\tat,f} $$
(B) The square roots of the eigenvalues of $\tat$ are precisely the diagonal entries of $\mtrxofb{\sqrttat,f}$, with each eigenvalue $\lambda_j$ repeated $\dim{\eignsp{\lambda_j}{\tat}}$ times.
(C) The columns of $\mtrxof{S,f,g}$ and $\mtrxof{I,f,e}$ are orthonormal with respect to $\innprddt_{\wF^m}$ and $\innprddt_{\wF^n}$.
(D) The singular values of $T$ are precisely the square roots of the diagonal entries of $\mtrxof{\tat,f}$, with each singular value $\sqrt{\lambda_j}$ repeated $\dim{\eignsp{\lambda_j}{\tat}}$ times.
(E) The columns of $\mtrxof{I,f,e}$ are eigenvectors of $\mtrxof{\tat,e}$. That is, $\mtrxof{f_j,e}$ is an eigenvector of $\mtrxof{\tat,e}$ corresponding to eigenvalue $\lambda_j$.
(F) The columns of $\mtrxof{S,f,g}$ are eigenvectors of $\mtrxof{\tta,g}$. That is, $\mtrxof{Sf_j,g}$ is an eigenvector of $\mtrxof{\tta,g}$ corresponding to eigenvalue $\lambda_j$.
(G) $\mtrxof{T,e,g}=\sum_{j=1}^{\dim{\rangsp{T}}}\sqrt{\lambda_j}\mtrxof{Sf_j,g}\adjt{\mtrxof{f_j,e}}$
(H) If $\dim{W}\leq\dim{V}$, then there exist a subspace $U$ of $V$ with $\dim{U}=\dim{W}$, an isometry $S\in\linmap{U}{W}$, and an orthonormal basis $f$ of $W$ such that
$$ \mtrxof{T,e,g} = \mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\adjt{\mtrxof{\adjt{S},f,e}} \tag{SVD.1.2} $$
Proof of (A) Note that $\tat$ is a positive operator:
$$ \adjt{(\tat)}=\adjtT\adjt{(\adjtT)}=\tat $$
And for any $v\in V$:
$$ \innprd{\tat v}{v}_V=\innprd{Tv}{\adjt{(\adjtT)}v}_W=\innprd{Tv}{Tv}_W=\dnorm{Tv}_W^2\geq0 $$
Then the Spectral Theorem (SPECT.1) gives an orthonormal basis $f\equiv f_1,\dots,f_n$ of $V$ consisting of eigenvectors of $\tat$ corresponding to eigenvalues $\lambda_1,\dots,\lambda_n$ so that $\mtrxof{\tat,f}$ is diagonal and
$$ \mtrxof{\tat,e}=\mtrxof{I,f,e}\mtrxof{\tat,f}\adjt{\mtrxof{I,f,e}} $$
Then App.2 gives that $f_1,\dots,f_n$ consists of eigenvectors of $\sqrttat$ corresponding to eigenvalues $\sqrt{\lambda_1},\dots,\sqrt{\lambda_n}$ so that $\mtrxofb{\sqrttat,f}$ is diagonal and
$$ \mtrxofb{\sqrttat,e}=\mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} $$
Define $U$ as in PLRDC.3.3 and define $S\in\linmap{V}{U}$ as in PLRDC.3.4. Then $S\sqrttat v=Tv$ for all $v\in V$. In particular, $S\sqrttat e_j=Te_j$ for $j=1,\dots,n$. Hence
$$\align{ \mtrxof{T,e,g} &= \mtrxofb{S\sqrttat,e,g}\tag{by PLRDC.3} \\ &= \mtrxof{S,e,g}\mtrxofb{\sqrttat,e,e}\tag{by App.11} \\ &= \mtrxof{SI,e,g}\mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\tag{by SPECT.1} \\ &= \mtrxof{S,f,g}\mtrxof{I,e,f}\mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\tag{by App.11} \\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\tag{by App.12} }$$
Proof of (B) 5.32 implies that the eigenvalues of $\tat$ are precisely the diagonal entries of $\mtrxof{\tat,f}$. And App.9 implies that each eigenvalue $\lambda_j$ is repeated $\dim{\eignsp{\lambda_j}{\tat}}$ times on the diagonal. And App.2 shows that the square roots of these eigenvalues are precisely the diagonal entries of $\mtrxofb{\sqrttat,f}$.
Proof of (C) Since $S$ is an isometry, then $Sf_1,\dots,Sf_n$ is orthonormal (by App.5). Also note that 6.30 gives
$$ Sf_k=\sum_{i=1}^m\innprd{Sf_k}{g_i}_Wg_i $$
Then
$$\align{ \mtrxof{S,f,g} &= \pmtrx{\mtrxof{S,f,g}_{:,1}&\dotsb&\mtrxof{S,f,g}_{:,n}} \\ &= \pmtrx{\mtrxof{Sf_1,g}&\dotsb&\mtrxof{Sf_n,g}} \\ &= \pmtrx{\innprd{Sf_1}{g_1}_W&\dotsb&\innprd{Sf_n}{g_1}_W\\\vdots&\ddots&\vdots\\\innprd{Sf_1}{g_m}_W&\dotsb&\innprd{Sf_n}{g_m}_W} \\ }$$
and
$$\align{ \innprdbg{\mtrxof{S,f,g}_{:,j}}{\mtrxof{S,f,g}_{:,k}}_{\wF^m} &= \sum_{i=1}^m\innprd{Sf_j}{g_i}_W\cj{\innprd{Sf_k}{g_i}_W} \\ &= \sum_{i=1}^m\innprdbg{Sf_j}{\innprd{Sf_k}{g_i}_Wg_i}_W \\ &= \innprdBgg{Sf_j}{\sum_{i=1}^m\innprd{Sf_k}{g_i}_Wg_i}_W \\ &= \innprd{Sf_j}{Sf_k}_W\tag{by 6.30} \\ &= \cases{1&j=k\\0&j\neq k} }$$
Hence the columns of $\mtrxof{S,f,g}$ are orthonormal with respect to $\innprddt_{\wF^m}$. Since $If_1,\dots,If_n$ is orthonormal, the proof is similar that the columns of $\mtrxof{I,f,e}$ are orthonormal with respect to $\innprddt_{\wF^n}$.
Proof of (D) This follows from App.3.
Proof of (E) Note that $f_j$ was chosen to be an eigenvector of $\tat$ corresponding to eigenvalue $\lambda_j$. Hence $\tat f_j=\lambda_jf_j$ and
$$ \mtrxof{\tat,e}\mtrxof{f_j,e}=\mtrxof{\tat f_j,e}=\mtrxof{\lambda_jf_j,e}=\lambda_j\mtrxof{f_j,e} $$
Alternatively, note that
$$ \mtrxofb{\sqrttat,f}\mtrxofb{\sqrttat,f}=\pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} $$
And let $\epsilon_1,\dots,\epsilon_n$ denote the standard basis in $\wR^n$. Then
$$\align{ \mtrxof{\tat,e}\mtrxof{f_j,e} &= \mtrxof{\adjtT,g,e}\mtrxof{T,e,g}\mtrxof{f_j,e} \\\\ &= \adjt{\mtrxof{T,e,g}}\mtrxof{T,e,g}\mtrxof{f_j,e} \\\\ &= \adjt{\sbr{\mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}}}\mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\mtrxof{f_j,e} \\\\ &= \adjt{\prn{\adjt{\mtrxof{I,f,e}}}}\adjt{\mtrxofb{\sqrttat,f}}\adjt{\mtrxof{S,f,e}}\mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\mtrxof{f_j,e} \\\\ &= \mtrxof{I,f,e}\mtrxofb{\adjt{\prn{\sqrttat}},f}\mtrxof{\adjt{S},e,f}\mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\mtrxof{f_j,e} \\\\ &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\mtrxof{\adjt{S}S,f,f}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\mtrxof{f_j,e} \\\\ &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\mtrxof{I,f,f}\mtrxofb{\sqrttat,f}\mtrxof{\adjt{I},e,f}\mtrxof{f_j,e} \\\\ &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\mtrxofb{\sqrttat,f}\mtrxof{I,e,f}\mtrxof{f_j,e} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\innprd{e_1}{f_1}&\dotsb&\innprd{e_n}{f_1}\\\vdots&\ddots&\vdots\\\innprd{e_1}{f_n}&\dotsb&\innprd{e_n}{f_n}} \pmtrx{\innprd{f_j}{e_1}\\\vdots\\\innprd{f_j}{e_n}} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\sum_{k=1}^n\innprd{e_k}{f_1}\innprd{f_j}{e_k}\\\vdots\\\sum_{k=1}^n\innprd{e_k}{f_n}\innprd{f_j}{e_k}} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\sum_{k=1}^n\innprdbg{\innprd{f_j}{e_k}e_k}{f_1}\\\vdots\\\sum_{k=1}^n\innprdbg{\innprd{f_j}{e_k}e_k}{f_n}} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\innprdBg{\sum_{k=1}^n\innprd{f_j}{e_k}e_k}{f_1}\\\vdots\\\innprdBg{\sum_{k=1}^n\innprd{f_j}{e_k}e_k}{f_n}} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\innprd{f_j}{f_1}\\\vdots\\\innprd{f_j}{f_n}} \\\\ &= \pmtrx{\innprd{f_1}{e_1}&\dotsb&\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\innprd{f_1}{e_n}&\dotsb&\innprd{f_n}{e_n}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \epsilon_j \\\\ &= \pmtrx{\lambda_1\innprd{f_1}{e_1}&\dotsb&\lambda_n\innprd{f_n}{e_1}\\\vdots&\ddots&\vdots\\\lambda_1\innprd{f_1}{e_n}&\dotsb&\lambda_n\innprd{f_n}{e_n}} \epsilon_j \\\\ &= \pmtrx{\lambda_j\innprd{f_j}{e_1}\\\vdots\\\lambda_j\innprd{f_j}{e_n}} \\\\ &= \lambda_j\pmtrx{\innprd{f_j}{e_1}\\\vdots\\\innprd{f_j}{e_n}} \\\\ &= \lambda_j\mtrxof{f_j,e} }$$
Proof of (F) By PLRDC.3.2, for $j=1,\dots,r$, we have
$$ \tta Sf_j=\tta\frac1{\sqrt{\lambda_j}}Tf_j=\frac1{\sqrt{\lambda_j}}\tta Tf_j=\frac1{\sqrt{\lambda_j}}T(\tat f_j)=\frac1{\sqrt{\lambda_j}}T(\lambda_jf_j)=\lambda_j\frac1{\sqrt{\lambda_j}}Tf_j=\lambda_jSf_j $$
and, for $j=r+1,\dots,n$, we have
$$ \tta Sf_j=\tta h_j=T(0)=0=0Sf_j=\lambda_jSf_j $$
The second equality follows from PLRDC.1(G). Hence
$$ \mtrxof{\tta,g}\mtrxof{Sf_j,g}=\mtrxof{\tta Sf_j,g}=\mtrxof{\lambda_jSf_j,g}=\lambda_j\mtrxof{Sf_j,g} $$
Alternatively, let $\epsilon_1,\dots,\epsilon_n$ denote the standard basis in $\wR^n$. Then
$$\align{ \mtrxof{\tta,g}\mtrxof{Sf_j,g} &= \mtrxof{T,e,g}\mtrxof{\adjtT,g,e}\mtrxof{Sf_j,g} \\\\ &= \mtrxof{T,e,g}\adjt{\mtrxof{T,e,g}}\mtrxof{Sf_j,g} \\\\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}\adjt{\sbr{\mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}}}\mtrxof{Sf_j,g} \\\\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\mtrxof{\adjt{I},e,f}\adjt{\prn{\adjt{\mtrxof{I,f,e}}}}\adjt{\mtrxofb{\sqrttat,f}}\adjt{\mtrxof{S,f,g}}\mtrxof{Sf_j,g} \\\\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\mtrxof{I,e,f}\mtrxof{I,f,e}\mtrxofb{\adjt{\prn{\sqrttat}},f}\mtrxof{\adjt{S},g,f}\mtrxof{Sf_j,g} \\\\ &= \pmtrx{\mtrxof{S,f,g}_{:,1}&\dotsb&\mtrxof{S,f,g}_{:,n}}\mtrxofb{\sqrttat,f}\mtrxofb{\sqrttat,f}\mtrxof{\adjt{S}Sf_j,f} \\\\ &= \pmtrx{\mtrxof{Sf_1,g}&\dotsb&\mtrxof{Sf_n,g}}\mtrxofb{\sqrttat,f}\mtrxofb{\sqrttat,f}\mtrxof{f_j,f} \\\\ &= \pmtrx{\innprd{Sf_1}{g_1}&\dotsb&\innprd{Sf_n}{g_1}\\\vdots&\ddots&\vdots\\\innprd{Sf_1}{g_m}&\dotsb&\innprd{Sf_n}{g_m}} \pmtrx{\lambda_1&&\\&\ddots&\\&&\lambda_n} \pmtrx{\innprd{f_j}{f_1}\\\vdots\\\innprd{f_j}{f_n}} \\\\ &= \pmtrx{\lambda_1\innprd{Sf_1}{g_1}&\dotsb&\lambda_n\innprd{Sf_n}{g_1}\\\vdots&\ddots&\vdots\\\lambda_1\innprd{Sf_1}{g_m}&\dotsb&\lambda_n\innprd{Sf_n}{g_m}} \epsilon_j \\\\ &= \pmtrx{\lambda_j\innprd{Sf_j}{g_1}\\\vdots\\\lambda_j\innprd{Sf_j}{g_m}} \\\\ &= \lambda_j\pmtrx{\innprd{Sf_j}{g_1}\\\vdots\\\innprd{Sf_j}{g_m}} \\\\ &= \lambda_j\mtrxof{Sf_j,g} }$$
Proof of (G)
$$\align{ \mtrxof{T,e,g} &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\mtrxof{\adjt{I},e,f} \\ &= \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\mtrxof{I,e,f} \\\\ &= \pmtrx{\innprd{Sf_1}{g_1}&\dotsb&\innprd{Sf_n}{g_1}\\\vdots&\ddots&\vdots\\\innprd{Sf_1}{g_m}&\dotsb&\innprd{Sf_n}{g_m}} \pmtrx{\sqrt{\lambda_1}&&\\&\ddots&\\&&\sqrt{\lambda_n}} \pmtrx{\innprd{e_1}{f_1}&\dotsb&\innprd{e_n}{f_1}\\\vdots&\ddots&\vdots\\\innprd{e_1}{f_n}&\dotsb&\innprd{e_n}{f_n}} \\\\ &= \pmtrx{\innprd{Sf_1}{g_1}&\dotsb&\innprd{Sf_n}{g_1}\\\vdots&\ddots&\vdots\\\innprd{Sf_1}{g_m}&\dotsb&\innprd{Sf_n}{g_m}} \pmtrx{\sqrt{\lambda_1}\innprd{e_1}{f_1}&\dotsb&\sqrt{\lambda_1}\innprd{e_n}{f_1}\\\vdots&\ddots&\vdots\\\sqrt{\lambda_n}\innprd{e_1}{f_n}&\dotsb&\sqrt{\lambda_n}\innprd{e_n}{f_n}} \\\\ &= \pmtrx{\sum_{j=1}^n\sqrt{\lambda_j}\innprd{Sf_j}{g_1}\innprd{e_1}{f_j}&\dotsb&\sum_{j=1}^n\sqrt{\lambda_j}\innprd{Sf_j}{g_1}\innprd{e_n}{f_j}\\\vdots&\ddots&\vdots\\\sum_{j=1}^n\sqrt{\lambda_j}\innprd{Sf_j}{g_m}\innprd{e_1}{f_j}&\dotsb&\sum_{j=1}^n\sqrt{\lambda_j}\innprd{Sf_j}{g_m}\innprd{e_n}{f_j}} \\\\ &= \sum_{j=1}^n\pmtrx{\sqrt{\lambda_j}\innprd{Sf_j}{g_1}\innprd{e_1}{f_j}&\dotsb&\sqrt{\lambda_j}\innprd{Sf_j}{g_1}\innprd{e_n}{f_j}\\\vdots&\ddots&\vdots\\\sqrt{\lambda_j}\innprd{Sf_j}{g_m}\innprd{e_1}{f_j}&\dotsb&\sqrt{\lambda_j}\innprd{Sf_j}{g_m}\innprd{e_n}{f_j}} \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\pmtrx{\innprd{Sf_j}{g_1}\innprd{e_1}{f_j}&\dotsb&\innprd{Sf_j}{g_1}\innprd{e_n}{f_j}\\\vdots&\ddots&\vdots\\\innprd{Sf_j}{g_m}\innprd{e_1}{f_j}&\dotsb&\innprd{Sf_j}{g_m}\innprd{e_n}{f_j}} \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\pmtrx{\innprd{Sf_j}{g_1}\\\vdots\\\innprd{Sf_j}{g_m}} \pmtrx{\innprd{e_1}{f_j}&\dotsb&\innprd{e_n}{f_j}} \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\mtrxof{Sf_j,g}\pmtrx{\cj{\innprd{f_j}{e_1}}&\dotsb&\cj{\innprd{f_j}{e_n}}} \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\mtrxof{Sf_j,g}\pmtrx{\cj{\innprd{f_j}{e_1}}\\\vdots\\\cj{\innprd{f_j}{e_n}}}^t \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\mtrxof{Sf_j,g}\adjt{\pmtrx{\innprd{f_j}{e_1}\\\vdots\\\innprd{f_j}{e_n}}} \\\\ &= \sum_{j=1}^n\sqrt{\lambda_j}\mtrxof{Sf_j,g}\adjt{\mtrxof{f_j,e}} \\ &= \sum_{j=1}^{\dim{\rangsp{T}}}\sqrt{\lambda_j}\mtrxof{Sf_j,g}\adjt{\mtrxof{f_j,e}} }$$
where the last equality follows because PLRDC.1(G) gives $\lambda_j=0$ for $j=\dim{\rangsp{T}}+1,\dots,n$.
Proof of (H) Note that $\tta$ is a positive operator:
$$ \adjt{(\tta)}=\adjt{(\adjtT)}\adjtT=\tta $$
And for any $w\in W$:
$$ \innprd{\tta w}{w}_W=\innprd{\adjtT w}{\adjtT w}_V=\dnorm{\adjtT w}_V^2\geq0 $$
Hence, by 7.36 and 7.44, $\sqrttta$ is the unique positive square root of $\tta$. Since $\sqrttta$ is positive, it’s also self-adjoint. Then SPECT.1 gives an orthonormal basis $f$ of $W$ such that $\mtrxofb{\sqrttta,f}$ is diagonal and
$$ \mtrxofb{\sqrttta,g}=\mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\adjt{\mtrxof{I,f,g}} $$
Hence
$$\align{ \mtrxof{T,e,g} &= \mtrxofb{\sqrttta S,e,g}\tag{by Polar Decomposition PLRDC.3} \\ &= \mtrxofb{\sqrttta,g,g}\mtrxof{S,e,g}\tag{by App.11} \\ &= \mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\adjt{\mtrxof{I,f,g}}\mtrxof{IS,e,g}\tag{by SPECT.1} \\ &= \mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\mtrxof{\adjt{I},g,f}\mtrxof{I,f,g}\mtrxof{S,e,f}\tag{by App.11} \\ &= \mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\mtrxof{I,g,f}\mtrxof{I,f,g}\adjt{\mtrxof{\adjt{S},f,e}}\tag{by App.4} \\ &= \mtrxof{I,f,g}\mtrxofb{\sqrttta,f}\adjt{\mtrxof{\adjt{S},f,e}}\tag{by App.12} }$$
$\wes$
Example SVD.2 Find the SVD of
$$ \mtrxof{T,e}\equiv\pmtrx{5&5\\-1&7} $$
where $e\equiv e_1,e_2$ is the standard basis of $\wR^2$. Note that
$$\align{ &Te_1=5e_1-1e_2=(5,-1) \\ &Te_2=5e_1+7e_2=(5,7) }$$
or
$$\align{ T(x,y) = T(xe_1+ye_2) = xTe_1+yTe_2 = x(5,-1)+y(5,7) = (5x,-x)+(5y,7y) = (5x+5y,-x+7y) \tag{SVD.2.0} }$$
Hence
$$\align{ \tat e_1 &= \adjtT(Te_1) \\ &= \innprd{Te_1}{Te_1}e_1+\innprd{Te_1}{Te_2}e_2 \\ &= \innprd{(5,-1)}{(5,-1)}e_1+\innprd{(5,-1)}{(5,7)}e_2 \\ &= (25+1)e_1+(25-7)e_2 \\ &= 26e_1+18e_2 }$$
and
$$\align{ \tat e_2 &= \adjtT(Te_2) \\ &= \innprd{Te_2}{Te_1}e_1+\innprd{Te_2}{Te_2}e_2 \\ &= \innprd{(5,7)}{(5,-1)}e_1+\innprd{(5,7)}{(5,7)}e_2 \\ &= (25-7)e_1+(25+49)e_2 \\ &= 18e_1+74e_2 }$$
Hence
$$\align{ \tat(x,y) &= \tat(xe_1+ye_2) \\ &= x\tat e_1+y\tat e_2 \\ &= x(26e_1+18e_2)+y(18e_1+74e_2) \\ &= x26e_1+x18e_2+y18e_1+y74e_2 \\ &= x26e_1+y18e_1+x18e_2+y74e_2 \\ &= (x26+y18)e_1+(x18+y74)e_2 \\ &= (x26+y18,x18+y74) \\ &= (26x+18y,18x+74y) \tag{SVD.2.1} }$$
Let’s find the eigenvalues of $\tat$. Then we’ll find corresponding eigenvectors. Then we’ll apply Gram-Schmidt to get an orthonormal eigenbasis of $\wR^2$ corresponding to $\tat$. Actually, since $\tat$ is self-adjoint, 7.22 and App.23 imply that it’s not necessary to perform the full Gram-Schmidt; we just need to normalize each of the eigenvectors.
Note that 7.13 implies that $\tat$ has real eigenvalues. The eigenpair equation is
$$ (\lambda x,\lambda y)=\lambda(x,y)=\tat(x,y)=(26x+18y,18x+74y) $$
This becomes the system
$$\align{ &26x+18y=\lambda x \\ &18x+74y=\lambda y }$$
If $x=0$, then $18y=0$ and $y=0$. And if $y=0$, then $18x=0$ and $x=0$. Since eigenvectors cannot be zero, then it must be that $x\neq0$ and $y\neq0$. Also note that
$$ 18y=\lambda x-26x=(\lambda-26)x \dq\implies\dq y=\frac{\lambda-26}{18}x \tag{SVD.2.2} $$
and
$$ 18x=\lambda y-74y=(\lambda-74)y=(\lambda-74)\frac{\lambda-26}{18}x $$
or
$$ 18^2=(\lambda-74)(\lambda-26)=\lambda^2-26\lambda-74\lambda+74\cdot26 $$
or
$$ 0=\lambda^2-100\lambda+74\cdot26-18^2 $$
def quad_form(a=1,b=1,c=1):
disc = b**2-4*a*c
if disc < 0:
raise ValueError('The discriminant b^2-4ac={} is less than zero.'.format(disc))
p1 = -b/(2*a)
p2 = np.sqrt(disc)/(2*a)
return (p1+p2,p1-p2)
quad_form(a=1,b=-100,c=74*26-18**2)
(80.0, 20.0)
def compute_MTaTe(MTe):
MTae=MTe.conj().T
MTaTe=np.matmul(MTae,MTe)
return MTaTe
MTe=np.array([[5,5],[-1,7]])
MTaTe=compute_MTaTe(MTe)
MTaTe
array([[26, 18],
[18, 74]])
def real_eigns_2x2(npa=np.array([[1,0],[0,1]])):
b = -(npa[0,0]+npa[1,1])
c = npa[0,0]*npa[1,1]-npa[0,1]*npa[1,0]
eignvals = quad_form(a=1,b=b,c=c)
y0 = (eignvals[0]-npa[0,0])/npa[0,1] # by SVD.2.2
y1 = (eignvals[1]-npa[0,0])/npa[0,1] # by SVD.2.2
evctr0 = np.array([1,y0])
evctr1 = np.array([1,y1])
return (eignvals,evctr0,evctr1)
# by 7.13, MTaTe has real eigenvalues
eigvals,v1,v2=real_eigns_2x2(MTaTe)
eigvals
(80.0, 20.0)
v1
array([ 1., 3.])
v2
array([ 1. , -0.33333333])
Let’s verify these. From SVD.2.1, we have
$$\align{ &\tat(1,3) = (26\cdot1+18\cdot3,18\cdot1+74\cdot3) = (26+54,18+222) = (80,240) = 80(1,3) \\\\ &\tat\Prn{1,-\frac13} = \Prn{26\cdot1-18\cdot\frac13,18\cdot1-74\cdot\frac13} = \Prn{26-6,\frac{54-74}3} = \Prn{20,-\frac{20}3} = 20\Prn{1,-\frac13} }$$
Next we normalize this eigenbasis:
$$\align{ &f_1\equiv\frac{(1,3)}{\dnorm{(1,3)}} = \frac{(1,3)}{\sqrt{1+9}} = \frac1{\sqrt{10}}(1,3) \\\\ &f_2\equiv\frac{\prn{1,-\frac13}}{\dnorm{\prn{1,-\frac13}}} = \frac{\prn{1,-\frac13}}{\sqrt{1+\frac19}} = \frac{\prn{1,-\frac13}}{\sqrt{\frac{10}{9}}} = \frac{\prn{1,-\frac13}}{\frac{\sqrt{10}}3} = \frac{\prn{3,-1}}{\sqrt{10}} = \frac1{\sqrt{10}}(3,-1) }$$
or
def Rn_innprd(u,v):
if len(u) != len(v):
raise ValueError('Rn_innprd: vector lengths not equal: {} != {}'.format(len(u),len(v)))
return np.sum(u[i]*v[i] for i in range(len(u)))
Rn_norm=lambda v: np.sqrt(Rn_innprd(v,v))
def gram_schmidt(lin_ind_lst):
v0 = lin_ind_lst[0]
e0 = v0 / Rn_norm(v0)
ol = [e0]
for i in range(1,len(lin_ind_lst)):
vi = lin_ind_lst[i]
wi = vi - np.sum(Rn_innprd(vi,ol[j]) * ol[j] for j in range(i))
ei = wi / Rn_norm(wi)
ol.append(ei)
return ol
# quick check:
v = [np.array([41,41]),np.array([-17,0])]
gram_schmidt(v)
[array([ 0.70710678, 0.70710678]), array([-0.70710678, 0.70710678])]
v = [v1,v2]
f = gram_schmidt(v)
f
[array([ 0.31622777, 0.9486833 ]), array([ 0.9486833 , -0.31622777])]
def normalize(lst):
nl = []
for i in range(len(lst)):
vi = lst[i]
ni = vi / Rn_norm(vi)
nl.append(ni)
return nl
# normalized eigenbase agrees with gram-schmidt applied to this eigenbase:
normalize(v)
[array([ 0.31622777, 0.9486833 ]), array([ 0.9486833 , -0.31622777])]
# check against our manually computed f1 and f2:
mcf1=(1/np.sqrt(10))*np.array([1,3])
mcf2=(1/np.sqrt(10))*np.array([3,-1])
mcf1,mcf2
(array([ 0.31622777, 0.9486833 ]), array([ 0.9486833 , -0.31622777]))
By App.2, $\sqrttat$ is defined by
$$ \sqrttat f_1 = \sqrt{80}f_1 \dq\dq \sqrttat f_2 = \sqrt{20}f_2 $$
Define $f\equiv f_1,f_2$. Then $\mtrxofb{\sqrttat,f}$ is diagonal and the eigenvalues of $\sqrttat$ are precisely the entries on the diagonal:
$$ \mtrxofb{\sqrttat,f}=\pmtrx{\sqrt{80}&0\\0&\sqrt{20}} $$
We see that the list $\sqrttat f_1,\sqrttat f_2$ is orthogonal. Hence $\sqrttat f_1,\sqrttat f_2$ is linearly independent and hence is a basis of $\rangspb{\sqrttat}=\wR^2$.
Now define $S\in\oper{\wR^2}$ by
$$ S\prn{\sqrttat f_1} \equiv Tf_1 \dq\dq S\prn{\sqrttat f_2} \equiv Tf_2 \tag{SVD.2.3} $$
7.46 and 7.47 imply that $S$ is an isometry. Note that
$$\align{ \sqrt{80}Sf_1 &= S\prn{\sqrt{80}f_1} \\ &= S\prn{\sqrttat f_1} \\ &= Tf_1 \\ &= T\Prn{\frac1{\sqrt{10}}(1,3)} \\ &= \frac1{\sqrt{10}}T(1,3) \\ &= \frac1{\sqrt{10}}(5\cdot1+5\cdot3,-1+7\cdot3) \\ &= \frac1{\sqrt{10}}(20,20) }$$
and
$$ Sf_1 = \frac1{\sqrt{80}}\frac1{\sqrt{10}}(20,20) = \frac1{\sqrt{800}}\prn{\sqrt{400},\sqrt{400}}=\Prn{\frac1{\sqrt2},\frac1{\sqrt2}} = \frac1{\sqrt2}e_1+\frac1{\sqrt2}e_2 $$
Similarly
$$\align{ \sqrt{20}Sf_2 &= S\prn{\sqrt{20}f_2} \\ &= S\prn{\sqrttat f_2} \\ &= Tf_2 \\ &= T\Prn{\frac1{\sqrt{10}}(3,-1)} \\ &= \frac1{\sqrt{10}}T(3,-1) \\ &= \frac1{\sqrt{10}}(5\cdot3-5\cdot1,-3-7\cdot1) \\ &= \frac1{\sqrt{10}}(10,-10) }$$
and
$$ Sf_2 = \frac1{\sqrt{20}}\frac1{\sqrt{10}}(10,-10) = \frac1{\sqrt{200}}\prn{\sqrt{100},-\sqrt{100}}=\Prn{\frac1{\sqrt2},-\frac1{\sqrt2}} = \frac1{\sqrt2}e_1-\frac1{\sqrt2}e_2 $$
and
$$\align{ \mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} &= \pmtrx{\frac1{\sqrt2}&\frac1{\sqrt2}\\\frac1{\sqrt2}&-\frac1{\sqrt2}}\pmtrx{\sqrt{80}&0\\0&\sqrt{20}}\adjt{\pmtrx{\frac{1}{\sqrt{10}}&\frac{3}{\sqrt{10}}\\\frac{3}{\sqrt{10}}&-\frac{1}{\sqrt{10}}}} \\\\ &= \pmtrx{\frac{\sqrt{80}}{\sqrt{2}}&\frac{\sqrt{20}}{\sqrt{2}}\\\frac{\sqrt{80}}{\sqrt{2}}&-\frac{\sqrt{20}}{\sqrt{2}}}\pmtrx{\frac{1}{\sqrt{10}}&\frac{3}{\sqrt{10}}\\\frac{3}{\sqrt{10}}&-\frac{1}{\sqrt{10}}} \\\\ &= \pmtrx{\frac{\sqrt{80}}{\sqrt{2}\sqrt{10}}+\frac{3\sqrt{20}}{\sqrt{2}\sqrt{10}} & \frac{3\sqrt{80}}{\sqrt{2}\sqrt{10}}-\frac{\sqrt{20}}{\sqrt{2}\sqrt{10}} \\ \frac{\sqrt{80}}{\sqrt{2}\sqrt{10}}-\frac{3\sqrt{20}}{\sqrt{2}\sqrt{10}} & \frac{3\sqrt{80}}{\sqrt{2}\sqrt{10}}+\frac{\sqrt{20}}{\sqrt{2}\sqrt{10}} } \\\\ &= \pmtrx{\sqrt{\frac{80}{20}}+3\sqrt{\frac{20}{20}}&3\sqrt{\frac{80}{20}}-\sqrt{\frac{20}{20}} \\ \sqrt{\frac{80}{20}}-3\sqrt{\frac{20}{20}}&3\sqrt{\frac{80}{20}}+\sqrt{\frac{20}{20}} } \\\\ &= \pmtrx{2+3&3\cdot2-1\\2-3&3\cdot2+1} \\\\ &= \pmtrx{5&5\\-1&7} \\\\ &= \mtrxof{T,e} }$$
In SVD.2.3, we defined $S\in\oper{\wR^2}$ by
$$ S\prn{\sqrttat f_1} \equiv Tf_1 \dq\dq S\prn{\sqrttat f_2} \equiv Tf_2 $$
But PLRDC.2 gives an equivalent and slightly more efficient definition:
$$ Sf_1\equiv\frac1{\sqrt{\lambda_1}}Tf_1 \dq\dq Sf_2\equiv\frac1{\sqrt{\lambda_2}}Tf_2 $$
Then
$$\align{ Sf_1 &= \frac1{\sqrt{80}}Tf_1 \\ &= \frac1{\sqrt{80}}T\Prn{\frac1{\sqrt{10}}(1,3)} \\ &= \frac1{\sqrt{80}}\frac1{\sqrt{10}}T(1,3) \\ &= \frac1{\sqrt{800}}(5\cdot1+5\cdot3,-1+7\cdot3) \\ &= \frac1{\sqrt{800}}(20,20) \\ &= \frac1{\sqrt{800}}\prn{\sqrt{400},\sqrt{400}} \\ &= \Prn{\frac1{\sqrt2},\frac1{\sqrt2}} \\ &= \frac1{\sqrt2}e_1+\frac1{\sqrt2}e_2 }$$
and similarly for $Sf_2$.
$\wes$
Example SVD.3 Find the SVD of
$$ \mtrxof{T,e,g}\equiv\pmtrx{5&5\\-1&-1\\3&3} $$
where $e\equiv e_1,e_2$ is the standard basis of $\wR^2$ and where $g\equiv g_1,g_2,g_3$ is the standard basis of $\wR^3$. Note that
MTe=np.array([[5,5],[-1,-1],[3,3]])
MTe
array([[ 5, 5],
[-1, -1],
[ 3, 3]])
MTaTe=compute_MTaTe(MTe)
MTaTe
array([[35, 35],
[35, 35]])
eigvals,v1,v2=real_eigns_2x2(MTaTe)
eigvals
(70.0, 0.0)
v1
array([ 1., 1.])
v2
array([ 1., -1.])
Next we normalize this eigenbasis:
$$\align{ &f_1\equiv\frac{(1,1)}{\dnorm{(1,1)}} = \frac{(1,1)}{\sqrt{1+1}} = \frac1{\sqrt{2}}(1,1) \\\\ &f_2\equiv\frac{(1,-1)}{\dnorm{(1,-1)}} = \frac{(1,-1)}{\sqrt{1+1}} = \frac1{\sqrt{2}}(1,-1) }$$
or
v = [v1,v2]
f1,f2=normalize(v)
f1
array([ 0.70710678, 0.70710678])
f2
array([ 0.70710678, -0.70710678])
Note that PLRDC.1(A) implies that $f_1$ is an orthonormal basis of $\rangspb{\sqrttat}$ because the eigenvalue corresponding to $f_1$ is positive. And PLRDC.1(B) implies that $f_2$ is an orthonormal basis of $\rangspb{\sqrttat}^\perp$ because the eigenvalue corresponding to $f_2$ is zero.
Now define $S_1\in\linmapb{\rangspb{\sqrttat}}{\rangsp{T}}$ by
$$\align{ S_1f_1 &\equiv \frac1{\sqrt{\lambda_1}}Tf_1 \\ &= \frac1{\sqrt{70}}T\Prn{\frac1{\sqrt2}(1,1)} \\ &= \frac1{\sqrt{70}}\frac1{\sqrt2}T(1,1) \\ &= \frac1{\sqrt{140}}\prn{5\cdot1+5\cdot1,(-1)\cdot1+(-1)\cdot1,3\cdot1+3\cdot1} \\ &= \frac1{\sqrt{140}}\prn{5+5,(-1)+(-1),3+3} \\ &= \frac1{\sqrt{140}}(10,-2,6) }$$
or in matrix notation:
$$\align{ \mtrxof{S_1f_1,g} &\equiv \mtrxofB{\frac1{\sqrt{\lambda_1}}Tf_1,g} \\ &= \frac1{\sqrt{\lambda_1}}\mtrxof{Tf_1,g} \\ &= \frac1{\sqrt{\lambda_1}}\mtrxof{T,e,g}\mtrxof{f_1,e} \\ &= \frac1{\sqrt{70}}\pmtrx{5&5\\-1&-1\\3&3}\pmtrx{\frac1{\sqrt2}\\\frac1{\sqrt2}} \\ &= \frac1{\sqrt{70}}\frac1{\sqrt2}\pmtrx{5&5\\-1&-1\\3&3}\pmtrx{1\\1} \\ &= \frac1{\sqrt{140}}\pmtrx{5\cdot1+5\cdot1\\(-1)\cdot1+(-1)\cdot1\\3\cdot1+3\cdot1} \\ &= \frac1{\sqrt{140}}\pmtrx{5+5\\(-1)+(-1)\\3+3} \\ &= \frac1{\sqrt{140}}\pmtrx{10\\-2\\6} }$$
And define $S_2\in\linmapb{\rangspb{\sqrttat}^\perp}{\rangsp{T}^\perp}$ by
$$ S_2f_2\equiv\frac1{\sqrt{104}}(2,10,0) $$
Then
$$\align{ \mtrxof{S,f,g} &= \pmtrx{\mtrxof{S,f,g}_{:,1}&\mtrxof{S,f,g}_{:,2}} \\ &= \pmtrx{\mtrxof{Sf_1,g}&\mtrxof{Sf_2,g}} \\ &= \pmtrx{\frac{10}{\sqrt{140}}&\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}&\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&0} }$$
and
$$\align{ \mtrxof{S,f,g}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} &= \pmtrx{\frac{10}{\sqrt{140}}&\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}&\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&0}\pmtrx{\sqrt{70}&0\\0&0}\adjt{\pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}}} \\\\ &= \pmtrx{\frac{10\sqrt{70}}{\sqrt{140}}&0\\-\frac{2\sqrt{70}}{\sqrt{140}}&0\\\frac{6\sqrt{70}}{\sqrt{140}}&0}\pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}} \\\\ &= \pmtrx{\frac{10}{\sqrt{2}}&0\\-\frac{2}{\sqrt{2}}&0\\\frac{6}{\sqrt{2}}&0}\pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}} \\\\ &= \pmtrx{\frac{10}{2}&\frac{10}{2}\\-\frac22&-\frac22\\\frac{6}{2}&\frac{6}{2}} \\\\ &= \pmtrx{5&5\\-1&-1\\3&3} \\\\ &= \mtrxof{T,e,g} }$$
$\wes$
Now let’s return to Polar Decomposition. From PLRDC.3.1, for any linear map $T\in\linmap{V}{W}$ with $\dim{W}\geq\dim{V}$, we have $Tv=S\sqrttat v$ for all $v\in V$. Hence, if $e$ and $g$ are orthonormal bases of $V$ and $W$ respectively, then we compute
$$ \mtrxof{T,e,g}=\mtrxofb{S\sqrttat,e,g}=\mtrxof{S,e,g}\mtrxofb{\sqrttat,e,e} $$
Note that $\mtrxof{S,e,g}$ has orthonormal columns (by the same argument as that of SVD.1(C)). And App.28 shows that $\mtrxofb{\sqrttat,e}$ is positive semi-definite. Hence, if we can compute each of these matrices, then we have a Polar Decomposition of $T$. PLRDC.3.2 gives a formula for $S$ in terms of an orthonormal basis of $V$ that diagonalizes $\tat$. But the basis $e$ of $V$ may not diagonalize $T$. Fortunately, this is easy to work around:
Proposition PLRDC.4 - Polar Decomposition Let $T\in\linmap{V}{W}$ and let $e$ and $g$ be orthonormal bases of $V$ and $W$ respectively.
If $\dim{W}\geq\dim{V}$, then the matrix form of the Polar Decomposition of $T$ for the given bases is
$$ \mtrxof{T,e,g}=\mtrxof{S,e,g}\mtrxofb{\sqrttat,e} \tag{PLRDC.4.1} $$
The matrices on the right can be computed from an orthonormal basis $f$ of $V$ consisting of eigenvectors of $\tat$:
$$ \mtrxof{S,e,g}=\mtrxof{S,f,g}\adjt{\mtrxof{I,f,e}} \tag{PLRDC.4.2} $$
and
$$ \mtrxofb{\sqrttat,e}=\mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \tag{PLRDC.4.3} $$
Proof PLRDC.4.1 follows from PLRDC.3.1 and matrix multiplication (App.11). We also have
$$\align{ \mtrxof{S,e,g} &= \mtrxof{S,f,g}\mtrxof{I,e,f}\tag{by App.11} \\ &= \mtrxof{S,f,g}\adjt{\mtrxof{\adjt{I},f,e}}\tag{by App.4 & 7.6(c)} \\ &= \mtrxof{S,f,g}\adjt{\mtrxof{I,f,e}}\tag{by 7.6(d)} }$$
and
$$\align{ \mtrxofb{\sqrttat,e} &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\mtrxof{I,e,f}\tag{by App.6} \\ &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \\ }$$
$\wes$
Example PLRDC.5 Let’s compute the Polar Decomposition of the matrix $\mtrxof{T,e,g}$ from example SVD.3:
$$\align{ \mtrxof{S,e,g} &= \mtrxof{S,f,g}\adjt{\mtrxof{I,f,e}} \\\\ &= \pmtrx{\frac{10}{\sqrt{140}}&\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}&\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&0} \adjt{\pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}}} \\\\ &= \pmtrx{\frac{10}{\sqrt{140}}&\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}&\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&0} \pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}} \\\\ &= \frac1{\sqrt2} \pmtrx{\frac{10}{\sqrt{140}}&\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}&\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&0} \pmtrx{1&1\\1&-1} \\\\ &= \frac1{\sqrt2} \pmtrx{\frac{10}{\sqrt{140}}+\frac{2}{\sqrt{104}}&\frac{10}{\sqrt{140}}-\frac{2}{\sqrt{104}}\\-\frac{2}{\sqrt{140}}+\frac{10}{\sqrt{104}}&-\frac{2}{\sqrt{140}}-\frac{10}{\sqrt{104}}\\\frac{6}{\sqrt{140}}&\frac{6}{\sqrt{140}}} }$$
We can check that $\mtrxof{S,e,g}$ has orthonormal columns:
MSeg=(1/np.sqrt(2))*np.array([[10/np.sqrt(140)+2/np.sqrt(104),10/np.sqrt(140)-2/np.sqrt(104)],
[-2/np.sqrt(140)+10/np.sqrt(104),-2/np.sqrt(140)-10/np.sqrt(104)],
[6/np.sqrt(140),6/np.sqrt(140)]])
MSeg
array([[ 0.73628935, 0.45893926],
[ 0.57385238, -0.81289811],
[ 0.35856858, 0.35856858]])
Rn_innprd(MSeg[:,0],MSeg[:,1])
-1.6653345369377348e-16
Rn_innprd(MSeg[:,0],MSeg[:,0])
0.99999999999999978
Rn_innprd(MSeg[:,1],MSeg[:,1])
1.0
And we can spot check that $\mtrxof{S,e,g}$ preserves norms:
def check_isometry(S,x,tol=1e-12,prnt=True):
Sx=S.dot(x)
Sxn=Rn_norm(Sx)
xn=Rn_norm(x)
d=np.abs(Sxn-xn)
if prnt:
print("Sxn={} xn={} diff={} iso={}".format(Sxn,xn,d,d<=tol))
return d
x=np.array([1,1])
check_isometry(MSeg,x)
Sxn=1.414213562373095 xn=1.4142135623730951 diff=2.220446049250313e-16 iso=True
2.2204460492503131e-16
x=np.array([-9,13])
check_isometry(MSeg,x)
Sxn=15.811388300841896 xn=15.811388300841896 diff=0.0 iso=True
0.0
x=np.array([141,-71341])
check_isometry(MSeg,x)
Sxn=71341.1393376921 xn=71341.1393376921 diff=0.0 iso=True
0.0
Now let’s look at $\mtrxofb{\sqrttat,e}$:
$$\align{ \mtrxofb{\sqrttat,e} &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \\\\ &= \pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}} \pmtrx{\sqrt{70}&0\\0&0} \adjt{\pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}}} \\\\ &= \pmtrx{\frac{\sqrt{70}}{\sqrt2}&0\\\frac{\sqrt{70}}{\sqrt2}&0} \pmtrx{\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}} \\\\ &= \frac{\sqrt{70}}{\sqrt2}\frac{1}{\sqrt{2}}\pmtrx{1&0\\1&0}\pmtrx{1&1\\1&-1} \\\\ &= \frac{\sqrt{70}}{2}\pmtrx{1&1\\1&1} }$$
Let’s verify that $\mtrxofb{\sqrttat,e}$ is positive semi-definite. Clearly it’s symmetric. We also have
$$\align{ \pmtrx{x\\y}^t\mtrxofb{\sqrttat,e}\pmtrx{x\\y} &= \pmtrx{x\\y}^t\frac{\sqrt{70}}{2}\pmtrx{1&1\\1&1}\pmtrx{x\\y} \\\\ &= \frac{\sqrt{70}}{2}\pmtrx{x&y}\pmtrx{x+y\\x+y} \\\\ &= \frac{\sqrt{70}}{2}(x^2+xy+xy+y^2) \\\\ &= \frac{\sqrt{70}}{2}(x+y)^2 \\\\ &\geq 0 }$$
And we can verify that $\mtrxof{T,e,g}=\mtrxof{S,e,g}\mtrxofb{\sqrttat,e}$:
MSqrtTTe=np.sqrt(70)/2*np.array([[1,1],[1,1]])
MSeg.dot(MSqrtTTe)
array([[ 5., 5.],
[-1., -1.],
[ 3., 3.]])
$\wes$
Example PLRDC.6 Let’s compute the Polar Decomposition of the matrix $\mtrxof{T,e}$ from example SVD.2:
$$\align{ \mtrxof{S,e,e} &= \mtrxof{S,f,e}\adjt{\mtrxof{I,f,e}} \\\\ &= \pmtrx{\frac1{\sqrt2}&\frac1{\sqrt2}\\\frac1{\sqrt2}&-\frac1{\sqrt2}} \adjt{\pmtrx{\frac{1}{\sqrt{10}}&\frac{3}{\sqrt{10}}\\\frac{3}{\sqrt{10}}&-\frac{1}{\sqrt{10}}}} \\\\ }$$
MSfe=(1/np.sqrt(2))*np.array([[1,1],[1,-1]])
MSfe
array([[ 0.70710678, 0.70710678],
[ 0.70710678, -0.70710678]])
MIfe=np.array([[1/np.sqrt(10),3/np.sqrt(10)],[3/np.sqrt(10),-1/np.sqrt(10)]])
MIfe
array([[ 0.31622777, 0.9486833 ],
[ 0.9486833 , -0.31622777]])
MSee=MSfe.dot(MIfe.T)
MSee
array([[ 0.89442719, 0.4472136 ],
[-0.4472136 , 0.89442719]])
$$\align{ \mtrxofb{\sqrttat,e} &= \mtrxof{I,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}} \\\\ &= \pmtrx{\frac{1}{\sqrt{10}}&\frac{3}{\sqrt{10}}\\\frac{3}{\sqrt{10}}&-\frac{1}{\sqrt{10}}} \pmtrx{\sqrt{80}&0\\0&\sqrt{20}} \adjt{\pmtrx{\frac{1}{\sqrt{10}}&\frac{3}{\sqrt{10}}\\\frac{3}{\sqrt{10}}&-\frac{1}{\sqrt{10}}}} \\\\ }$$
D=np.array([[np.sqrt(80),0],[0,np.sqrt(20)]])
D
array([[ 8.94427191, 0. ],
[ 0. , 4.47213595]])
MSqrtTaTe=MIfe.dot(D).dot(MIfe.T)
MSqrtTaTe
array([[ 4.91934955, 1.34164079],
[ 1.34164079, 8.49705831]])
MSee.dot(MSqrtTaTe)
array([[ 5., 5.],
[-1., 7.]])
Note that the matrix $\mtrxofb{\sqrttat,e}$ is a dilation. We can see this by plotting $\mtrxofb{\sqrttat,e}\mtrxof{x,e}$ for $x$ with $\dnorm{x}=1$. That is, all $x$ in the unit circle in $\wR^2$:
x_data,y_data=[],[]
for t in np.linspace(0,2*np.pi,100):
x_data.append(np.cos(t))
y_data.append(np.sin(t))
def make_data(M):
xd,yd=[],[]
for t in np.linspace(0,2*np.pi,100):
x=np.array([np.cos(t),np.sin(t)])
Mx=M.dot(x)
xd.append(Mx[0])
yd.append(Mx[1])
return xd,yd
xd,yd=make_data(MSqrtTaTe)
plt.plot(x_data,y_data,color='blue', linestyle='-', linewidth=2)
[<matplotlib.lines.Line2D at 0x116d3de10>]
plt.plot(xd,yd,color='red', linestyle='-', linewidth=2)
[<matplotlib.lines.Line2D at 0x116d486a0>]
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
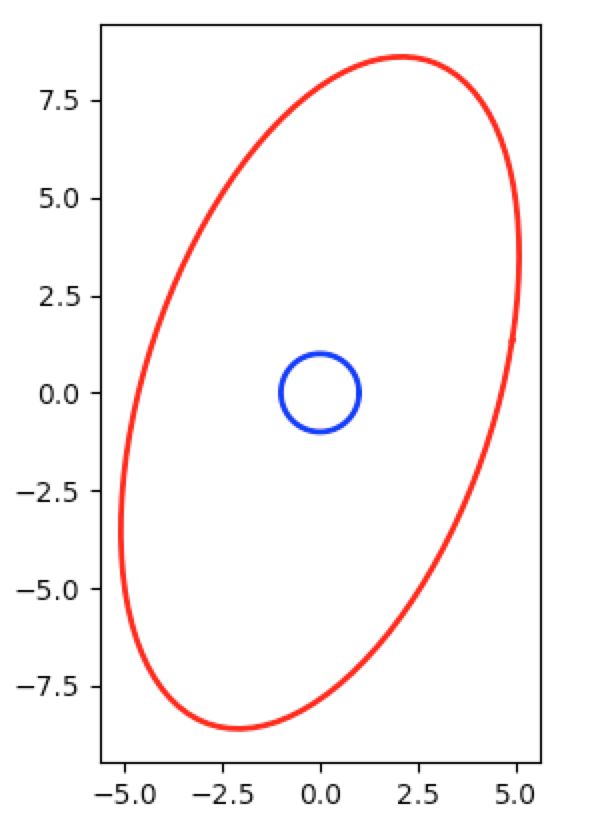
Whereas $\mtrxof{S,e,e}$ is a rotation:
xd,yd=make_data(MSee)
plt.plot(x_data,y_data,color='blue', linestyle='-', linewidth=2)
[<matplotlib.lines.Line2D at 0x124895278>]
plt.plot(xd,yd,color='red', linestyle='-', linewidth=2)
[<matplotlib.lines.Line2D at 0x12489c320>]
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
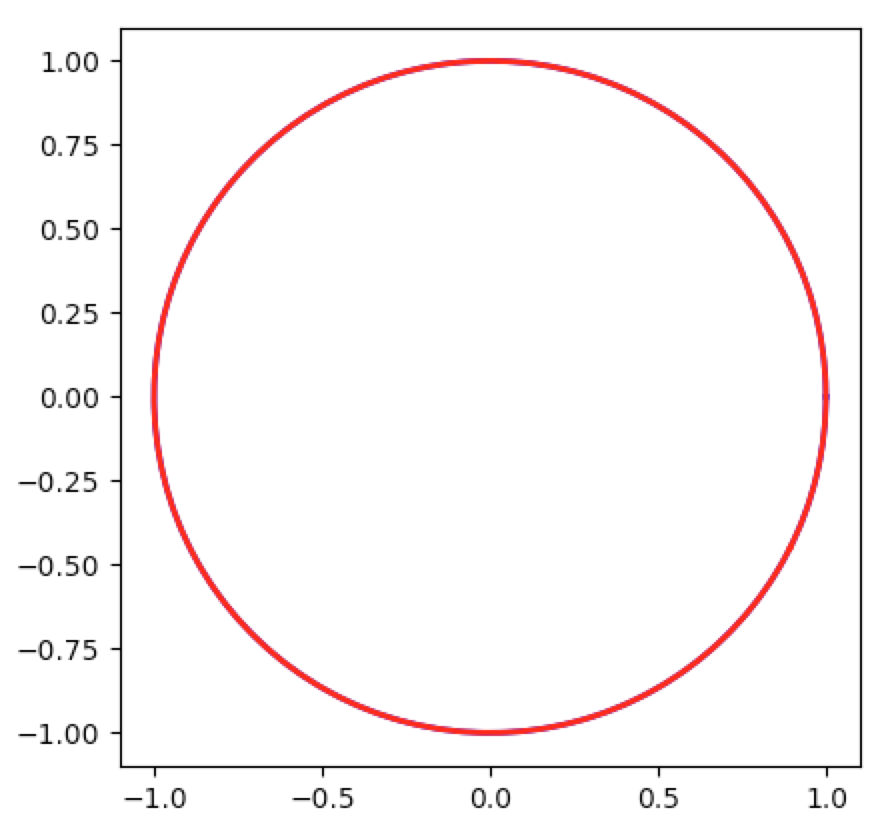
Corollary SVD.4 Suppose $T\wiov$ is self-adjoint and invertible. Then any Singular Value Decomposition (SVD.1.1) of $T$ is also a Spectral Decomposition (SPECT.1.1) of $T$.
That is, if $e\equiv e_1,\dots,e_n$ is any orthonormal basis of $V$ and $f\equiv f_1,\dots,f_n$ is an orthonormal basis of $V$ consisting of eigenvectors of $\tat$, then the isometry $S$ in SVD.1.1 is the identity map, $\sqrttat=T$, and
$$ \mtrxof{T,e}=\mtrxof{S,f,e}\mtrxofb{\sqrttat,f}\adjt{\mtrxof{I,f,e}}=\mtrxof{I,f,e}\mtrxof{T,f}\adjt{\mtrxof{I,f,e}} $$
is both a Singular Value Decomposition (SVD.1.1) and a Spectral Decomposition (SPECT.1.1) of $T$.
Proof Let $\lambda_1,\dots,\lambda_n$ be the eigenvalues corresponding to the eigenbasis $f_1,\dots,f_n$. Recall from the proof of SVD.1(A) and from PLRDC.3.2, that the isometry $S$ satisfies
$$ Sf_j=\cases{\frac1{\sqrt{\lambda_j}}Tf_j&\text{for }j=1,\dots,\dim{\rangsp{T}}\\h_j&\text{for }j=\dim{\rangsp{T}}+1,\dots,n} $$
where $h_{\dim{\rangsp{T}}+1},\dots,h_n$ is any orthonormal list in $\rangsp{T}^\perp$ of length $n-\dim{\rangsp{T}}$. Since $T$ is invertible, then it’s surjective (by 3.69). Hence $\rangsp{T}=V$ and $\dim{\rangsp{T}}=\dim{V}=n$. Hence
$$ Sf_j=\frac1{\sqrt{\lambda_j}}Tf_j\quad\text{for }j=1,\dots,n $$
Note that $T^2=TT=\tat$ and that the operator $\sqrttat$ is unique (by 7.36). Hence $T=\sqrttat$. Also note that App.2 gives that $f_j$ is an eigenvector of $\sqrttat$ corresponding to eigenvalue $\sqrt{\lambda_j}$. Then
$$ Sf_j=\frac1{\sqrt{\lambda_j}}Tf_j=\frac1{\sqrt{\lambda_j}}\sqrttat f_j=\frac1{\sqrt{\lambda_j}}\sqrt{\lambda_j}f_j=f_j $$
Hence $S=I$ (by 3.5 or App.14). $\wes$
Appendix
Adjoint $\adjt{T}$
Suppose $T\in\linmap{V}{W}$. Fix $w\in W$. Define $S_w:W\mapsto\wF$ by $S_w(\cdot)\equiv\innprd{\cdot}{w}$. Then 6.7(a) shows that $S_w$ is a linear map. Since the product (i.e. composition) of linear maps is linear, then $S_wT=S_w\circ T\in\linmap{V}{\wF}$.
Define the linear functional $\varphi_{T,w}\in\linmap{V}{\wF}$ by $\varphi_{T,w}\equiv S_wT$. This linear functional depends on $T$ and $w$:
$$ \varphi_{T,w}(v)\equiv (S_wT)v=S_w(Tv)=\innprd{Tv}{w} $$
By the Riesz Representation Theorem (6.42), there exists a unique vector in $V$, call it $\adjt{T}w$, such that this linear functional is given by taking the inner product with it. That is, there exists a unique vector $\adjt{T}w\in V$ such that, for every $v\in V$, we have
$$ \innprd{Tv}{w}_W=\varphi_{T,w}(v)=\innprd{v}{\adjt{T}w}_V \tag{Adj.1} $$
Since $\varphi_{T,w}$ depends on $T$ and $w$, then $\adjt{T}$ depends on $w$. That is, $\adjt{T}$ is a function of $w$. And we can show that $\adjt{T}$ is unique. Suppose there exists another function $X:W\mapsto V$ that satisfies Adj.1 but with $Xz\neq \adjt{T}z$ for some $z\in W$. Then
$$ \innprd{v}{Xz}_V=\varphi_{T,z}(v)=\innprd{v}{\adjt{T}z}_V\quad\quad Xz\neq \adjt{T}z $$
But this contradicts the Riesz implication of the existence of the unique $\adjt{T}z\in V$ satisfying this equality.
Axler (7.5) also shows that $\adjt{T}\in\linmap{W}{V}$. Hence we have established that there exists a unique linear map $\adjt{T}$ from $W$ to $V$ satisfying
$$ \innprd{Tv}{w}_W=\innprd{v}{\adjt{T}w}_V \tag{Adj.2} $$
for every $v\in V$ and every $w\in W$.
Let $e_1,\dots,e_n$ be an orthonormal basis of $V$. Then 6.43 gives
$$ \adjt{T}w=\sum_{k=1}^n\cj{\varphi_{T,w}(e_k)}e_k=\sum_{k=1}^n\cj{\innprd{Te_k}{w}}e_k=\sum_{k=1}^n\innprd{w}{Te_k}e_k \tag{Adj.3} $$
Since $\adjt{T}w\in V$, this equality can also be derived from 6.30:
$$ \adjt{T}w=\sum_{k=1}^n\innprd{\adjt{T}w}{e_k}e_k=\sum_{k=1}^n\innprd{w}{Te_k}e_k $$
General
Proposition App.1 Let $\lambda_1,\dots,\lambda_n$ be nonnegative and let $e_1,\dots,e_n$ be an orthonormal basis of $V$. Define $R\in\oper{V}$ by $Re_j\equiv\sqrt{\lambda_j}e_j$ for $j=1,\dots,n$. Then $R$ is a positive operator.
Proof Formula Adj.3 gives
$$ R^*e_j=\sum_{k=1}^n\innprd{e_j}{Re_k}e_k=\sum_{k=1}^n\innprd{e_j}{\sqrt{\lambda_k}e_k}e_k=\sum_{k=1}^n\cj{\sqrt{\lambda_k}}\innprd{e_j}{e_k}e_k=\sum_{k=1}^n\sqrt{\lambda_k}\mathbb{1}_{j=k}e_k=\sqrt{\lambda_j}e_j=Re_j $$
Hence $R^*=R$ and $R$ is self-adjoint. Let $v\in V$. Then $v=\sum_{k=1}^n\innprd{v}{e_k}e_k$ and
$$\align{ \innprd{Rv}{v} &= \innprdBgg{R\Prn{\sum_{j=1}^n\innprd{v}{e_j}e_j}}{\sum_{k=1}^n\innprd{v}{e_k}e_k} \\ &= \innprdBgg{\sum_{j=1}^n\innprd{v}{e_j}Re_j}{\sum_{k=1}^n\innprd{v}{e_k}e_k} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprdbg{\innprd{v}{e_j}Re_j}{\innprd{v}{e_k}e_k} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprd{v}{e_j}\cj{\innprd{v}{e_k}}\innprd{Re_j}{e_k} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprd{v}{e_j}\cj{\innprd{v}{e_k}}\innprd{\sqrt{\lambda_j}e_j}{e_k} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprd{v}{e_j}\cj{\innprd{v}{e_k}}\sqrt{\lambda_j}\innprd{e_j}{e_k} \\ &= \sum_{j=1}^n\sum_{k=1}^n\innprd{v}{e_j}\cj{\innprd{v}{e_k}}\sqrt{\lambda_j}\mathbb{1}_{j=k} \\ &= \sum_{j=1}^n\innprd{v}{e_j}\cj{\innprd{v}{e_j}}\sqrt{\lambda_j} \\ &= \sum_{j=1}^n\normb{\innprd{v}{e_j}}^2\sqrt{\lambda_j} \\ &\geq0 }$$
$\wes$
Proposition App.2 Let $T\in\linmap{V}{W}$. Then $\tat\wiov$ is a positive operator.
Also, let $e_1,\dots,e_n$ denote an orthonormal basis of $V$. Then $e_1,\dots,e_n$ consists of eigenvectors of $\tat$ corresponding to the eigenvalues $\lambda_1,\dots,\lambda_n$ if and only if $e_1,\dots,e_n$ consists of eigenvectors of $\sqrttat$ corresponding to the eigenvalues $\sqrt{\lambda_1},\dots,\sqrt{\lambda_n}$. That is
$$ \tat e_j=\lambda_j e_j\qd\text{for }j=1,\dots,n \dq\iff\dq \sqrttat e_j=\sqrt{\lambda_j}e_j\qd\text{for }j=1,\dots,n $$
Proof Note that $\adjt{(\tat)}=\adjt{T}\adjt{(\adjt{T})}=\tat$. Hence $\tat$ is self-adjoint. Also note that $\innprd{\tat v}{v}=\innprd{Tv}{Tv}\geq 0$ for every $v\in V$. Hence $\tat$ is a positive operator.
Suppose $e_1,\dots,e_n$ consists of eigenvectors of $\tat$ corresponding to the eigenvalues $\lambda_1,\dots,\lambda_n$ (existence given by the Spectral Theorem). Then 7.35(b) implies that the eigenvalues $\lambda_1,\dots,\lambda_n$ of $\tat$ are all nonnegative. Now define $R\wiov$ by
$$ Re_j=\sqrt{\lambda_j}e_j\qd\text{for }j=1,\dots,n $$
Then $R$ is positive (by App.1) and, for $j=1,\dots,n$, we have
$$ R^2e_j=R\prn{\sqrt{\lambda_j}e_j}=\sqrt{\lambda_j}Re_j=\sqrt{\lambda_j}\sqrt{\lambda_j}e_j=\lambda_je_j=\tat e_j $$
Hence, by App.14, 7.36, and 7.44, we have $\sqrt{\tat}=R$.
Conversely, suppose $e_1,\dots,e_n$ consists of eigenvectors of $\sqrttat$ corresponding to the eigenvalues $\sqrt{\lambda_1},\dots,\sqrt{\lambda_n}$ (existence given by the Spectral Theorem). Then
$$ \tat e_j=\sqrttat\sqrttat e_j=\sqrttat\prn{\sqrt{\lambda_j}e_j}=\sqrt{\lambda_j}\sqrttat e_j=\sqrt{\lambda_j}\sqrt{\lambda_j}e_j=\lambda_je_j $$
for $j=1,\dots,n$. $\wes$
Proposition App.3<–>7.52 Let $n\equiv\dim{V}$ and let $T\wiov$. Then there are $n$ singular values of $T$ and they are the nonnegative square roots of the eigenvalues of $\tat$, with each eigenvalue $\lambda$ repeated $\dim{\eignsp{\lambda}{\tat}}$ times.
Proof From App.2, we see that
$$ \sqrt{\tat}e_j=\sqrt{\lambda_j}e_j\qd\text{for }j=1,\dots,n $$
where $e_1,\dots,e_n$ is an orthonormal eigenbasis of $V$ corresponding to the nonnegative eigenvalues $\lambda_1,\dots,\lambda_n$ of $\tat$. Hence $\sqrt{\tat}$ has $n$ nonnegative eigenvalues (counting multiples) and
$$ n=\sum_{k=1}^n\dim{\eignspb{\lambda_k}{\sqrt{\tat}}} $$
By definition (7.49), the singular values of $T$ are the eigenvalues of $\sqrt{\tat}$, with each eigenvalue $\lambda$ repeated $\dim{\eignsp{\lambda}{\sqrt{\tat}}}$ times. $\wes$
Proposition App.4<–>7.10 Conjugate Transpose Let $T\in\linmap{V}{W}$, let $e\equiv e_1,\dots,e_n$ be an orthonormal basis of $V$, and let $f\equiv f_1,\dots,f_m$ be an orthonormal basis of $W$. Then
$$ \adjt{\mtrxof{T,e,f}}=\mtrxof{\adjtT,f,e} $$
Proof Note that 6.30 gives
$$ Te_k=\sum_{j=1}^m\innprd{Te_k}{f_j}_Wf_j $$
$$ \adjt{T}f_k=\sum_{j=1}^n\innprd{\adjt{T}f_k}{e_j}_Ve_j $$
Hence
$$\align{ \adjt{\mtrxof{T,e,f}} &= \adjt{\pmtrx{\mtrxof{T,e,f}_{:,1}&\dotsb&\mtrxof{T,e,f}_{:,n}}} \\\\ &= \adjt{\pmtrx{\mtrxof{Te_1,f}&\dotsb&\mtrxof{Te_n,f}}} \\\\ &= \adjt{\pmtrx{\innprd{Te_1}{f_1}_W&\dotsb&\innprd{Te_n}{f_1}_W\\\vdots&\ddots&\vdots\\\innprd{Te_1}{f_m}_W&\dotsb&\innprd{Te_n}{f_m}_W}} \\\\ &= \pmtrx{\cj{\innprd{Te_1}{f_1}_W}&\dotsb&\cj{\innprd{Te_1}{f_m}_W}\\\vdots&\ddots&\vdots\\\cj{\innprd{Te_n}{f_1}_W}&\dotsb&\cj{\innprd{Te_n}{f_m}_W}} \\\\ &= \pmtrx{\innprd{f_1}{Te_1}_W&\dotsb&\innprd{f_m}{Te_1}_W\\\vdots&\ddots&\vdots\\\innprd{f_1}{Te_n}_W&\dotsb&\innprd{f_m}{Te_n}_W} \\\\ &= \pmtrx{\innprd{\adjt{T}f_1}{e_1}_V&\dotsb&\innprd{\adjt{T}f_m}{e_1}_V\\\vdots&\ddots&\vdots\\\innprd{\adjt{T}f_1}{e_n}_V&\dotsb&\innprd{\adjt{T}f_m}{e_n}_V} \\\\ &= \pmtrx{\mtrxof{\adjt{T}f_1,e}&\dotsb&\mtrxof{\adjt{T}f_m,e}} \\\\ &= \pmtrx{\mtrxof{\adjt{T},f,e}_{:,1}&\dotsb&\mtrxof{\adjt{T},f,e}_{:,m}} \\\\ &= \mtrxof{\adjtT,f,e} }$$
$\wes$
Proposition App.5<–>7.42 Let $S\in\linmap{V}{W}$ with $\dim{V}=\dim{W}$. Then the following are equivalent:
(a) $S$ is an isometry
(b) $\innprd{Su}{Sv}_W=\innprd{u}{v}_V$ for all $u,v\in V$
(c) $Se_1,\dots,Se_m$ is orthonormal for every orthonormal list $e_1,\dots,e_m$ in $V$
(d) there exists an orthonormal basis $e_1,\dots,e_n$ of $V$ such that $Se_1,\dots,Se_n$ is orthonormal
(e) $\adjt{S}S=I_V$
(f) $S\adjt{S}=I_W$
(g) $\adjt{S}$ is an isometry
(h) $S$ is invertible and $\inv{S}=\adjt{S}$
Proof (a)$\implies$(b) Let $u,v\in V$. If $V$ is a real inner product space, then
$$\align{ \innprd{Su}{Sv}_W &= \frac{\dnorm{Su+Sv}_W^2-\dnorm{Su-Sv}_W^2}4\tag{by App.15} \\ &= \frac{\dnorm{S(u+v)}_W^2-\dnorm{S(u-v)}_W^2}4 \\ &= \frac{\dnorm{u+v}_V^2-\dnorm{u-v}_V^2}4\tag{because $S$ isometric} \\ &= \innprd{u}{v}_V\tag{by App.15} }$$
If $V$ is a complex inner product space, then
$$\align{ \innprd{Su}{Sv}_W &= \frac{\dnorm{Su+Sv}_W^2-\dnorm{Su-Sv}_W^2}4 \\ &+ \frac{\dnorm{Su+iSv}_W^2i-\dnorm{Su-iSv}_W^2i}4\tag{by App.16} \\ &= \frac{\dnorm{S(u+v)}_W^2-\dnorm{S(u-v)}_W^2}4 \\ &+ \frac{\dnorm{S(u+iv)}_W^2i-\dnorm{S(u-iv)}_W^2i}4 \\ &= \frac{\dnorm{u+v}_V^2-\dnorm{u-v}_V^2+\dnorm{u+iv}_V^2i-\dnorm{u-iv}_V^2i}4\tag{because $S$ isometric} \\ &= \innprd{u}{v}_V\tag{by App.16} }$$
Proof (b)$\implies$(c) Let $e_1,\dots,e_m$ be an orthonormal list in $V$. Then
$$ \innprd{Se_j}{Se_k}=\innprd{e_j}{e_k}=\cases{1&j=k\\0&j\neq k} $$
Proof (c)$\implies$(d) This is clear.
Proof (d)$\implies$(e) Let $e_1,\dots,e_n$ denote an orthonormal basis of $V$. Then, for any $j,k=1,\dots,n$, we have
$$ \innprd{\adjt{S}Se_j}{e_k}=\innprd{Se_j}{Se_k}=\innprd{e_j}{e_k} $$
and App.21 implies that $\adjt{S}S=I_V$.
Proof (e)$\implies$(f) This follows from App.19.
Proof (f)$\implies$(g) For any $w\in W$, we have
$$ \dnorm{\adjt{S}w}_V^2=\innprd{\adjt{S}w}{\adjt{S}w}_V=\innprd{S\adjt{S}w}{w}_W=\innprd{I_Ww}{w}_W=\innprd{w}{w}_W=\dnorm{w}_W^2 $$
Proof (g)$\implies$(h) We know that (a)$\implies$(e). Hence, since $\adjt{S}$ is an isometry, then
$$ I_W=\adjt{(\adjt{S})}\adjt{S}=S\adjt{S} $$
And we know that (a)$\implies$(f). Hence, since $\adjt{S}$ is an isometry, then
$$ I_V=\adjt{S}\adjt{(\adjt{S})}=\adjt{S}S $$
Hence, by definition 3.53, $S$ is invertible and $\inv{S}=\adjt{S}$.
Proof (h)$\implies$(a) Since $S$ is invertible and $\inv{S}=\adjt{S}$, then $\adjt{S}S=I_V$. Hence, for any $v\in V$, we have
$$ \dnorm{Sv}_W^2=\innprd{Sv}{Sv}_W=\innprd{\adjt{S}Sv}{v}_V=\innprd{I_Vv}{v}_V=\innprd{v}{v}_V=\dnorm{v}_V^2 $$
$\wes$
Proposition App.6 <–> 10.7 Change of Basis Suppose $T\wiov$. Let $u\equiv u_1,\dots,u_n$ and $v\equiv v_1,\dots,v_n$ be bases of $V$. Then
$$\align{ \mtrxof{T,u} &= \mtrxof{I,v,u}\mtrxof{T,v}\mtrxof{I,u,v} \\ &= \inv{\mtrxof{I,u,v}}\mtrxof{T,v}\mtrxof{I,u,v} }$$
Proof
$$\align{ \inv{\mtrxof{I,u,v}}\mtrxof{T,v}\mtrxof{I,u,v} &= \mtrxof{I,v,u}\mtrxof{T,v,v}\mtrxof{I,u,v}\tag{by App.12} \\ &= \mtrxof{IT,v,u}\mtrxof{I,u,v}\tag{by App.11} \\ &= \mtrxof{T,v,u}\mtrxof{I,u,v} \\ &= \mtrxof{TI,u,u}\tag{by App.11} \\ &= \mtrxof{T,u} }$$
$\wes$
Proposition App.7 Let $T\in\linmap{V}{W}$. Then $\dnorm{Tv}_W=\dnorm{\sqrttat v}_V$ for all $v\in V$.
Proof For any $v\in V$, we have
$$\align{ \dnorm{Tv}_W^2 &= \innprd{Tv}{Tv}_W \\ &= \innprd{\tat v}{v}_V \\ &= \innprdbg{\sqrttat\sqrttat v}{v}_V \\ &= \innprdbg{\sqrttat v}{\adjt{\prn{\sqrttat}} v}_V \\ &= \innprdbg{\sqrttat v}{\sqrttat v}_V \\ &= \dnorm{\sqrttat v}_V^2 }$$
The next-to-last equality holds because $\sqrttat$ is positive and hence self-adjoint. $\wes$
Proposition App.8 Let $T\in\linmap{V}{W}$. Then
$$ \nullsp{T}=\nullspb{\sqrttat}=\rangspb{\sqrttat}^\perp $$
Proof Let $u\in\nullsp{T}$. Then 6.10(a) gives the first equality and App.7 gives the second equality:
$$ 0=\dnorm{Tu}_W=\dnorm{\sqrttat u}_V $$
Hence, by 6.10(a), $\sqrttat u=0$. Hence $u\in\nullspb{\sqrttat}$ and $\nullsp{T}\subset\nullspb{\sqrttat}$.
Conversely, let $u\in\nullspb{\sqrttat}$. Then
$$ 0=\dnorm{\sqrttat u}_V=\dnorm{Tu}_W $$
Hence $Tu=0$ and $u\in\nullsp{T}$ and $\nullspb{\sqrttat}\subset\nullsp{T}$. Hence $\nullspb{\sqrttat}=\nullsp{T}$. Also note that
$$ \nullspb{\sqrttat}=\nullspb{\adjt{\prn{\sqrttat}}}=\rangspb{\sqrttat}^\perp $$
The first equality holds because $\sqrttat$ is positive and hence self-adjoint. The second equality follows from 7.7(a). $\wes$
Proposition App.9<–>Exercise 5.C.7 Suppose $T\in\lnmpsb(V)$ has a diagonal matrix $A$ with respect to some basis of $V$. And let $\lambda\in\mathbb{F}$. Then $\lambda$ appears on the diagonal of $A$ precisely $\dim{\eignsb(\lambda,T)}$ times.
Proof Let $v_1,\dots,v_n$ be the basis with respect to which $T$ has the diagonal matrix $A$. And let $\beta_1,\dots,\beta_n$ be the nondistinct eigenvalues corresponding $v_1,\dots,v_n$. Then, by 5.32, the $\beta$’s are precisely the entries on the diagonal of $\mtrxofb{T,(v_1,\dots,v_n)}$:
$$ \nbmtrx{ Tv_1=\beta_1v_1\\ Tv_2=\beta_2v_2\\ \vdots\\ Tv_n=\beta_nv_n } \dq\dq \iff \dq\dq \mtrxofb{T,(v_1,\dots,v_n)}=\pmtrx{\beta_1&&&&\\&\beta_2&&&\\&&\ddots&&\\&&&\ddots&\\&&&&\beta_n} $$
Let $\lambda_1,\dots,\lambda_m$ be the distinct eigenvalues of $T$. For $k=1,\dots,m$, define $\phi_k$ to be the list of indices of nondistinct eigenvalues $\beta_1,\dots,\beta_n$ that are equal to $\lambda_k$:
$$ \phi_k\equiv\prn{j\in\set{1,\dots,n}:\lambda_k=\beta_j} $$
For intuition, here’s a concrete example: suppose $n=6$ and suppose that there are $4$ distinct eigenvalues. Then
$$ \mtrxofb{T,(v_1,\dots,v_6)}=\pmtrx{\lambda_1&&&&&\\&\lambda_2&&&&\\&&\lambda_3&&&\\&&&\lambda_2&&\\&&&&\lambda_4&\\&&&&&\lambda_3}=\pmtrx{\beta_1&&&&&\\&\beta_2&&&&\\&&\beta_3&&&\\&&&\beta_4&&\\&&&&\beta_5&\\&&&&&\beta_6} $$
and
$$ \phi_1=(1) \dq \phi_2=(2,4) \dq \phi_3=(3,6) \dq \phi_4=(5) $$
Note that $\text{len}(\phi_k)$ equals the number of times that $\lambda_k$ appears on the diagonal. So it suffices to show that $\text{len}(\phi_k)=\dim{\eignsb(\lambda_k,T)}$.
First we will show that $\eignsb(\lambda_k,T)=\bigoplus_{j\in\phi_k}\text{span}(v_j)$. Let $w\in\eignsb(\lambda_k,T)\subset V$. Then $w=\sum_{j=1}^na_jv_j$ for some $a_1,\dots,a_n\in\wF$ and
$$\begin{align*} 0 &= (T-\lambda_kI)w \\ &= (T-\lambda_kI)\Big(\sum_{j=1}^na_jv_j\Big) \\ &= \sum_{j=1}^na_j(T-\lambda_kI)v_j \\ &= \sum_{j=1}^na_j(Tv_j-\lambda_kIv_j) \\ &= \sum_{j=1}^na_j(\beta_jv_j-\lambda_kv_j) \\ &= \sum_{j=1}^na_j(\beta_j-\lambda_k)v_j \\ &= \sum_{j\notin\phi_k}a_j(\beta_j-\lambda_k)v_j\tag{since $\beta_j=\lambda_k$ for $j\in\phi_k$} \end{align*}$$
Since $0\neq\beta_j-\lambda_k$ for $j\notin\phi_k$ and the $v_j$ are linearly independent, then $0=a_j$ for $j\notin\phi_k$ and
$$ w=\sum_{j=1}^na_jv_j=\sum_{j\in\phi_k}a_jv_j\in\sum_{j\in\phi_k}\span{v_j} $$
since $a_jv_j\in\text{span}(v_j)$. Hence
$$ \eignsb(\lambda_k,T)\subset\sum_{j\in\phi_k}\text{span}(v_j) $$
In the other direction, let $w\in\sum_{j\in\phi_k}\text{span}(v_j)$. Then $w=\sum_{j\in\phi_k}s_j$ where $s_j\in\text{span}(v_j)$ for $j\in\phi_k$. Hence $s_j=a_jv_j$ and $w=\sum_{j\in\phi_k}a_jv_j$ and
$$ Tw = T\Big(\sum_{j\in\phi_k}a_jv_j\Big) = \sum_{j\in\phi_k}a_jTv_j = \sum_{j\in\phi_k}a_j\lambda_kv_j = \lambda_k\sum_{j\in\phi_k}a_jv_j = \lambda_kw $$
Hence $w$ is an eigenvector of $T$ corresponding to $\lambda_k$ and $w\in\eignsb(\lambda_k,T)$. Hence $\sum_{j\in\phi_k}\text{span}(v_j)\subset\eignsb(\lambda_k,T)$ and
$$ \sum_{j\in\phi_k}\text{span}(v_j)=\eignsb(\lambda_k,T) $$
Next we want to show that $\sum_{j\in\phi_k}\text{span}(v_j)$ is a direct sum (this is unnecessary to reach the desired conclusion but it’s good to see). Suppose $s_j\in\span{v_j}$ for $j\in\phi_k$. Then $s_j=a_jv_j$ for some $a_j\in\wF$. Further suppose that $0=\sum_{j\in\phi_k}s_j$. Then
$$ 0 = \sum_{j\in\phi_k}s_j = \sum_{j\in\phi_k}a_jv_j $$
Then the linear independence of $(v_j)_{j\in\phi_k}$ implies that $0=a_j$ for $j\in\phi_k$. Hence $0=s_j$ for $j\in\phi_k$ and $\bigoplus_{j\in\phi_k}\text{span}(v_j)$ is a direct sum (by 1.44, p.23).
Proposition App.10 implies that $(v_j)_{j\in\phi_k}$ is a basis of $\bigoplus_{j\in\phi_k}\text{span}(v_j)$. Hence
$$ \dim{\bigoplus_{j\in\phi_k}\text{span}(v_j)}=\text{len}\big((v_j)_{j\in\phi_k}\big)=\text{len}(\phi_k) $$
and
$$ \dim{\eignsb(\lambda_k,T)}=\dim{\sum_{j\in\phi_k}\text{span}(v_j)}=\dim{\bigoplus_{j\in\phi_k}\text{span}(v_j)}=\text{len}(\phi_k) $$
$\wes$
Proposition App.10 Let $U_1,…,U_m$ be finite subspaces of $V$. Let $u_1^{(i)},…,u_{n_i}^{(i)}$ be a basis for $U_i$ for $i=1,…,m$ and define the list $W\equiv u_1^{(1)},…,u_{n_1}^{(1)},u_1^{(2)},…,u_{n_2}^{(2)},…,u_1^{(m)},…,u_{n_m}^{(m)}$. That is, $W$ is the list of all of the vectors in all of the given bases for $U_1,…,U_m$. Then
$$ U_1+\dots+U_m=\text{span}(W) $$
and these conditions are equivalent:
$\quad(1)\quad \dim{(U_1+\dots+U_m)}=\text{len}(W)$
$\quad(2)\quad W$ is linearly independent in $U_1+\dots+U_m$
$\quad(3)\quad U_1+\dots+U_m=U_1\oplus\dots\oplus U_m$ is a direct sum
where $\text{len}(W)$ denotes the number of vectors in the list $W$.
Proof Let $u\in U_1+\dots+U_m$. Then $u=u_1+\dots+u_m$ for some $u_1\in U_1,…,u_m\in U_m$. And
$$ u_i=a_1^{(i)}u_1^{(i)}+\dots+a_{n_i}^{(i)}u_{n_i}^{(i)}=\sum_{j=1}^{n_i}a_j^{(i)}u_{j}^{(i)} $$
for some $a_j^{(i)}\in\mathbb{F}$ since $u_i\in U_i=\text{span}(u_1^{(i)},…,u_{n_i}^{(i)})$. Hence
$$ u=\sum_{i=1}^{m}u_i=\sum_{i=1}^{m}\big(a_1^{(i)}u_1^{(i)}+\dots+a_{n_i}^{(i)}u_{n_i}^{(i)}\big)=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}\in\text{span}(W) $$
The “$\in\text{span}(W)$” holds because $W$ is the list of all the $u_j^{(i)}$ for $i=1,…,m$ and $j=1,…,n_i$. Hence $U_1+\dots+U_m\subset\text{span}(W)$.
In the other direction, let $w\in\text{span}(W)$. Then we can write $w$ as $w=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}$. Note that $\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}\in U_i$ since $U_i=\text{span}(u_1^{(i)},…,u_{n_i}^{(i)})$. Define $u_i\equiv\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}\in U_i$. Then
$$ w=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}=\sum_{i=1}^{m}u_i\in U_1+\dots+U_m $$
and $\text{span}(W)\subset U_1+\dots+U_m$. Hence $\text{span}(W)=U_1+\dots+U_m$. In other words
$$\begin{align*} U_1+\dots+U_m &\equiv \{u_1+\dots+u_m:u_1\in U_1,...,u_m\in U_m\}\\ &= \Big\{\sum_{j=1}^{n_1}a_j^{(1)}u_j^{(1)}+\dots+\sum_{j=1}^{n_m}a_j^{(m)}u_j^{(m)}:a_j^{(i)}\in\mathbb{F}\Big\}\\ &= \Big\{\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}:a_j^{(i)}\in\mathbb{F}\Big\}\\ &\equiv\text{span}(W) \end{align*}$$
Now let’s show that $\dim{(U_1+\dots+U_m)}=\text{len}(W)$ if and only if $W$ is linearly independent in $U_1+\dots+U_m$.
Suppose $W$ is linearly independent. Then $W$ spans and is linearly independent in $U_1+\dots+U_m$. Hence $W$ is a basis for $U_1+\dots+U_m$ and $\dim{(U_1+\dots+U_m)}=\text{len}(W)$.
In the other direction, suppose $\dim{(U_1+\dots+U_m)}=\text{len}(W)$. Since $\text{span}(W)=U_1+\dots+U_m$, we know, from 2.31 (p.40-41), that $W$ contains a basis for $U_1+\dots+U_m$. If $W$ is linearly dependent, then the Linear Dependence Lemma (2.21, p.34) tells us that $u_1^{(1)}=0$ or that at least one of the vectors in $W$ is in the span of the previous vectors. Then steps $1$ and $j$ from the proof of 2.31 will remove at least one vector from $W$ to get a basis $B$ for $U_1+\dots+U_m$. Then $\text{len}(W)\gt\text{len}(B)=\dim{(U_1+\dots+U_m)}$. Contradiction and $W$ is linearly independent.
Now let’s show that $W$ is linearly independent if and only if $U_1+\dots+U_m=U_1\oplus\dots\oplus U_m$ is a direct sum.
Suppose that $U_1+\dots+U_m$ is a direct sum and let $u\in U_1+\dots+U_m$. By the definition of direct sum, $u$ can be written in exactly one way as a sum $u=\sum_{i=1}^{m}u_i$ where $u_i\in U_i$. By 2.29 (p.39), $u_i$ can be written in exactly one way as a linear combination of the basis $u_1^{(i)},…,u_{n_i}^{(i)}$. That is, for some unique list of $a_j^{(i)}$’s, we have
$$ u=\sum_{i=1}^{m}u_i=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)} $$
In particular, for $u=0$, we have
$$ 0=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)} $$
Note that if we take $a_j^{(i)}=0$ for all $i$ and $j$, then this equation is satisfied. Again, these $0=a_j^{(i)}$’s are unique, which is to say that no other linear combination of the $u_j^{(i)}$’s will equal $0$. Hence $W$ is linearly independent in $U_1+\dots+U_m$.
In the other direction, suppose that $W$ is linearly independent and let $0=u_1+\dots+u_m$ for some $u_1\in U_1,…,u_m\in U_m$. Then $u_i=\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}$ for some $a_j^{(i)}\in\mathbb{F}$ and
$$ 0=\sum_{i=1}^{m}u_i=\sum_{i=1}^{m}\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)} $$
The linear independence of $W$ implies that $a_j^{(i)}=0$ for all $i$ and $j$. Hence $u_i=\sum_{j=1}^{n_i}a_j^{(i)}u_j^{(i)}=0$ for all $i$. By 1.44 (p.23), this implies that $U_1+\dots+U_m=U_1\oplus\dots\oplus U_m$ is a direct sum. $\wes$
Proposition App.11 <–> 3.43 <–> 10.4 Matrix Multiplication Suppose that $u\equiv u_1,\dots,u_p$ is a basis of $U$, that $v\equiv v_1,\dots,v_n$ is a basis of $V$, and that $w\equiv w_1,\dots,w_m$ is a basis of $W$. Let $T\in\linmap{U}{V}$ and $S\in\linmap{V}{W}$. Then
$$\align{ \mtrxof{ST,u,w} &= \mtrxof{S,v,w}\mtrxof{T,u,v}\tag{App.11.1} \\\\ &= \sum_{j=1}^n\mtrxof{S,v,w}_{:,j}\mtrxof{T,u,v}_{j,:}\tag{App.11.2} }$$
Proof Since $w=w_1,\dots,w_m$ is a basis of $W$, then there exist scalars $s_{i,j}$ for $i=1,\dots,m$ and $j=1,\dots,n$ such that
$$ Sv_j=\sum_{i=1}^ms_{i,j}w_i $$
Similarly there exist scalars $t_{j,k}$ for $j=1,\dots,n$ and $k=1,\dots,p$ such that
$$ Tu_k=\sum_{j=1}^nt_{j,k}v_j $$
Hence
$$ (ST)u_k=S(Tu_k)=S\Prn{\sum_{j=1}^nt_{j,k}v_j}=\sum_{j=1}^nt_{j,k}Sv_j=\sum_{j=1}^nt_{j,k}\sum_{i=1}^ms_{i,j}w_i=\sum_{j=1}^n\sum_{i=1}^ms_{i,j}t_{j,k}w_i=\sum_{i=1}^m\sum_{j=1}^ns_{i,j}t_{j,k}w_i $$
In particular
$$ (ST)u_1=\sum_{i=1}^m\sum_{j=1}^ns_{i,j}t_{j,1}w_i=\sum_{j=1}^ns_{1,j}t_{j,1}w_1+\dotsb+\sum_{j=1}^ns_{m,j}t_{j,1}w_m $$
and
$$ (ST)u_p=\sum_{i=1}^m\sum_{j=1}^ns_{i,j}t_{j,p}w_i=\sum_{j=1}^ns_{1,j}t_{j,p}w_1+\dotsb+\sum_{j=1}^ns_{m,j}t_{j,p}w_m $$
Hence
$$\align{ \mtrxof{S,v,w}\mtrxof{T,u,v} &= \pmtrx{\mtrxof{S,v,w}_{:,1}&\dotsb&\mtrxof{S,v,w}_{:,n}}\pmtrx{\mtrxof{T,u,v}_{:,1}&\dotsb&\mtrxof{T,u,v}_{:,p}} \\ &= \pmtrx{\mtrxof{Sv_1,w}&\dotsb&\mtrxof{Sv_n,w}}\pmtrx{\mtrxof{Tu_1,v}&\dotsb&\mtrxof{Tu_p,v}} \\ &= \pmtrx{s_{1,1}&\dotsb&s_{1,n}\\\vdots&\ddots&\vdots\\s_{m,1}&\dotsb&s_{m,n}}\pmtrx{t_{1,1}&\dotsb&t_{1,p}\\\vdots&\ddots&\vdots\\t_{n,1}&\dotsb&t_{n,p}} \\ &= \pmtrx{\sum_{j=1}^ns_{1,j}t_{j,1}&\dotsb&\sum_{j=1}^ns_{1,j}t_{j,p}\\\vdots&\ddots&\vdots\\\sum_{j=1}^ns_{m,j}t_{j,1}&\dotsb&\sum_{j=1}^ns_{m,j}t_{j,p}} \\ &= \pmtrx{\mtrxof{STu_1,w}&\dotsb&\mtrxof{STu_p,w}} \\ &= \pmtrx{\mtrxof{ST,u,w}_{:,1}&\dotsb&\mtrxof{ST,u,w}_{:,p}} \\ &= \mtrxof{ST,u,w} }$$
and
$$\align{ \mtrxof{S,v,w}\mtrxof{T,u,v} &= \pmtrx{\sum_{j=1}^ns_{1,j}t_{j,1}&\dotsb&\sum_{j=1}^ns_{1,j}t_{j,p}\\\vdots&\ddots&\vdots\\\sum_{j=1}^ns_{m,j}t_{j,1}&\dotsb&\sum_{j=1}^ns_{m,j}t_{j,p}} \\ &= \sum_{j=1}^n\pmtrx{s_{1,j}t_{j,1}&\dotsb&s_{1,j}t_{j,p}\\\vdots&\ddots&\vdots\\s_{m,j}t_{j,1}&\dotsb&s_{m,j}t_{j,p}} \\ &= \sum_{j=1}^n\pmtrx{s_{1,j}\\\vdots\\s_{m,j}}\pmtrx{t_{j,1}&\dotsb&t_{j,p}} \\ &= \sum_{j=1}^n\mtrxof{S,v,w}_{:,j}\mtrxof{T,u,v}_{j,:} }$$
$\wes$
Proposition App.12 <–> 10.5 Suppose $u\equiv u_1,\dots,u_n$ and $v\equiv v_1,\dots,v_n$ are bases of $V$. Then the matrices $\mtrxof{I,u,v}$ and $\mtrxof{I,v,u}$ are invertible (in the sense of 10.3, not 3.53) and
$$ \inv{\mtrxof{I,u,v}}=\mtrxof{I,v,u} \dq\dq \inv{\mtrxof{I,v,u}}=\mtrxof{I,u,v} $$
Proof App.11 gives
$$ \mtrxof{I,v,u}\mtrxof{I,u,v}=\mtrxof{II,u,u}=I_n \\ \mtrxof{I,u,v}\mtrxof{I,v,u}=\mtrxof{II,v,v}=I_n $$
$\wes$
Proposition App.13 Let $v_1,…,v_n$ be a basis for $V$ and let $T\in\lnmpsb(V,W)$. Then $T=0$ if and only if $Tv_k=0$ for $k=1,…,n$.
Proof If $T=0$, then $Tv_k=0$ for $k=1,…,n$. If $Tv_k=0$ for $k=1,…,n$ and $v=\sum_k^na_kv_k\in V$, then $Tv=\sum_k^na_kTv_k=0$. $\wes$
Proposition App.14 Let $v_1,…,v_n$ be a basis for $V$ and let $S,T\in\linmap{V}{W}$. Then $S=T$ if and only if $Sv_k=Tv_k$ for $k=1,…,n$.
Proof Note that
$$ S=T \iff S-T=0 \iff (S-T)v_k=0\text{ for }k=1,\dots,n \iff Sv_k=Tv_k\text{ for }k=1,\dots,n $$
where the second equivalence follows from App.13. $\wes$
App.15<–>Exercise 6.A.19 Suppose $V$ is a real inner product space. Then
$$ \innprd{u}{v}=\frac{\dnorm{u+v}^2-\dnorm{u-v}^2}{4} $$
for all $u,v\in V$.
Proof For any $u,v\in V$, we have
$$\begin{align*} \dnorm{u+v}^2 &= \innprd{u+v}{u+v} \\ &= \innprd{u}{u+v}+\innprd{v}{u+v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{v}{u}+\dnorm{v}^2 \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{u}{v}+\dnorm{v}^2 \\ &= \dnorm{u}^2+2\innprd{u}{v}+\dnorm{v}^2 \end{align*}$$
Similarly
$$\begin{align*} \dnorm{u-v}^2 &= \innprd{u-v}{u-v} \\ &= \innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{v}{u}+\dnorm{v}^2 \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{u}{v}+\dnorm{v}^2 \\ &= \dnorm{u}^2-2\innprd{u}{v}+\dnorm{v}^2 \end{align*}$$
Hence
$$ \frac{\dnorm{u+v}^2-\dnorm{u-v}^2}{4} = \frac{4\innprd{u}{v}}{4} = \innprd{u}{v} \quad\blacksquare $$
App.16<–>Exercise 6.A.20 Suppose $V$ is a complex inner product space. Then
$$ \innprd{u}{v}=\frac{\dnorm{u+v}^2-\dnorm{u-v}^2+\dnorm{u+iv}^2i-\dnorm{u-iv}^2i}{4} $$
for all $u,v\in V$.
Proof For any $u,v\in V$, we have
$$\begin{align*} \dnorm{u+v}^2 &= \innprd{u+v}{u+v} \\ &= \innprd{u}{u+v}+\innprd{v}{u+v} \\ &= \innprd{u}{u}+\innprd{u}{v}+\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2+\innprd{u}{v}+\innprd{v}{u}+\dnorm{v}^2 \\ \end{align*}$$
Similarly
$$\begin{align*} \dnorm{u-v}^2 &= \innprd{u-v}{u-v} \\ &= \innprd{u}{u-v}+\innprd{-v}{u-v} \\ &= \innprd{u}{u}+\innprd{u}{-v}+\innprd{-v}{u}+\innprd{-v}{-v} \\ &= \innprd{u}{u}-\innprd{u}{v}-\innprd{v}{u}+\innprd{v}{v} \\ &= \dnorm{u}^2-\innprd{u}{v}-\innprd{v}{u}+\dnorm{v}^2 \\ \end{align*}$$
Hence
$$ \dnorm{u+v}^2-\dnorm{u-v}^2 = 2\innprd{u}{v}+2\innprd{v}{u}\tag{App.16.1} $$
Next
$$\begin{align*} i\dnorm{u+iv}^2 &= i\innprd{u+iv}{u+iv} \\ &= i\innprd{u}{u+iv}+i\innprd{iv}{u+iv} \\ &= i\innprd{u}{u}+i\innprd{u}{iv}+i\innprd{iv}{u}+i\innprd{iv}{iv} \\ &= i\innprd{u}{u}+i\overline{i}\innprd{u}{v}+i^2\innprd{v}{u}+i^2\overline{i}\innprd{v}{v} \\ &= i\innprd{u}{u}+i(-i)\innprd{u}{v}-\innprd{v}{u}-(-i)\innprd{v}{v} \\ &= i\innprd{u}{u}-i^2\innprd{u}{v}-\innprd{v}{u}+i\innprd{v}{v} \\ &= i\dnorm{u}^2+\innprd{u}{v}-\innprd{v}{u}+i\dnorm{v}^2 \\ \end{align*}$$
Similarly
$$\begin{align*} i\dnorm{u-iv}^2 &= i\innprd{u-iv}{u-iv} \\ &= i\innprd{u}{u-iv}+i\innprd{-iv}{u-iv} \\ &= i\innprd{u}{u}+i\innprd{u}{-iv}+i\innprd{-iv}{u}+i\innprd{-iv}{-iv} \\ &= i\innprd{u}{u}+i(\overline{-i})\innprd{u}{v}+i(-i)\innprd{v}{u}+i(-i)(\overline{-i})\innprd{v}{v} \\ &= i\innprd{u}{u}+ii\innprd{u}{v}-i^2\innprd{v}{u}-i^2i\innprd{v}{v} \\ &= i\innprd{u}{u}-\innprd{u}{v}+\innprd{v}{u}+i\innprd{v}{v} \\ &= i\dnorm{u}^2-\innprd{u}{v}+\innprd{v}{u}+i\dnorm{v}^2 \\ \end{align*}$$
Hence
$$ i\dnorm{u+iv}^2-i\dnorm{u-iv}^2 = 2\innprd{u}{v}-2\innprd{v}{u}\tag{App.16.2} $$
Combining App.16.1 and App.16.2, we get
$$\begin{align*} \frac{\dnorm{u+v}^2-\dnorm{u-v}^2+\dnorm{u+iv}^2i-\dnorm{u-iv}^2i}{4} &= \frac{2\innprd{u}{v}+2\innprd{v}{u}+2\innprd{u}{v}-2\innprd{v}{u}}{4} \\ &= \frac{4\innprd{u}{v}}{4} \\ &= \innprd{u}{v} \end{align*}$$
$\wes$
Proposition App.17<–>3.69 Suppose $U$ and $V$ are finite-dimensional with $\dim{U}=\dim{V}$. Let $T\in\linmap{U}{V}$. Then the following are equivalent:
(a) $T$ is invertible
(b) $T$ is injective
(c) $T$ is surjective
Proof Suppose $T$ is invertible. Let $u_1,u_2\in U$ such that $Tu_1=Tu_2$. Then
$$ u_1=(\inv{T}T)u_1=\inv{T}(Tu_1)=\inv{T}(Tu_2)=(\inv{T}T)u_2=u_2 $$
Hence $T$ is injective and (a)$\implies$(b).
Suppose $T$ is injective. Then $\nullsp{T}=\set{0}$ (by 3.16) and hence $0=\dim{\nullsp{T}}$. From the Fundamental Theorem of Linear Maps (3.22), we have
$$ \dim{\rangsp{T}}=\dim{U}-\dim{\nullsp{T}}=\dim{V} $$
Hence $\rangsp{T}=V$ (by App.22) and (b)$\implies$(c).
Suppose $T$ is surjective so that $\rangsp{T}=V$. From the Fundamental Theorem of Linear Maps, we get
$$ \dim{\nullsp{T}}=\dim{U}-\dim{\rangsp{T}}=\dim{V}-\dim{V}=0 $$
Hence $\nullsp{T}=\set{0}$ and $T$ is injective. Since $T$ is surjective and injective, then 3.56 implies that $T$ is invertible. Hence (c)$\implies$(a). $\wes$
Proposition App.18<–>Exercise 3.D.9 Suppose $U$ and $V$ are finite-dimensional with $\dim{U}=\dim{V}$. And let $S\in\linmap{U}{V}$ and $T\in\linmap{V}{U}$. Then $ST\wiov$ is invertible if and only if both $S$ and $T$ are invertible.
Proof Suppose $ST$ is invertible. Then there exists $R\in\lnmpsb(V)$ such that $R(ST)=(ST)R=I_V$.
Let $v_1\in\mathscr{N}(T)\subset V$. Then
$$ v_1=I_Vv_1=R(ST)v_1=(RS)Tv_1=(RS)0=0 $$
Hence $\mathscr{N}(T)=\{0\}$ and $T$ is injective. Then App.17 gives that $T$ is invertible.
Let $v_2\in V$. Then
$$ v_2=I_Vv_2=(ST)Rv_2=S(TR)v_2\in\mathscr{R}(S) $$
Hence $V\subset\rangsp{S}$, hence $V=\rangsp{S}$, and hence $S$ is surjective. Then App.17 gives that $S$ is invertible.
Conversely, suppose $S$ and $T$ are both invertible. Then
$$ (ST)(T^{-1}S^{-1})=S(TT^{-1})S^{-1}=SI_US^{-1}=SS^{-1}=I_V $$
and
$$ (T^{-1}S^{-1})(ST)=T^{-1}(S^{-1}S)T=T^{-1}I_UT=T^{-1}T=I_V $$
Hence $T^{-1}S^{-1}$ satisfies the properties required for an inverse of $ST$. Hence $ST$ is invertible and $(ST)^{-1}=T^{-1}S^{-1}$. $\wes$
Proposition App.19<–>Exercise 3.D.10 Suppose $U$ and $V$ are finite-dimensional with $\dim{U}=\dim{V}$. And let $S\in\linmap{U}{V}$ and $T\in\linmap{V}{U}$. Then $ST=I_V$ if and only if $TS=I_U$.
Proof Suppose $ST=I_V$. Note that $I_V$ is invertible ($I_V^{-1}=I_V$ because $I_VI_V=I_V$). Hence $ST$ is invertible. Then App.18 implies that both $S$ and $T$ are invertible. Multiplying both sides of $ST=I_V$ by $T^{-1}$ on the right, we get
$$ S=STT^{-1}=I_VT^{-1}=T^{-1} $$
Now multiply both sides of this equation by $T$ on the left:
$$ TS=TT^{-1}=I_U $$
Conversely, we can simply reverse the roles of $S$ and $T$ and walk through the same steps. $\wes$
Proposition App.20 Let $T\wiov$. Then $T=I$ if and only if $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$.
Proof First suppose that $T=I$. Then, for all $u,v\in V$, we have
$$ \innprd{Tu}{v}=\innprd{Iu}{v}=\innprd{u}{v} $$
Conversely, suppose that $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$. Fix $u\in V$. Then, for all $v\in V$, we have
$$ \innprd{Iu}{v}=\innprd{u}{v}=\innprd{Tu}{v} $$
Hence, for all $v\in V$, we have
$$ 0=\innprd{Tu}{v}-\innprd{Iu}{v}=\innprd{Tu-Iu}{v} $$
In particular, put $v\equiv Tu-Iu$. Then
$$ 0=\innprd{Tu-Iu}{Tu-Iu} $$
By the definiteness of an inner product, we get $Tu-Iu=0$. Since $u$ was chosen arbitrarility, then $Tu-Iu=0$ all of $u\in V$. $\wes$
Proposition App.21 Let $T\wiov$ and let $e_1,\dots,e_n$ be a basis of $V$. Then $T=I$ if and only if $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$.
Proof By App.20, it suffices to show that $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$ if and only if $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$.
First suppose that $\innprd{Tu}{v}=\innprd{u}{v}$ for all $u,v\in V$. Then $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$.
Conversely, suppose that $\innprd{Te_j}{e_k}=\innprd{e_j}{e_k}$ for all $j,k=1,\dots,n$. Then
$$ \innprd{Tu}{v}=\innprdBg{T\Prn{\sum_{j=1}^nu_je_j}}{\sum_{k=1}^nv_ke_k}=\innprdBg{\sum_{j=1}^nu_jTe_j}{\sum_{k=1}^nv_ke_k}=\sum_{j=1}^n\sum_{k=1}^nu_i\cj{v_i}\innprd{Te_j}{e_k}=\sum_{j=1}^n\sum_{k=1}^nu_i\cj{v_i}\innprd{e_j}{e_k}=\innprd{u}{v} $$
$\wes$
Proposition App.22 Suppose $V$ is finite-dimensional and $U$ is a subspace of $V$. Then $\dim{V}=\dim{U}$ if and only if $V=U$.
Proof Suppose $\dim{V}=\dim{U}$. Let $u_1,…,u_n$ be a basis for $U$. Then $n=\dim{U}=\dim{V}$ and $u_1,…,u_n\in V$. By 2.39 (p.45), $u_1,…,u_n$ is a basis for $V$. Hence $V=\text{span}(u_1,…,u_n)=U$.
In the other direction, suppose $V=U$. Then $\dim{V}=\dim{U}$. $\wes$
Proposition App.23 Suppose $v_1,\dots,v_n$ is an orthogonal list - each vector is orthogonal to all the other vectors in the list. Let $e_1,\dots,e_n$ be the result of applying Gram-Schmidt to $v_1,\dots,v_n$. Then
$$ e_j = \frac{v_j}{\dnorm{v_j}} $$
for $j=1,\dots,n$.
Proof By definition, $e_1\equiv v_1\big/\dnorm{v_1}$. And since
$$ \innprd{v_2}{e_1} = \innprdBg{v_2}{\frac{v_1}{\dnorm{v_1}}} = \cj{\Prn{\frac1{\dnorm{v_1}}}}\innprd{v_2}{v_1}=0 $$
then
$$ e_2 = \frac{v_2-\innprd{v_2}{e_1}e_1}{\dnorm{v_2-\innprd{v_2}{e_1}e_1}} = \frac{v_2}{\dnorm{v_2}} $$
Let $j\in{3,\dots,n}$. Our induction assumption is that $e_k=v_k\big/\dnorm{v_k}$ for any $k=1,\dots,j-1$. Hence, for any $k=1,\dots,j-1$, we have
$$ \innprd{v_j}{e_k} = \innprdBg{v_j}{\frac{v_k}{\dnorm{v_k}}} = \cj{\Prn{\frac1{\dnorm{v_k}}}}\innprd{v_j}{v_k}=0 $$
Hence
$$ e_j = \frac{v_j-\sum_{k=1}^{j-1}\innprd{v_j}{e_k}e_k}{\dnorm{v_j-\sum_{k=1}^{j-1}\innprd{v_j}{e_k}e_k}} = \frac{v_j}{\dnorm{v_j}} $$
$\wes$
Proposition App.24<–>Exercise 6.C.1 Suppose $v_1,\dots,v_m\in V$. Then
$$ \cbr{v_1,\dots,v_m}^\perp=\prn{\span{v_1,\dots,v_m}}^\perp $$
Proof Let $u\in\cbr{v_1,\dots,v_m}^\perp$. And let $v\in\span{v_1,\dots,v_m}$. Then
$$\begin{align*} \innprd{u}{v} = \innprdBg{u}{\sum_{j=1}^ma_jv_j} = \sum_{j=1}^m\innprd{u}{a_jv_j} = 0 \end{align*}$$
The last equality holds because $u$ is orthogonal to each of the $v_1,\dots,v_m$ and scaling preserves orthogonality. Hence $u\in\prn{\span{v_1,\dots,v_m}}^\perp$ and $\cbr{v_1,\dots,v_m}^\perp\subset\prn{\span{v_1,\dots,v_m}}^\perp$.
In the other direction, let $v\in\prn{\span{v_1,\dots,v_m}}^\perp$ and let $v_k\in\cbr{v_1,\dots,v_m}$. Then $v_k\in\span{v_1,\dots,v_m}$. Hence $v$ is orthogonal to $v_k$ and $\prn{\span{v_1,\dots,v_m}}^\perp\subset\cbr{v_1,\dots,v_m}^\perp$. $\wes$
Proposition App.25 Suppose $V$ and $W$ are finite-dimensional with $\dim{V}=\dim{W}$. Then $S\in\linmap{V}{W}$ is an isometry if and only if, for any orthonormal bases $\epsilon$ of $V$ and $\varphi$ of $W$, the columns and rows of $\mtrxof{S,\epsilon,\varphi}$ are orthonormal with respect the usual dot product $\innprd{\cdot}{\cdot}_{\wF^n}$ of $\wF^n$.
Proof Put $n\equiv\dim{V}=\dim{W}$. Let $e\equiv e_1,\dots,e_n$ be an orthonormal basis of $V$ and let $f\equiv f_1,\dots,f_n$ be orthonormal basis of $W$.
First suppose that $S$ is an isometry. Note that 6.30 gives
$$ Se_k=\sum_{i=1}^n\innprd{Se_k}{f_i}_Wf_i $$
Then
$$\align{ \mtrxof{S,e,f} &= \pmtrx{\mtrxof{S,e,f}_{:,1}&\dotsb&\mtrxof{S,e,f}_{:,n}} \\ &= \pmtrx{\mtrxof{Se_1,f}&\dotsb&\mtrxof{Se_n,f}} \\ &= \pmtrx{\innprd{Se_1}{f_1}_W&\dotsb&\innprd{Se_n}{f_1}_W\\\vdots&\ddots&\vdots\\\innprd{Se_1}{f_n}_W&\dotsb&\innprd{Se_n}{f_n}_W} \\ }$$
and
$$\align{ \innprdbg{\mtrxof{S,e,f}_{:,j}}{\mtrxof{S,e,f}_{:,k}}_{\wF^n} &= \sum_{i=1}^n\innprd{Se_j}{f_i}_W\cj{\innprd{Se_k}{f_i}_W} \\ &= \sum_{i=1}^n\innprdbg{Se_j}{\innprd{Se_k}{f_i}_Wf_i}_W \\ &= \innprdBgg{Se_j}{\sum_{i=1}^n\innprd{Se_k}{f_i}_Wf_i}_W \\ &= \innprd{Se_j}{Se_k}_W\tag{by 6.30} \\ &= \cases{1&j=k\\0&j\neq k} }$$
The last equality holds because $Se_1,\dots,Se_n$ is orthonormal (by App.5(c)). Hence the columns of $\mtrxof{S,e,f}$ are orthonormal with respect to $\innprd{\cdot}{\cdot}_{\wF^n}$. Also note that $Se_1,\dots,Se_n$ is an orthonormal basis of $W$ since $n=\dim{W}$ (by 6.28). Hence
$$\align{ \innprdbg{\mtrxof{S,e,f}_{j,:}}{\mtrxof{S,e,f}_{k,:}}_{\wF^n} &= \sum_{i=1}^n\innprd{Se_i}{f_j}_W\cj{\innprd{Se_i}{f_k}_W} \\ &= \sum_{i=1}^n\cj{\innprd{f_j}{Se_i}_W}\innprd{f_k}{Se_i}_W \\ &= \sum_{i=1}^n\innprdbg{f_k}{\innprd{f_j}{Se_i}_WSe_i}_W \\ &= \innprdBgg{f_k}{\sum_{i=1}^n\innprd{f_j}{Se_i}_WSe_i}_W \\ &= \innprd{f_k}{f_j}_W\tag{by 6.30} \\ &= \cases{1&j=k\\0&j\neq k} }$$
Hence the rows of $\mtrxof{S,e,f}$ are orthonormal with respect to $\innprd{\cdot}{\cdot}_{\wF^n}$.
Conversely, suppose that, for any orthonormal bases $\epsilon$ of $V$ and $\varphi$ of $W$, the columns and rows of $\mtrxof{S,\epsilon,\varphi}$ are orthonormal with respect $\innprddt_{\wF^n}$. Then
$$\align{ \mtrxof{\adjt{S}S,e,e} &= \mtrxof{\adjt{S},f,e}\mtrxof{S,e,f}\tag{by App.11} \\ &= \adjt{\mtrxof{S,e,f}}\mtrxof{S,e,f}\tag{by App.4} \\ &= I_n\tag{by App.26} \\ &= \mtrxof{I_V,e,e} }$$
Since $\mtrxof{\cdot,e,e}$ is an isomorphism (by 3.60), then it’s injective (by 3.56). Hence $\adjt{S}S=I_V$ and $S$ is an isometry (by App.5(e)). $\wes$
Proposition App.26 Let $U\in\wF^{m\times n}$. Then the columns of $U$ are orthonormal if and only if $\adjt{U}U=I_n$.
Note that $U$ need not be square for this to hold.
Proof Suppose the columns of $U$ are orthonormal. Then
$$ \innprd{u_{:,j}}{u_{:,k}}=\cases{1&j=k\\0&j\neq k} $$
and
$$\align{ \adjt{U}U &= \pmtrx{\cj{u_{1,1}}&\dotsb&\dotsb&\cj{u_{m,1}}\\\vdots&\ddots&\ddots&\vdots\\\cj{u_{1,n}}&\dotsb&\dotsb&\cj{u_{m,n}}}\pmtrx{u_{1,1}&\dotsb&u_{1,n}\\\vdots&\ddots&\vdots\\\vdots&\ddots&\vdots\\u_{m,1}&\dotsb&u_{m,n}} \\\\ &= \pmtrx{\sum_{j=1}^m\cj{u_{j,1}}u_{j,1}&\dotsb&\sum_{j=1}^m\cj{u_{j,1}}u_{j,n} \\ \vdots&\ddots&\vdots \\ \sum_{j=1}^m\cj{u_{j,n}}u_{j,1}&\dotsb&\sum_{j=1}^m\cj{u_{j,n}}u_{j,n} } \\\\ &= \pmtrx{\sum_{j=1}^mu_{j,1}\cj{u_{j,1}}&\dotsb&\sum_{j=1}^mu_{j,n}\cj{u_{j,1}} \\ \vdots&\ddots&\vdots \\ \sum_{j=1}^mu_{j,1}\cj{u_{j,n}}&\dotsb&\sum_{j=1}^mu_{j,n}\cj{u_{j,n}} } \\\\ &= \pmtrx{\innprd{u_{:,1}}{u_{:,1}}&\dotsb&\innprd{u_{:,n}}{u_{:,1}} \\ \vdots&\ddots&\vdots \\ \innprd{u_{:,1}}{u_{:,n}}&\dotsb&\innprd{u_{:,n}}{u_{:,n}} } \\\\ &= I_n }$$
Conversely, suppose that $\adjt{U}U=I_n$. Then
$$ I_n=\adjt{U}U =\pmtrx{\cj{u_{1,1}}&\dotsb&\dotsb&\cj{u_{m,1}}\\\vdots&\ddots&\ddots&\vdots\\\cj{u_{1,n}}&\dotsb&\dotsb&\cj{u_{m,n}}}\pmtrx{u_{1,1}&\dotsb&u_{1,n}\\\vdots&\ddots&\vdots\\\vdots&\ddots&\vdots\\u_{m,1}&\dotsb&u_{m,n}} = \pmtrx{\innprd{u_{:,1}}{u_{:,1}}&\dotsb&\innprd{u_{:,n}}{u_{:,1}} \\ \vdots&\ddots&\vdots \\ \innprd{u_{:,1}}{u_{:,n}}&\dotsb&\innprd{u_{:,n}}{u_{:,n}} } $$
Hence
$$ \innprd{u_{:,j}}{u_{:,k}}=\cases{1&j=k\\0&j\neq k} $$
Hence the columns of $U$ are orthonormal. $\wes$
Proposition App.27 Let $T\wiov$. Then, for any orthonormal basis $e$ of $V$ and for any $v\in V$, we have
$$ \adjt{\mtrxof{v,e}}\mtrxof{T,e}\mtrxof{v,e} = \innprd{Tv}{v} $$
Proof For any orthonormal basis $e\equiv e_1,\dots,e_n$ of $V$ and any $v\in V$, 6.30 gives
$$ Tv=\sum_{j=1}^n\innprd{Tv}{e_j}e_j \dq\text{and}\dq v=\sum_{j=1}^n\innprd{v}{e_j}e_j $$
Hence, for any orthonormal basis $e\equiv e_1,\dots,e_n$ of $V$ and any $v\in V$, we have
$$\align{ \adjt{\mtrxof{v,e}}\mtrxof{T,e}\mtrxof{v,e} &= \adjt{\mtrxof{v,e}}\mtrxof{T,e,e}\mtrxof{v,e} \\ &= \adjt{\mtrxof{v,e}}\mtrxof{Tv,e}\tag{by App.29} \\ &= \adjt{\pmtrx{\innprd{v}{e_1}\\\vdots\\\innprd{v}{e_n}}}\pmtrx{\innprd{Tv}{e_1}\\\vdots\\\innprd{Tv}{e_n}} \\ &= \pmtrx{\cj{\innprd{v}{e_1}}&\dotsb&\cj{\innprd{v}{e_n}}}\pmtrx{\innprd{Tv}{e_1}\\\vdots\\\innprd{Tv}{e_n}} \\ &= \sum_{j=1}^n\cj{\innprd{v}{e_j}}\innprd{Tv}{e_j} \\ &= \sum_{j=1}^n\innprdbg{Tv}{\innprd{v}{e_j}e_j} \\ &= \innprdBgg{Tv}{\sum_{j=1}^n\innprd{v}{e_j}e_j} \\ &= \innprd{Tv}{v} }$$
$\wes$
Proposition App.28 $T\wiov$ is positive if and only if $\mtrxof{T,e}$ is positive semi-definite for every orthonormal basis $e$ of $V$.
Proof Suppose $T$ is positive so that $\innprd{Tv}{v}\geq0$ for all $v\in V$ and $\adjtT=T$. Then App.27 gives
$$ \adjt{\mtrxof{v,e}}\mtrxof{T,e}\mtrxof{v,e} = \innprd{Tv}{v} \geq 0 $$
for any orthonormal basis $e$ of $V$ and any $v\in V$. And App.4 gives $\adjt{\mtrxof{T,e}}=\mtrxof{\adjtT,e}=\mtrxof{T,e}$ for any orthonormal basis $e$ of $V$. Hence $\mtrxof{T,e}$ is positive semi-definite for every orthonormal basis $e$ of $V$.
Conversely, suppose $\mtrxof{T,e}$ is positive semi-definite for every orthonormal basis $e$ of $V$. Hence, for every orthonormal basis $e$ of $V$, we have $\adjt{\mtrxof{v,e}}\mtrxof{T,e}\mtrxof{v,e}\geq 0$ and $\adjt{\mtrxof{T,e}}=\mtrxof{T,e}$. Then App.27 gives
$$ \innprd{Tv}{v} = \adjt{\mtrxof{v,e}}\mtrxof{T,e}\mtrxof{v,e} \geq 0 $$
for all $v\in V$. And App.4 gives $\mtrxof{\adjtT,e}=\adjt{\mtrxof{T,e}}=\mtrxof{T,e}$. By 3.60, $\mtrxof{\cdot,e}$ is an isomorphism. Hence it’s injective (by 3.56) and $\adjtT=T$. $\wes$
Proposition App.29 <–> 3.65 Suppose $v\equiv v_1,\dots,v_n$ is a basis of $V$ and $w\equiv w_1,\dots,w_m$ is a basis of $W$. Let $T\in\linmap{V}{W}$. Then, for any $u\in V$, we have
$$ \mtrxof{Tu,w}=\mtrxof{T,v,w}\mtrxof{u,v} $$
Proof Let $u\in V$. Then $u=\sum_{j=1}^nu_iv_i$ for some scalars $u_1,\dots,u_n\in\wF$. Then 3.62 gives
$$ \mtrxof{u,v}=\pmtrx{u_1\\\vdots\\u_n} $$
We also have
$$ Tu=T\Prn{\sum_{j=1}^nu_jv_j}=\sum_{j=1}^nu_jTv_j $$
Hence
$$\align{ \mtrxof{Tu,w} &= \mtrxofB{\sum_{j=1}^nu_jTv_j,w} \\ &= \sum_{j=1}^nu_j\mtrxof{Tv_j,w}\tag{by 3.36 and 3.38} \\ &= \sum_{j=1}^nu_j\mtrxof{T,v,w}_{:,j} \\ &= \mtrxof{T,v,w}\mtrxof{u,v}\tag{by 3.52} }$$
$\wes$